14.6: Вправа

Last updated
Save as PDF

Page ID: 66200

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Навички

Лічильна дошка і обладнання

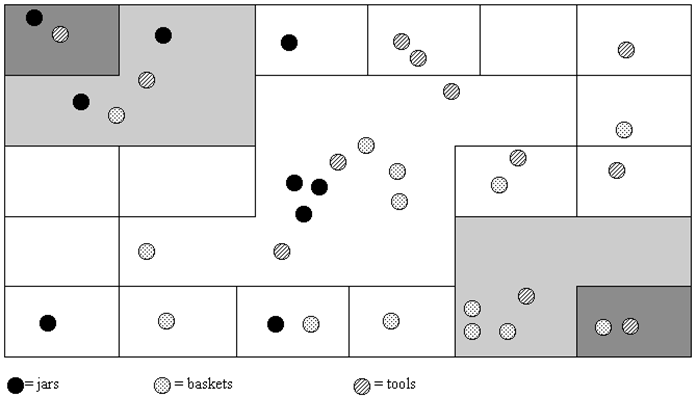
1) У наступній перуанській лічильній дошці визначте, скільки кожного предмета представлено. Будь ласка, покажіть всі ваші розрахунки разом з якимось поясненням того, як ви отримали свою відповідь. Зверніть увагу на клавішу внизу креслення.

$clipboard_e0c3bd0462129b752dac84432aaa0118a.png$

2) Намалюйте кіпу основним шнуром, який має гілки (шнури H), які показують на них кожне з наступних чисел. (Слід зробити один креслення для цієї проблеми зі шнуром для частини а зліва і рухаючись вправо для деталей b через d.)

а. 232	б. 5065
c. 23451	д. 3002

Базові базові конверсії

3) 423 в базі 5 до основи 10	4) 3044 в базі 5 до основи 10
5) 387 в базі 10 до основи 5	6) 2546 в базі 10 до бази 5
7) 110101 в базі 2 до основи 10	8) 11010001 в базі 2 до основи 10
9) 100 в базі 10 до основи 2	10) 2933 в базі 10 до основи 2
11) Перетворіть 653 в базу 7 на базу 10	12) Перетворіть 653 в базу 10 на базу 7
13) 3412 в базі 5 до основи 2	14) 10011011 в базі 2 до основи 5

(Підказка: спочатку перетворити на базу 10, а потім на кінцеву бажану базу)

Система Кайдоз

Припустимо, ви повинні були виявити стародавню систему базою-12, що складається з дванадцяти символів. Назвемо цю базову систему системою Кайдоз. Ось символи для кожного з чисел від 0 до 12:

$clipboard_ee37224e1a84172c879dd825a1675837c.png$

Перетворіть кожне з наступних чисел у Caidoz на базу 10

$clipboard_efb90ded3a486be54e3f82dbd093b307f.png$

C Перетворіть на наступні базові 10 чисел в Кайдоз, використовуючи символи, які виграли вище.

19) 175	20) 3030
21) 10000	22) 5507

Майя Конверсії

Перетворіть наступні числа в позначення майя. Покажіть свої розрахунки, які використовуються для отримання відповідей.

23) 135	24) 234
25) 360	26) 1215
27) 10500	28) 110000

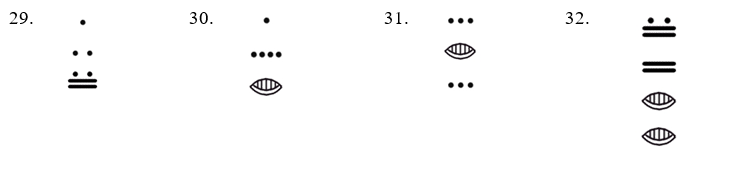
Перетворіть наступні числа майя в десяткові (база -10) чисел. Показати всі розрахунки.

$clipboard_e8eebd940665c72ab21363bb7b9f6bc50.png$

Джеймс Бідвелл припустив, що додавання майя було зроблено шляхом «просто об'єднання барів і точок і перенесення на наступне вище місце». Він продовжує говорити: «Після об'єднання точок і барів другим кроком є обмін кожні п'ять точок на один бар в тому ж положенні». Після перетворення наступних базових чисел 10 у вертикальні позначення майя (в базі 20, звичайно), виконайте зазначене додавання:

33) 32 + 11	34) 82 + 15
35) 35 + 148	36) 2412 + 5000
37) 450 + 844	38) 10000 + 20000
39) 4500 + 3500	40) 130000 + 30000

41) Використовуйте той факт, що майя мали систему числення база-20, щоб заповнити наступну таблицю множення. Записи таблиці повинні бути в позначеннях майя. Пам'ятайте: їх нуль виглядав так... Ксерокс, а потім виріжте таблицю нижче, заповніть її і вставте на домашнє завдання, якщо ви не хочете дублювати таблицю лінійкою.

(Думати, але не писати: Бідвелл стверджує, що для «множення майя потрібні лише ці записи». Що він має на увазі?)

Двійкові та шістнадцяткові

Сучасні комп'ютери працюють в світі електронних перемикачів «увімкнено» і «вимкнено», тому використовують двійкову систему підрахунку — базу 2, що складається всього з двох цифр: 0 і 1.

Перетворіть наступні двійкові числа в десяткові (основа -10) числа.

42) 1001	43) 101
4) 11010	45) 101110

Перетворіть наступні числа base-10 в двійкові

46) 7	47) 12
48) 36	49) 27

Чотири двійкові цифри разом можуть представляти будь-яке базове число 10 від 0 до 15. Для створення більш зрозумілого для людини подання двійково-закодованих чисел зазвичай використовуються шістнадцяткові числа, основа 16. Замість того, щоб використовувати 8,13,12 ₁₆ позначення, використане раніше, буква A використовується для представлення цифри 10, B для 11, до F для 15, тому 8,13,12 ₁₆ буде записано як 8DC.

Перетворіть наступні шістнадцяткові числа в десяткові (основа -10) числа.

50) С3	51) 4Д
52) 3А6	53) БС2

Перетворіть наступні числа бази-10 на шістнадцяткові

54) 152	55) 176
56) 2034	57) 8263

Розвідка

58) Які переваги і недоліки підстав крім десяти.

59) Передбачається, що вам покладено відповідальність за створення системи числення base-15. Які символи ви б використовувати для вашої системи і чому? Поясніть принаймні двома конкретними прикладами, як ви конвертуєте між вашою базовою системою 15 та десятковою системою.

60) Опишіть цікавий аспект цивілізації майя, який ми не обговорювали на уроці. Ваші висновки повинні надходити з якогось джерела, наприклад, енциклопедії статті або інтернет-сайту, і ви повинні надати посилання (і) на матеріали, які ви використовували (або публікаційну інформацію, або адресу в Інтернеті).

61) Для племені Папуасів на південному сході Нової Гвінеї потрібно було перевести біблійний уривок Іоанна 5:5 «І там був якийсь чоловік, який мав неміч 30 і 8 років» на «Людина лежала хвора одна людина, обидві руки, п'ять і три роки». Грунтуючись на власному розумінні базових систем (і деякого здорового глузду), надайте пояснення перекладу. Будь ласка, використовуйте повні речення, щоб зробити це. (Підказка: Щоб вирішити цю проблему, я прошу вас подумати про те, як працюють базові системи, звідки вони беруться, і як вони використовуються. Ви не обов'язково знайдете «відповідь» в читаннях або таких... вам доведеться продумати це і придумати розумну відповідь. Тільки переконайтеся, що вам чітко пояснити, чому уривок був перекладений так, як він був.)

62) Календар майя багато в чому обговорювався до грудня 2012 року. Дослідіть, як працює календар майя, і як підрахунки пов'язані з числом, яке вони використовують.