6.3: Найкоротший шлях

Last updated
Save as PDF

Page ID: 66244

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Коли ви відвідуєте веб-сайт, як Google Maps, або використовуєте свій смартфон, щоб запитати вказівки від дому до будинку вашої тітки в Пасадені, ви зазвичай шукаєте найкоротший шлях між двома місцями. Ці комп'ютерні програми використовують зображення карт вулиць як графіки, з розрахунковим часом водіння як ваги краю.

Хоча часто можна знайти найкоротший шлях на маленькому графіку шляхом вгадування та перевірки, наша мета в цьому розділі - розробити методи систематичного вирішення складних завдань за допомогою алгоритмів. Алгоритм - покрокова процедура вирішення проблеми. Алгоритм Дейкстри (вимовляється dike-stra) знайде найкоротший шлях між двома вершинами.

Алгоритм Дейкстри

Відзначте кінцеву вершину з відстанню в нуль. Позначити цю вершину як поточну.
Знайти всі вершини, що ведуть до поточної вершини. Розрахуйте їх відстані до кінця. Оскільки ми вже знаємо відстань поточної вершини від кінця, це просто зажадає додавання останнього ребра. Не записуйте цю відстань, якщо вона довша за раніше записану відстань.
Позначити поточну вершину як відвідану. Ми більше ніколи не будемо дивитися на цю вершину.
Позначте вершину з найменшою відстанню як поточну, і повторіть з кроку 2.

Приклад 3

Припустимо, вам потрібно подорожувати з Такома, штат Вашингтон (вершина T) до Якіми, штат Вашингтон (вершина Y). Дивлячись на карту, схоже на проїзд через Оберн (A), тоді гора Реньє (MR) може бути найкоротшою, але це не зовсім зрозуміло, оскільки ця дорога, ймовірно, повільніше, ніж проїзд на головному шосе через Північний Бенд (NB). Графік з часом в дорозі в хвилинах наведено нижче. Також показаний альтернативний маршрут через Eatonville (E) та Packwood (P).

$gt12.svg$

Рішення

$gt13.svg$ Крок 1: Відзначте кінцеву вершину з відстанню нуля. Відстані будуть записані в [дужках] після назви вершини.

$gt14.svg$ Крок 2: Для кожної вершини, що веде до Y, обчислюємо відстань до кінця. Наприклад, NB - це відстань 104 від кінця, а МР - 96 від кінця. Пам'ятайте, що відстані в даному випадку відносяться до часу в дорозі в хвилинах.

Крок 3 і 4: Ми позначимо Y як відвідувану, і відзначаємо вершину з найменшою записаною відстанню як поточну. У цей момент P буде позначено струмом. Повернутися до кроку 2.

$gt15.svg$ Крок 2 (#2): Для кожної вершини, що веде до P (і не веде до відвіданої вершини) знаходимо відстань від кінця. Оскільки Е 96 хвилин від P, і ми вже обчислили P 76 хвилин від Y, ми можемо обчислити, що E 96+76 = 172 хвилин від Y.

Якщо ми зробимо однакові обчислення для MR, ми обчислимо 76+27 = 103. Оскільки це більше, ніж раніше записане відстань від Y до MR, ми не будемо його замінювати.

Крок 3 і 4 (#2): Ми відзначаємо P як відвідувану і позначаємо вершину з найменшою записаною відстанню як поточну: MR. Назад до кроку 2.

$gt16.svg$ Крок 2 (#3): Для кожної вершини, що веде до MR (і не веде до відвідуваної вершини) ми знаходимо відстань до кінця. Єдиною вершиною, яку слід вважати, є A, оскільки ми вже відвідали Y та P. Додавання відстані MR 96 до довжини від A до MR дає відстань 96+79 = 175 хвилин від A до Y.

Крок 3 і 4 (#3): Ми позначаємо MR як відвідуваний і позначаємо вершину з найменшою записаною відстанню як поточну: NB. Повернутися до кроку 2.

$gt17.svg$ Крок 2 (#4): Для кожної вершини, що веде до NB, знаходимо відстань до кінця. Ми знаємо найкоротшу відстань від NB до Y - 104, а відстань від А до NB - 36, тому відстань від А до Y через NB становить 104+36 = 140. Оскільки ця відстань коротше, ніж раніше розраховане відстань від Y до A через MR, замінюємо його.

Крок 3 і 4 (#4): Ми відзначаємо NB як відвідуваний і позначаємо A як струм, оскільки тепер він має найкоротшу відстань.

$gt18.svg$ Крок 2 (#5): T - єдина невідвідувана вершина, що веде до A, тому обчислюємо відстань від T до Y через A: 20+140 = 160 хвилин.

Крок 3 і 4 (#5): Ми позначаємо A як відвідуваний і позначаємо E як поточний.

Крок 2 (#6): Єдина невідвідувана вершина, що веде до E, це T. Обчислення відстані від T до Y до E, обчислюємо$172+57 = 229$ хвилини. Оскільки це довше існуючого зазначеного часу, ми його не замінюємо.

Крок 3 (#6): Ми відзначаємо E як відвідуваний. Оскільки всі вершини були відвідані, ми зробили.

З цього ми знаємо, що найкоротший шлях від Такоми до Якіми займе 160 хвилин. Відстежуючи, яка послідовність ребер дала 160 хвилин, ми бачимо найкоротший шлях T-A-NB-Y.

Алгоритм Дейкстри є оптимальним алгоритмом, тобто він завжди створює найкоротший шлях, а не лише шлях, який є досить коротким, за умови його існування. Цей алгоритм також ефективний, а це означає, що він може бути реалізований за розумний проміжок часу. Алгоритм Дейкстри займає близько V ² обчислень, де V - кількість вершин у графі [1]. Графік з вершинами 100 займе близько 10 000 обчислень. Хоча це було б багато зробити вручну, це не так багато для комп'ютера, щоб впоратися. Саме завдяки такій ефективності GPS-пристрій вашого автомобіля може обчислити напрямки руху всього за кілька секунд.

На відміну від цього, неефективний алгоритм може спробувати перерахувати всі можливі шляхи, а потім обчислити довжину кожного шляху. Спроба перерахувати всі можливі шляхи може легко прийняти 10 ²⁵ обчислень, щоб обчислити найкоротший шлях лише з 25 вершинами; це 1 з 25 нулями після нього! Щоб поставити це в перспективі, найшвидший комп'ютер у світі все одно витрачав би більше 1000 років, аналізуючи всі ці шляхи.

Приклад 4

Судноплавна компанія повинна направити пакет з Вашингтона, округ Колумбія, до Сан-Дієго, Каліфорнія. Щоб мінімізувати витрати, пакет спочатку буде відправлений до їх процесингового центру в Балтіморі, штат Меріленд, а потім відправляється в рамках масових поставок між їх різними процесинговими центрами, в кінцевому підсумку в їх обробному центрі в Бейкерсфілді, штат Каліфорнія. Звідти він буде доставлений на невеликій вантажівці в Сан-Дієго.

Час в дорозі, в годині, між їх обробними центрами наведено в таблиці нижче. Три години було додано до кожного часу поїздки для обробки. Знайдіть найкоротший шлях від Балтімора до Бейкерсфілда. 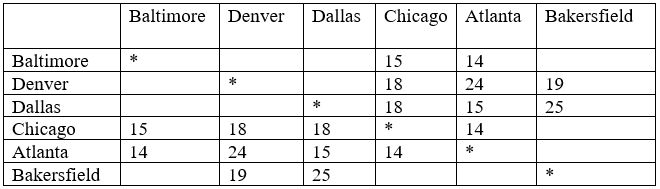$clipboard_e41f1a50ddf89a90a45a6f95a35f9da9f.png$

Рішення

Хоча ми могли б намалювати графік, ми також можемо працювати безпосередньо з таблиці.

Крок 1: Кінцева вершина, Бейкерсфілд, позначена як поточна.

Крок 2: Усі міста, підключені до Бейкерсфілда, в даному випадку Денвер і Даллас, розраховують відстані; ми позначимо ці відстані в заголовках стовпців.

Крок 3 та 4: Марк Бейкерсфілд як відвідав. Тут ми робимо це, затінюючи відповідний рядок і стовпець таблиці. Відзначаємо Денвер як поточний, показаний жирним шрифтом, так як це вершина з найкоротшою відстанню.

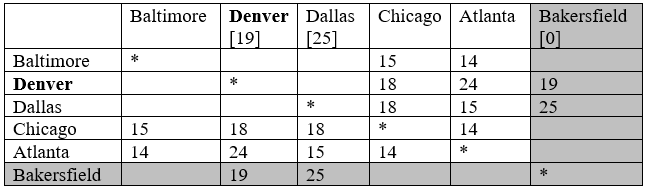
$clipboard_e759bf79d3d787956ad0bf4fcda7511b5.png$

Крок 2 (#2): Для міст, підключених до Денвера, розрахуйте відстань до кінця. Наприклад, Чикаго - 18 годин від Денвера, а Денвер - 19 годин від кінця, відстань для Чикаго до кінця - 18+19 = 37 (від Чикаго до Денвера до Бейкерсфілда). Атланта знаходиться 24 години від Денвера, тому відстань до кінця становить 24+19 = 43 (від Атланти до Денвера до Бейкерсфілда).

Крок 3 і 4 (#2): Ми відзначаємо Денвер як відвідуваний і відзначаємо Даллас як поточний.

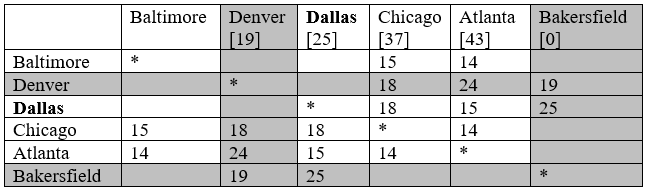
$clipboard_e712dc3c5e7835dfab45640e51dea54f0.png$

Крок 2 (#3): Для міст, підключених до Далласа, обчисліть відстань до кінця. Для Чикаго відстань від Чикаго до Далласа становить 18, а від Далласа до кінця - 25, тому відстань від Чикаго до кінця через Даллас складе 18+25 = 43. Оскільки це більше, ніж позначена в даний час відстань для Чикаго, ми не замінюємо його. Для Атланти обчислюємо 15+25 = 40. Оскільки це коротше, ніж позначена в даний час відстань для Атланти, ми замінюємо існуючу відстань.

Крок 3 і 4 (#3): Ми відзначаємо Даллас як відвідуваний і відзначаємо Чикаго як поточний.

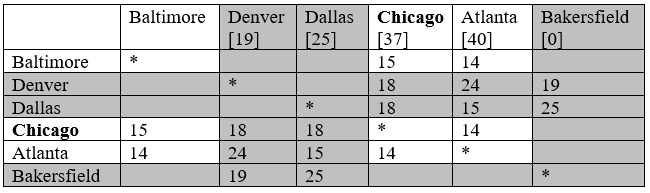
$clipboard_ebf2973d1d12fecdccbec6fd90a959810.png$

Крок 2 (#4): Балтімор і Атланта - єдині невідвідувані міста, пов'язані з Чикаго. Для Балтімора ми обчислюємо 15+37 = 52 і відзначаємо цю відстань. Для Атланти обчислюємо 14+37 = 51. Оскільки це більше, ніж існуюча відстань 40 для Атланти, ми не замінюємо цю відстань.

Крок 3 і 4 (#4): Позначте Чикаго як відвідуваний, а Атланту як поточну.

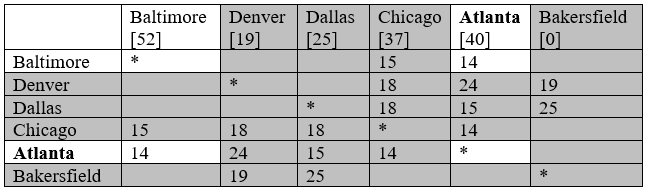
$clipboard_e51f52531779084f400b21d9aeade2271.png$

Крок 2 (#5): Відстань від Атланти до Балтімора становить 14. Додамо, що до вже розрахованої відстані для Атланти дається загальна відстань 14+40 = 54 години від Балтімора до Бейкерсфілда через Атланту. Оскільки це більше, ніж розрахована на даний момент відстань, ми не замінюємо відстань для Балтімора.

Крок 3 і 4 (#5): Ми відзначаємо Атланту як відвідувану. Всі міста відвідали, і ми закінчили.

Найкоротший маршрут з Балтімора до Бейкерсфілда займе 52 години, і пройде через Чикаго і Денвер.

Спробуйте зараз 2

Знайдіть найкоротший шлях між вершинами A та G на графіку нижче.

$gt19.svg$

Відповідь: Найкоротший шлях - ABDEG, довжиною 13

[1] Це може бути зроблено для швидшого запуску через різні оптимізації до реалізації.