6.8: Вправа

Last updated
Save as PDF

Page ID: 66222

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Навички

1. Щоб доставити пошту в конкретному районі, поштовому перевізнику необхідно пройтися по кожній з вулиць з будинками (крапками). Створіть графік з краями, що показує, де перевізник повинен ходити, щоб доставити пошту.

$gt61.svg$

2. Припустимо, що місто має 7 мостів, як показано нижче. Створіть графік, за допомогою якого можна визначити, чи є шлях, який перетинає всі мости один раз.

$gt62.svg$

3. У таблиці нижче наведено приблизний час їзди (у хвилинах, без руху) між п'ятьма містами в районі Далласа. Створіть зважений графік, що представляє ці дані.

\ (\ begin {масив} {|l|l|l|l|l|}
\ hline &\ text {Плано} &\ текст {Мескіт} &\ текст {Арлінгтон} &
\ текст {Дентон}\\ hline\ текст {Форт-Ворт} & 54 & 52 & 19\\\ hline\ текст {Плано} & 38 & 53\\

\ hline\ текст {Мескіт} & & 43 & 56\
\ hline\ text {Арлінгтон} & & 50\
\ hline
\ end {масив}\)

4. У таблиці нижче наведені авіаквитки в один бік між 5 містами [1]. Створіть графік, що відображає ці дані.

\ (\ begin {масив} {|l|l|l|l|l|}
\ hline &\ текст {Гонолулу} &\ текст {Лондон} &\ текст {Москва} &\ текст {Каїр}\
\ hline\ текст {Сіетл} &\ $159 &\ $370 &\ $654 &\ $684\\
\ hline\ текст {Гонолулу} &\ $830 &\ $854 &\ $801\\
\ hline\ текст {Лондон} & &\ $245 &\ $323\\
\ hline\ text {Москва} & &\\ $329\
\ hline
\ кінець {масив}\)

5. Знайдіть ступінь кожної вершини на графіку нижче.

$gt63.svg$

6. Знайдіть ступінь кожної вершини на графіку нижче.

$gt64.svg$

7. Які з цих графіків пов'язані?

$gt65.svg$

8. Які з цих графіків пов'язані?

$gt66.svg$

9. Час проїзду залізницею для сегмента системи Eurail наведено нижче з часом у дорозі в годині та хвилинах [2]. Знайдіть шлях з найкоротшим часом у дорозі з Берна до Берна, застосувавши алгоритм Дейкстри.

$gt67.svg$

10. Використовуючи графік з попередньої задачі, знайдіть шлях з найкоротшим часом шляху від Парижа до Мюнхена.

11. Чи кожен з цих графіків має схему Ейлера? Якщо так, знайдіть його.

$gt68.svg$

12. Чи кожен з цих графіків має схему Ейлера? Якщо так, знайдіть його.

$gt69.svg$

13. Еулерізуйте цей графік, використовуючи якомога менше дублікатів країв. Потім знайдіть схему Ейлера.

$gt70.svg$

14. Еулерізуйте цей графік, використовуючи якомога менше дублікатів країв. Потім знайдіть схему Ейлера.

$gt71.svg$

15. Обслуговуючий персонал в парку розваг повинен патрулювати основні доріжки, показані на графіку нижче, збираючи сміття. Знайдіть ефективний маршрут патрулювання, знайшовши схему Ейлера. При необхідності ефективно еулерізуйте графік.

$gt72.svg$

16. Після шторму міський екіпаж оглядає на наявність дерев або щітки, що перекривають дорогу. Знайдіть ефективний маршрут для околиць нижче, знайшовши схему Ейлера. При необхідності ефективно еулерізуйте графік.

$gt73.svg$

17. Чи кожен з цих графіків має принаймні одну гамільтонівську схему? Якщо так, знайдіть його.

$gt74.svg$

18. Чи кожен з цих графіків має принаймні одну гамільтонівську схему? Якщо так, знайдіть його.

$gt75.svg$

19. Компанія повинна доставити продукт до кожного зі своїх 5 магазинів навколо Далласа, штат Техас. Відстані їзди між магазинами наведені нижче. Знайдіть маршрут для водія, який слід дотримуватися, повертаючись до розподільного центру у Форт-Уерті:

Використання найближчого сусіда, починаючи з Форт-Уерта
Використання повторюваного найближчого сусіда
Використання відсортованих країв

20. Продавець повинен подорожувати з Сіетла до Гонолулу, Лондона, Москви та Каїра. Скористайтеся таблицею витрат на переліт з проблеми #4, щоб знайти маршрут для цієї людини, щоб слідувати:

Використання найближчого сусіда, починаючи з Сіетла
Використання повторюваного найближчого сусіда
Використання відсортованих країв

21. При установці волоконної оптики деякі компанії встановлять кільце сонет; повний шлейф кабелю, що з'єднує кілька місць. Це використовується для того, щоб при пошкодженні будь-якої частини кабелю він не переривав обслуговування, так як є друге підключення до хаба. Компанія має 5 корпусів. Витрати (в тисячах доларів) на прокладку кабелів між парами будівель наведені нижче. Знайдіть схему, яка дозволить мінімізувати витрати:

Використання найближчого сусіда, починаючи з будівлі A
Використання повторюваного найближчого сусіда
Використання відсортованих країв

$gt76.svg$

22. Турист хоче відвідати 7 міст Ізраїлю. Відстані водіння, у кілометрах, між містами наведені нижче [3]. Знайдіть маршрут, за яким людина буде слідувати, повертаючись до стартового міста:

Використання найближчого сусіда, починаючи з Єрусалиму
Використання повторюваного найближчого сусіда
Використання відсортованих країв

\ (\ begin {масив} {|l|l|l|l|l|l|l|}
\ hline &\ text {Єрусалим} &\ текст {Тель-Авів} &\ текст {Хайфа} &\ text {Беер-Шева} &\
текст {Ейлат}\\ hline\ текст {Єрусалим} &\\ hline
\ text { Тель-Авів} & 58 &\ _ &\\\ hline
\ текст {Хайфа} & 151 & 95 &\ _ &\\\ hline
\ текст {Тверія} & 152 & 134 & 69 &\\\\ hline
\ текст {Беер-Шева} & 81 & 105 & 197 & 233 &\\ _ &\
\ hline\ текст {Ейлат} & 309 & 346 & 438 & 405 & 241 &\ _\\
\ hline\ текст {Назарет} & 131 & 102 & 35 & 29 & 207 & 488\
\ hline
\ кінець {масив}\)

23. Знайдіть мінімальну вартість охоплюючого дерева для графіка, який ви створили в задачі #3

24. Знайдіть мінімальну вартість охоплюючого дерева для графіка, який ви створили в задачі #22

25. Знайти мінімальну вартість охоплюючого дерева для графіка з задачі #21

Поняття

26. Чи може граф мати одну вершину з непарним ступенем? Якщо ні, чи є інші значення, які неможливі? Чому?

27. Повний графік - це той, в якому є ребро, що з'єднує кожну вершину з будь-якою іншою вершиною. Для яких значень n повний граф з n вершинами має схема Ейлера? Гамільтонова траса?

28. Створіть графік, намалювавши n вершин у рядку, потім ще n вершин нижче цих. Намалюйте ребро від кожної вершини у верхньому ряду до кожної вершини нижнього ряду. Приклад, коли n = 3 наведено нижче. Для яких значень n граф, створений таким чином, матиме схему Ейлера? Гамільтонова траса?

$gt77.svg$

29. Еулерізуйте цей графік найбільш ефективним способом, враховуючи вагу ребер.

$gt78.svg$

30. Еулерізуйте цей графік найбільш ефективним способом, враховуючи вагу ребер.

$gt79.svg$

31. Еулерізуйте цей графік найбільш ефективним способом, враховуючи вагу ребер.

$gt80.svg$

32. Еулерізуйте цей графік найбільш ефективним способом, враховуючи вагу ребер.

$gt81.svg$

Розвідки

33. Соціальні мережі, такі як Facebook та LinkedIn, можуть бути представлені за допомогою графіків, в яких вершини представляють людей, а ребра малюються між двома вершинами, коли ці люди є «друзями». У таблиці нижче наведена таблиця дружби, де X показує, що двоє людей є друзями.

34.

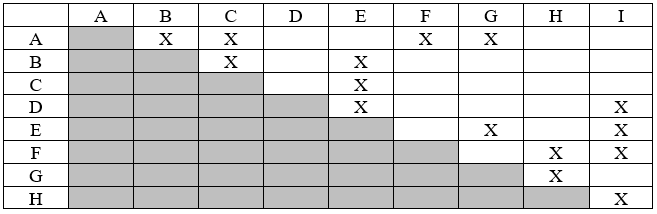
$clipboard_e9d8d6a5999cfca4a827ae51c9a3ab95b.png$

Створіть графік цієї таблиці дружби
Знайти найкоротший шлях від А до Д. Довжина цього шляху часто називають «ступенями розлуки» двох людей.
Розширення: Розділити на групи. Кожна група забере 10 або більше фільмів, і шукати своїх головних акторів (www.imdb.com є хорошим джерелом). Створіть графік з кожним актором як вершину, а ребра з'єднують двох акторів у одному фільмі (зверніть увагу на назву фільму на краю). Знайдіть цікаві шляхи між акторами та вікторини інших груп, щоб побачити, чи можуть вони вгадати зв'язки.

35. Перевірка орфографії в програмі обробки текстів робить пропозиції, коли він знаходить слово не в словнику. Щоб визначити, які слова підказати, намагається знайти схожі слова. Однією мірою схожості слів є відстань Левенштейна, яка вимірює кількість замін, доповнень або вилучень, необхідних для зміни одного слова на інше. Наприклад, слова spis і spot - це відстань 1 один від одного; зміна коси на пляму вимагає однієї заміни (i для o). Аналогічно, коса - це відстань 1 від ями, оскільки зміна вимагає одного видалення (і). Слово зло також відстань 1 від коси, оскільки воно вимагає одного додавання (е). Слово сажа - це відстань 2 від коси, оскільки потрібні дві заміни.

Створіть графік, використовуючи слова як вершини та ребра, що з'єднують слова з відстанню Левенштейна 1. Використовуйте неправильно написане слово «moke» як центр, і спробуйте знайти принаймні 10 пов'язаних словникових слів. Як перевірка орфографії може використовувати цей графік?
Покращуйте метод зверху, призначивши вагу кожному ребру на основі ймовірності підміни, додавання або видалення. Ви можете базувати ваги на будь-якому розумному підході: близькість клавіш на клавіатурі, загальні мовні помилки тощо Використовуйте алгоритм Дейкстри, щоб знайти довжину найкоротшого шляху від кожного слова до «moke». Як перевірка орфографії може використовувати ці значення?

36. Графік нижче містить дві вершини непарного ступеня. Для евлерізації цього графа необхідно продублювати ребра, що з'єднують ці дві вершини.

Використовуйте алгоритм Дейкстри, щоб знайти найкоротший шлях між двома вершинами з непарним ступенем. Це виробляє найбільш ефективну евлерізацію та вирішує проблему китайського листоноші для цього графіка?

$gt82.svg$

Припустимо, граф має$n$ непарні вершини. Використовуючи підхід з частини а, скільки найкоротших шляхів потрібно було б розглянути? Чи буде такий підхід ефективним?

[1] Найдешевші тарифи, знайдені при отриманні 1 вересня 2009 року для подорожей 22 вересня 2009

[2] З www.eurail.com/eurail-залізнична карта

[3] З http://www.ddtravel-acc.com/Israel-c...s-distance.htm