Skip to main content
LibreTexts - Ukrayinska

6.2: Графіки

  1. Last updated
  2. Save as PDF
  • Page ID
    66245

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Креслення графіків

    Приклад 1

    Ось частина житлового комплексу з Міссули, штат Монтана [1]. В рамках своєї роботи інспектор газону розвитку повинен йти по кожній вулиці в розвитку, переконавшись, що озеленення домовласників відповідає вимогам громади.

    clipboard_e3234824b359f527fc7293e4adc684a2c.png

    Рішення

    Природно, вона хоче мінімізувати кількість прогулянок, яку їй доводиться робити. Чи можливо їй ходити по кожній вулиці в цьому розвитку без необхідності робити будь-які зворотні відступи? Хоча ви можете відповісти на це питання, просто подивившись на картину на деякий час, було б ідеально мати можливість відповісти на питання для будь-якої картини незалежно від її складності.

    Для цього нам спочатку потрібно спростити картинку в форму, з якою легше працювати. Ми можемо зробити це, намалювавши просту лінію для кожної вулиці. Там, де перетинаються вулиці, розміщуємо крапку.

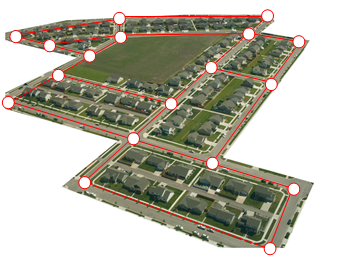
    clipboard_efd3110477b5288027be3334e3b6f4634.pnggt2.svg

    Цей тип спрощеної картинки називається графом.

    Графіки, вершини та ребра

    Граф складається з набору точок, званих вершинами, і набору ребер, що з'єднують пари вершин.

    Поки ми малювали наш оригінальний графік, щоб відповідати малюнку, який ми мали, немає нічого особливо важливого в макеті, коли ми аналізуємо графік. Обидва наведені нижче графіки еквівалентні намальованому вище, оскільки вони показують ті самі крайові зв'язки між тими ж вершинами, що і вихідний графік.

    gt3.svg

    Ви, напевно, вже помітили, що ми використовуємо термін графік інакше, ніж ви, можливо, використовували термін в минулому для опису графіка математичної функції.

    Приклад 2

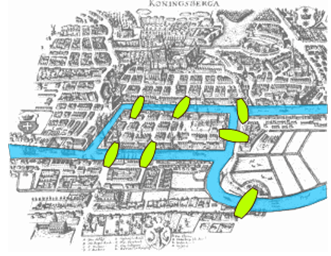    clipboard_e28b234701a5f1bdb02e13cff366ed8e3.pngЩе в 18 столітті в прусському місті Кенігсберг через місто протікала річка і сім мостів перетнули розвилки річки. Річка і мости виділені на малюнку праворуч [2].

    Як розваги вихідних, обивателі побачать, чи зможуть вони знайти маршрут, який би провів їх через кожен міст один раз і повернув їх туди, де вони почали.

    Рішення

    Леонард Ейлер (вимовляється Oy-lur), один з найбільш плідних математиків коли-небудь, розглянув цю проблему в 1735 році, заклавши основу теорії графів як поля в математиці. Щоб проаналізувати цю задачу, Ейлер ввів ребра, що представляють мости:

    gt4.svg

    Оскільки розмір кожної сухопутної маси не має відношення до питання мостових переходів, кожен може бути скорочений до вершини, що представляє місце розташування:

    gt5.svg

    Зверніть увагу, що на цьому графіку є два ребра, що з'єднують північний берег і острів, що відповідають двом мостам на оригінальному кресленні. Залежно від інтерпретації ребер і вершин, відповідних сценарію, цілком можливо і розумно мати більше одного ребра, що з'єднує дві вершини.

    Хоча ми ще не відповіли на фактичне питання про те, чи існує маршрут, який перетинає кожен міст один раз і повертається до початкового місця, графік забезпечує основу для вивчення цього питання.

    Визначення

    Хоча раніше ми вільно визначили деяку термінологію, ми зараз спробуємо бути більш конкретними.

    Вершина

    Вершина - це точка на графіку, яка може представляти перетин вулиць, земельну масу або загальне розташування, наприклад «робота» або «школа». Вершини часто з'єднуються ребрами. Зауважте, що вершини виникають лише тоді, коли точка явно розміщена, а не коли два ребра перетинаються. Уявіть собі шляхопровід автостради - перетин автостради та бічної вулиці, але переїхати з бічної вулиці на автостраду в цій точці неможливо, тому немає перетину і не буде розміщена вершина.

    Краї

    Ребра з'єднують парами вершин. Край може представляти фізичний зв'язок між місцезнаходженнями, як вулиця, або просто те, що існує маршрут, що з'єднує два місця, як рейс авіакомпанії.

    Петля

    Петля - це особливий тип ребра, який з'єднує вершину з собою. Петлі не використовуються багато в графіках вуличної мережі.

    gt6.svg

    Ступінь вершини

    Ступінь вершини - це кількість ребер, що зустрічаються на цій вершині. Можливо, щоб вершина мала ступінь нулю або більше.

    gt7.svg

    Шляхи

    Шляхом є послідовність вершин з використанням ребер. Зазвичай нас цікавить шлях між двома вершинами. Наприклад, шлях від вершини A до вершини M показаний нижче. Це один з багатьох можливих шляхів у цьому графіку.

    gt8.svg

    Ланцюг

    Схема - це шлях, який починається і закінчується в одній вершині. Схема, що починається і закінчується на вершині А, показана нижче.

    gt9.svg

    Підключений

    Граф з'єднується, якщо є шлях від будь-якої вершини до будь-якої іншої вершини. Кожен графік, намальований досі, був пов'язаний. Графік нижче від'єднаний; немає можливості дістатися від вершин зліва до вершин праворуч.

    gt10.svg

    Ваги

    Залежно від проблеми, що вирішується, іноді по краях призначаються ваги. Ваги можуть відображати відстань між двома місцями, час у дорозі або вартість поїздки. Важливо зазначити, що відстань між вершинами в графі не обов'язково відповідає вазі ребра.

    Спробуйте зараз 1

    На графіку нижче показано 5 міст. Ваги по краях відображають авіаквиток для польоту в один бік між містами.

    1. Скільки вершин і ребер має граф?
    2. Чи пов'язаний графік?
    3. Яка ступінь вершини, що представляє ЛА?
    4. Якщо ви летите з Сіетла в Даллас до Атланти, це шлях або схема?
    5. Якщо ви летите з Лос-Анджелеса в Чикаго до Далласа до Лос-Анджелеса, це шлях чи схема?

    gt11.svg

    Відповідь

    a. 5 вершин, 10 ребер

    б. так, він підключений

    c Вершина - ступінь 4

    d. шлях

    е. схема

    [1] Сем Бібі. http://www.flickr.com/photos/sbeebe/2850476641/, КС-BY

    [2] Богдан Джушка. http://en.Wikipedia.org/wiki/File:Ko...rg_bridges.png