14.2: Розрахунок прибутковості облігації
- Page ID
- 66723
Чи повинні ви завжди тримати облігацію до погашення? Чи є найкращий час для продажу? Відкриваючи останній розділ, ви інвестували в 10 Уряд Канади $5,000 номінальної вартості облігацій з 5% купоном і 20 років, що залишилися до погашення. За них ви заплатили $4,699,02 кожен, коли переважаючі ставки облігацій становили 5,5%. Через десять років після того, як ви придбали ці облігації, переважаючі ринкові ставки облігацій знизилися до 3.35%, але, як очікується, зростуть найближчим часом. Зараз настав час продати ці облігації?
Це складне рішення з багатьма змінними; однак, щоб допомогти прийняти це рішення, ви повинні знати принаймні три критичні частини інформації: ціну продажу облігації, прибутковість, яку ви зрозуміли б від своїх інвестицій, якщо ви тримаєте облігацію до погашення, і прибутковість, якщо ви продали облігацію. сьогодні.
Цей розділ об'єднує розрахунки цін на облігації та прибутковості облігацій, щоб ви краще розуміли свої інвестиції в облігації. Ці вказівки застосовуються незалежно від того, чи інвестуєте ви особисто або від імені вашої компанії.
Прибутковість до погашення
Прибутковість до погашення, також відома як основа, - це загальна норма прибутку облігацій при придбанні за ринковою ціною і утримується до погашення. Він включає як піврічні відсотки, які власники облігацій заробляють на своїх інвестиціях, а також прибуток або збиток, що виникають внаслідок різниці між ринковою ціною на дату продажу та ціною викупу. Ця прибутковість до погашення в точності дорівнює ринковій нормі прибутку на дату покупки. Таким чином, у наведеному вище прикладі, якщо ви тримаєтесь за ці облігації до погашення, ви зрозумієте прибутковість до погашення 5,5%.
У цьому розділі ви обертаєтеся від розрахунків з розділу 14.1, де ви відповіли на питання: «Знаючи ринкову норму прибутку, що ви будете платити?» Тепер вас запитують: «Знаючи, що ви платите, яка ринкова норма прибутку?» Таким чином, переформулювання вступного прикладу ви мали б: «Якби ви заплатили $4,699,02 за облігацію номінальної вартості $5,000 з 20 років до погашення, маючи 5% купон, яку прибутковість до погашення ви б зрозуміли?»
Формула
Y вам не потрібні нові формули для розрахунку прибутковості облігації до погашення. Мета полягає в тому, щоб вирішити за номінальну процентну ставку, або\(IY\). Ви повинні працювати з формулами 14.2, 14.3 та 9.1. Нагадаємо, що за формулою 14.2 визначається піврічна сума виплати купонного відсотка за облігаціями. Ви підставляєте цю суму у формулу 14.3, яка обчислює ціну облігації на дату виплати відсотків. Однак у цьому випадку ви повинні вирішити Формулу 14.3 не для ціни дати, а для періодичної процентної ставки, або я Як тільки ви знаєте періодичну процентну ставку, ви можете замінити її в Формулу 9.1 і вирішити для номінальної процентної ставки, або\(IY\).
Однією з проблем використання формульного підходу є те, що неможливо алгебраїчно виділити періодичну процентну ставку i n Формула 14.3 . Ви повинні звернутися до таких технологій, як калькулятор BAII Plus або Excel.
Як це працює
Виконайте наступні дії, щоб розрахувати прибутковість облігації до погашення:
Крок 1: Намалюйте часову шкалу, подібну до представленої тут, починаючи від дати продажу до дати погашення. Визначте всі відомі змінні.

Крок 2: Використовуючи формулу 14.2 , розрахуйте суму виплати відсотків за облігаціями.
Крок 3: Як і в розділі 14.1, використовуйте формулу 11.1 для обчислення\(N\). Оскільки ринкова ставка та купонна ставка є як піврічними,\(N\) то використовується як загальна кількість з'єднань, так і загальна кількість платежів.
- Якщо використовується ручний метод, підставити всі відомі числа в Формулу 14.3 і спробувати вирішити періодичну процентну ставку (\(i\)). Як тільки ви це дізнаєтеся, перетворіть його на номінальну процентну ставку за допомогою Формули 9.1.
- Крім того, якщо ви використовуєте таку технологію, як калькулятор, введіть всі відомі змінні та вирішуйте безпосередньо для номінальної процентної ставки (\(IY\)).
Важливі зауваження
Зверніть увагу на дві умови, коли ви розраховуєте прибутковість до погашення:
- Торгівля відбувається тільки в дати виплати відсотків.
- Власник облігацій реінвестує всі купонні виплати за однаковою ставкою відсотків. Розрахунки, які не відповідають цим умовам, виходять за рамки вступної сфери цього підручника.
Якщо ви купуєте облігацію з купонною ставкою 4%, коли ринкова ставка 5%, яку прибутковість до погашення ви зрозумієте?
- Відповідь
-
5%; ваша прибутковість до погашення залежить від ринкової ставки, а не від ставки купона.
Припустимо, облігація номінальної вартості $10,000 купується за $7,688.52 з 20 років до погашення і має купонну ставку 4% піврічних. Яку прибутковість усвідомить власник облігацій, якщо вона тримає її до погашення?
Рішення
Прибутковість до погашення являє собою номінальну процентну ставку по облігації, або\(IY\).
Що ви вже знаєте
Крок 1:
Графік продажу облігацій відображається нижче.
Виплата купонного\(CPN\) відсотка: = 4%,\(CY\) = 2, номінал = $10,000
Облігація: Ціна дати = 7 688,52 доларів,\(FV\) = 10 000 доларів,\(CY\) = 2,\(PMT_{BOND}\) = Формула 14.2,\(PY\) = 2, роки залишилися = 20
Як ви туди потрапите
Крок 2:
Застосовуйте формулу 14.2 для визначення періодичної виплати відсотків за облігаціями.
Крок 3:
Застосовуйте формули 11.1, 14.3 та 9.1 для визначення прибутковості до погашення (\(IY\)). Вирішіть формули 14.3 і 9.1 за допомогою калькулятора.

Розрахунки
Крок 2:
\[PMT_{BOND}=\$ 10,000 \times \dfrac{0.04}{2}=\$ 200 \nonumber \]
Крок 3:
\(N=2 \times 20=40\)(сполуки та платежі)
\[\$ 7,688.52=\dfrac{\$ 10,000}{(1+i)^{40}}+\$ 200\left[\dfrac{1-\left[\dfrac{1}{1+i}\right]^{40}}{i}\right] \quad i=\dfrac{\mathrm{IY}}{2} \nonumber \]
Вихід калькулятора\(= IY = 6%\)
Інструкції з калькулятора
| Режим | П | В/У | ПВ |
|---|---|---|---|
| КІНЕЦЬ | 40 | Відповідь: 6.000002 | -7688.52 |
| PMT | ФВ | П/У | С/У |
|---|---|---|---|
| 200 | 10 000 | 2 | 2 |
Якщо вона тримається на облігації протягом наступних 20 років, вона реалізує прибутковість до погашення 6%, що складається піврічно.
Прибутковість інвестора
Розрахунок прибутковості до погашення вимагає, щоб облігація тримала до дати її погашення, після чого відома майбутня ціна викупу вартості та дорівнює її номіналу. Однак ця умова може і не триматися. Власник облігацій може продати облігацію в будь-який момент до дати погашення. Якщо облігація продається, майбутня вартість базується на переважній ставці облігацій на той час, і ціна, як правило, не дорівнює її номіналу. Яка ж тоді прибутковість облігацій для інвестора?
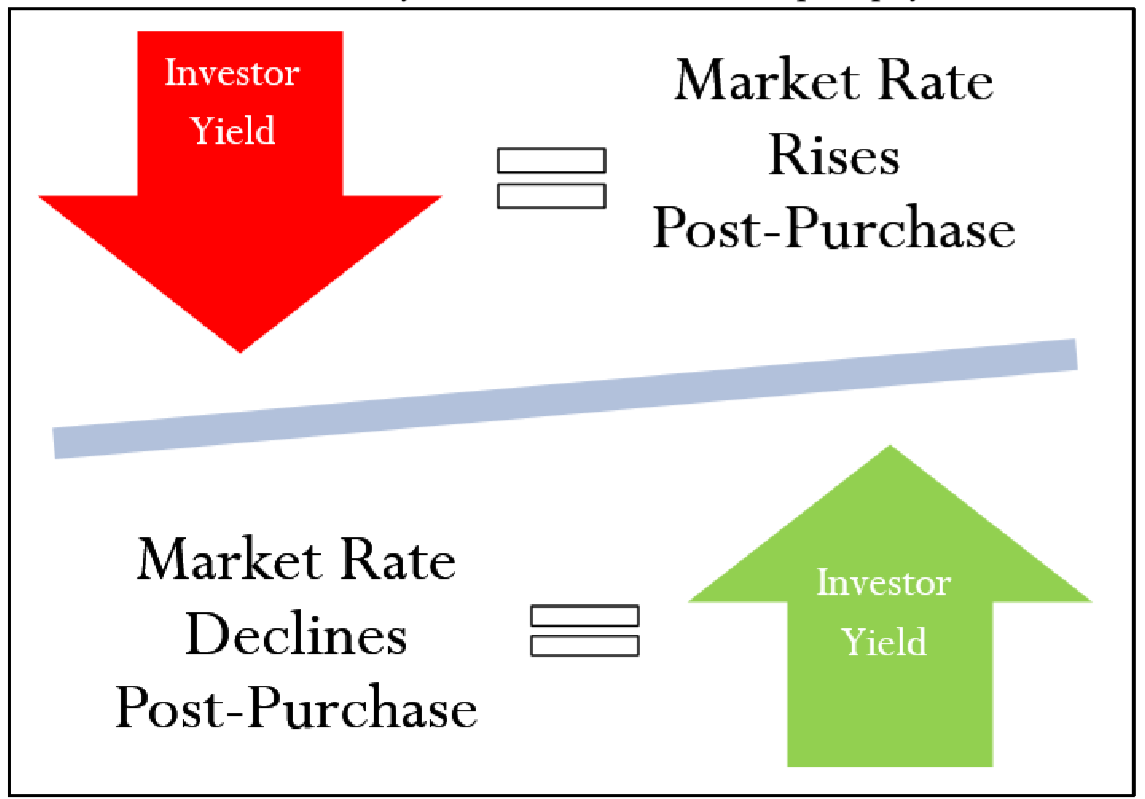
Малюнок\(\PageIndex{1}\): Дохідність інвестора
Дохідність інвестора складається з купонних виплат, які були отримані, поки інвестор володіє облігацією разом з різницею, досягнутою між ціною покупки та ціною продажу. Наведена вище цифра ілюструє, що відбувається з прибутковістю інвестора, пов'язуючи ринкову ставку після покупки та прибутковість інвестора.
- Коли ринкова ставка зростає після придбання облігації, інвестор відчуває нижчу прибутковість, ніж початкова прибутковість до погашення, оскільки майбутня ціна продажу облігацій знижується. Припустимо, що інвестори купують облігацію за ринковою ставкою 5%:
- Якщо вони утримують його до погашення, вони досягають 5% прибутковості до погашення.
- Якщо замість цього вони продають облігацію до погашення, коли ринкова ставка становить 6%, прибутковість інвестора становить менше 5%.
- Коли ринкова ставка знижується після придбання облігації, інвестор відчуває більш високу прибутковість, ніж початкова прибутковість до погашення, оскільки майбутня ціна продажу облігацій збільшується. Припустимо ще раз, що інвестори купують облігацію за ринковою ставкою 5%:
- Якщо вони тримають його до погашення, вони, звичайно, досягають 5% прибутковості до погашення.
- Якщо вони продають облігацію, коли ринкова ставка становить 4%, прибутковість інвестора становить більше 5%.
Формула
Існуючих формул облігацій достатньо для розрахунку прибутковості інвестора. Для визначення суми виплати купона облігацій вам потрібна формула 14.2. Ви використовуєте Formula 14.3 для розрахунку як ціни покупки, так і ціни продажу. Потім ви використовуєте його втретє для вирішення періодичної процентної ставки. Коли ви вирішуєте\(i\), майбутня вартість облігації, яку ви підставляєте у формулу, повинна бути ціною продажу облігації на майбутню дату, а не ціною викупу.
Як це працює
Виконайте наступні дії, щоб розрахувати прибутковість інвестора:
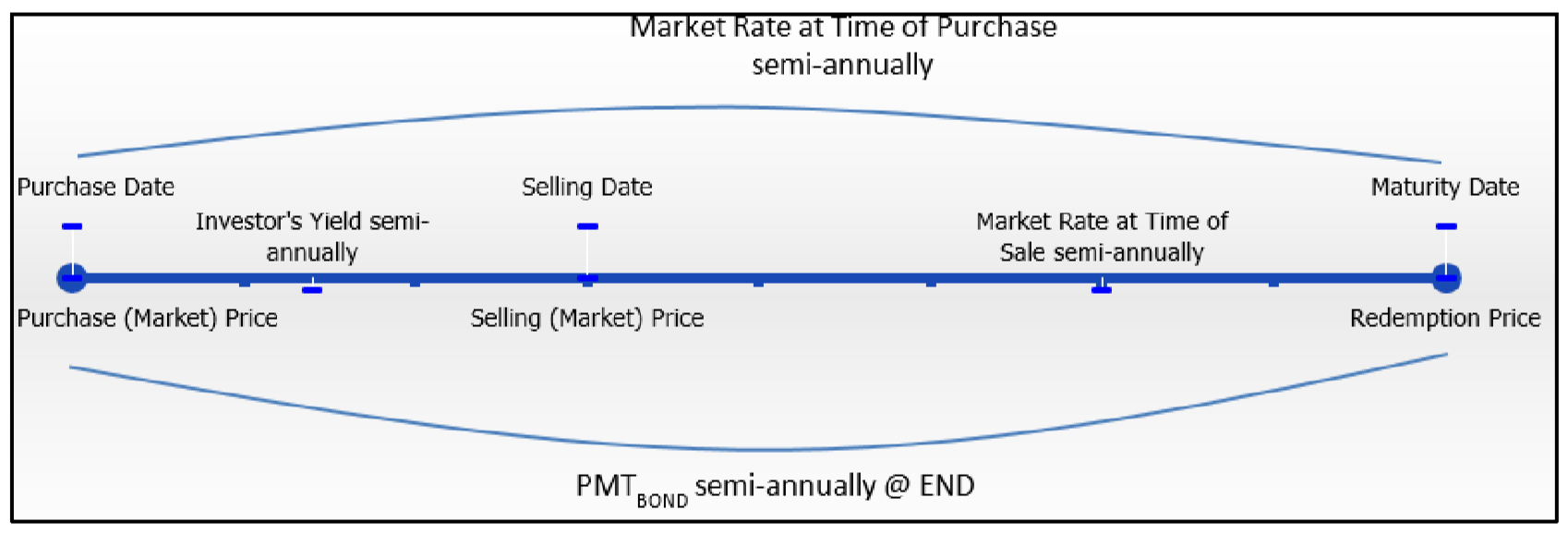
Крок 1: Намалюйте часову шкалу, подібну до зображеної тут, починаючи від дати покупки до дати погашення. Чітко вказуємо дату продажу. Визначте всі відомі змінні.
Крок 2: Використовуючи формулу 14.2, розрахуйте суму виплати відсотків за облігаціями.
Крок 3: Якщо потрібно, розрахуйте ціну покупки за допомогою Формули 14.3. Як і в попередніх процедурах, використовуйте Формулу 11.1 для розрахунку піврічних на основі,\(N\) що представляє як загальну кількість з'єднань, так і загальну кількість платежів. Використовуйте ринкову ставку на момент покупки.
Крок 4: Якщо потрібно, розрахуйте ціну продажу за допомогою Формули 14.3 таким же чином. Використовуйте ринкову ставку на момент продажу.
Крок 5: Вирішіть номінальну процентну ставку (\(IY\)) між датою покупки та датою продажу. Ціна покупки - це ціна дати, а ціна продажу - майбутня вартість (\(FV\)).
- Якщо використовується ручний метод, підставити всі відомі числа в Формулу 14.3 і вирішити для періодичної процентної ставки (\(i\)). Перетворіть його в номінальну процентну ставку за допомогою Формули 9.1.
- Як варіант, якщо за допомогою такої технології, як калькулятор, то введіть всі відомі змінні і вирішуйте безпосередньо для номінальної процентної ставки (IY).
Важливі зауваження
Ті самі дві вимоги, що застосовуються до розрахунку прибутковості до погашення, зберігаються при розрахунку прибутковості інвестора:
- Торгівля відбувається тільки в дати виплати відсотків.
- Власник облігацій реінвестує всі купонні виплати за однаковою ставкою відсотків.
У кожному з наступних визначте, чи збільшується прибутковість інвестора, зменшується або залишається колишньою.
- Облігація купується, коли ринкова прибутковість становить 5%, а потім продається, коли ринкова ставка становить 5%.
- Облігація купується, коли ринкова прибутковість становить 5%, а потім продається, коли ринкова ставка становить 6%.
- Відповідь
-
- Збільшується; нижча ринкова ставка призводить до зростання ціни продажу.
- Те саме; жодна зміна ринкової ставки не призводить до зміни прибутковості.
- Зменшується; більш високий ринковий курс призводить до зниження ціни продажу
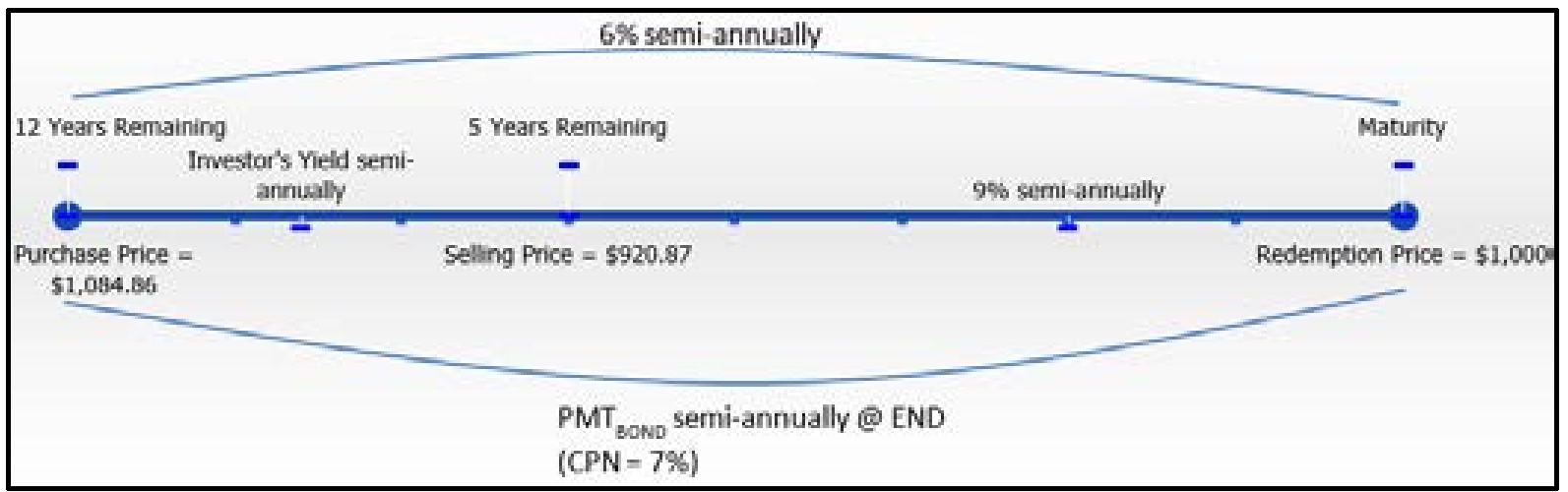
Облігація номінальної вартості $1,000 з купоном 7% і 12 років до погашення була придбана за $1,084,68, коли ринкові ставки становили 6%. Він продавався через сім років за 920,87 доларів, коли ринкові ставки становили 9%. Яку прибутковість усвідомив власник облігацій?
Рішення
Дохідність інвестора являє собою номінальну процентну ставку по облігації протягом часу, коли інвестор володів облігацією, або\(IY\).
Що ви вже знаєте
Крок 1:
Терміни купівлі-продажу облігації відображаються нижче.
Виплата купонного\(CPN\) відсотка: = 7%,\(CY\) = 2, номінал = $1,000 Купівля/продаж
Облігація:\(PV\) = $1,084,68,\(FV\) = $920,87,\(CY\) = 2,\(PMT_{BOND}\) = Формула 14.2,\(PY\) = 2, Проведені роки = 7
Як ви туди потрапите
Крок 2:
Застосовуйте формулу 14.2 для визначення періодичної виплати відсотків за облігаціями.
Крок 3:
Визначте ціну покупки облігацій. Він відомий на рівні $1,084,68 і його не потрібно розраховувати. Це дата ціна для кроку 5.
Крок 4:
Визначте ціну продажу облігацій. Він відомий в $920.87 і його не потрібно розраховувати. Це майбутнє значення (\(FV\)) для кроку 5.
Крок 5:
Застосовуйте формули 11.1, 14.3 та 9.1 для визначення прибутковості інвестора (\(IY\)). Вирішіть формули 14.3 і 9.1 за допомогою калькулятора.
Виконувати
Крок 2:
\[PMT_{BOND}=\$ 1,000 \times \dfrac{0.07}{2}=\$ 35 \nonumber \]
Крок 5:
\(N=2 \times 7=14\)(сполуки та платежі)
\[\$ 1,084.68=\dfrac{\$ 920.87}{(1+i)^{14}}+\$ 35\left[\dfrac{1-\left[\dfrac{1}{1+i}\right]^{14}}{i}\right] \quad i=\dfrac{I Y}{2} \nonumber \]
Вихід калькулятора\(= IY=4.6003 \%\)
Інструкції з калькулятора
| Режим | П | В/У | ПВ |
|---|---|---|---|
| КІНЕЦЬ | 14 | Відповідь: 4.600320 | -1084.68 |
| PMT | ФВ | П/У | С/У |
|---|---|---|---|
| 35 | 920.87 | 2 | 2 |
Ринкова ціна облігацій значно знизилася через зростання ринкової ставки на 3% протягом семирічного періоду часу. Таким чином, інвестор не реалізує початкову прибутковість до погашення 6% (ринкова ставка), а фактично прибутковість інвестора знизилася до 4,6003%, що посилюється піврічно.
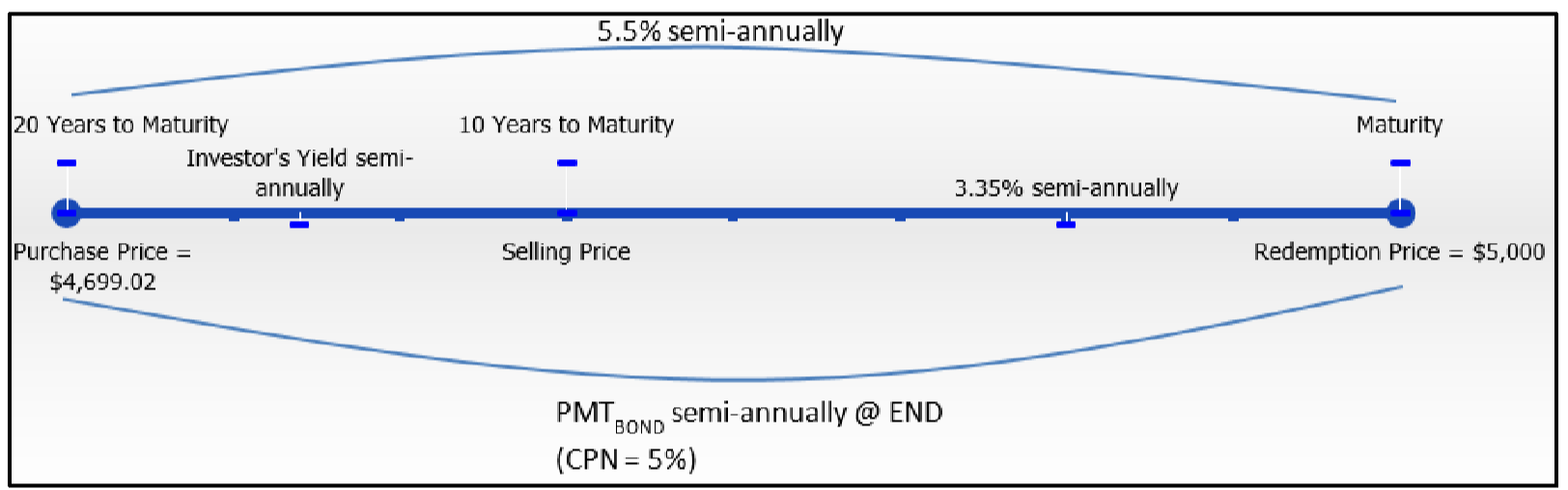
Під час вступних дискусій до розділів 14.1 та 14.2 ви інвестували в 10 Уряд Канади облігації номінальної вартості в розмірі 5000 доларів США з купоном 5% та 20 роками, що залишилися до погашення, заплативши $4,699,02 кожен, коли переважаючі ставки облігацій становили 5,5%. Ви помітили сьогодні, через 10 років, що переважаючі ставки облігацій знизилися до 3,35%. Яку прибутковість інвестора ви зрозуміли б, якби продали свої облігації сьогодні?
Рішення
Вам потрібно розрахувати прибутковість лише для однієї з 10 облігацій, оскільки, звичайно, прибутковість однакова для всіх облігацій. Дохідність інвестора являє собою номінальну процентну ставку по облігації протягом часу, коли ви володієте облігацією, або\(IY\).
Що ви вже знаєте
Крок 1:
Терміни купівлі-продажу облігації відображаються нижче.
Виплата купонного\(CPN\) відсотка: = 5%,\(CY\) = 2, номінал = $5,000
Придбання облігацій:\(PV\) = $4,699.02
Продаж облігацій:\(FV\) = $5,000,\(IY\) = 3.35%,\(CY\) = 2,\(PMT_{BOND}\) = Формула 14.2,\(PY\) = 2, роки залишилися = 10
Купівля/продаж облігацій:\(PV\) = $4,699,02,\(FV\) = Ціна продажу,\(CY\) = 2,\(PMT_{BOND}\) = Формула 14.2,\(PY\) = 2, Проведені роки = 10
Як ви туди потрапите
Крок 2:
Застосовуйте формулу 14.2 для визначення періодичної виплати відсотків за облігаціями.
Крок 3:
Визначте ціну покупки облігацій. Він відомий в $4 699,02 і його не потрібно розраховувати. Це дата ціна для кроку 5.
Крок 4:
Визначте ціну продажу облігацій, застосувавши формули 9.1, 11.1 та 14.3. Це майбутнє значення (\(FV\)) для кроку 5.
Крок 5:
Застосовуйте формули 11.1, 14.3 та 9.1 для визначення прибутковості інвестора (\(IY\)). Вирішіть формули 14.3 і 9.1 за допомогою калькулятора.
Виконувати
Крок 2:
\[PMT_{BOND}=\$ 5,000 \times \dfrac{0.05}{2}=\$ 125 \nonumber \]
Крок 4:
\(i=3.35 \% / 2=1.675 \% ; N=2 \times 10=20\)(сполуки та платежі)
\[\text { Date Price }=\dfrac{\$ 5,000}{(1+0.01675)^{20}}+\$ 125\left[\dfrac{1-\left[\dfrac{1}{1+0.01675}\right]^{20}}{0.01675}\right]=\$ 5,696.14 \nonumber \]
Крок 5:
\(N=2 \times 10=20 \)(сполуки та платежі)
\[\$ 4,699.02=\dfrac{\$ 5,696.14}{(1+i)^{20}}+\$ 125\left[\dfrac{1-\left[\dfrac{1}{1+i}\right]^{20}}{i}\right] \quad i=\dfrac{IY}{2} \nonumber \]
Вихід калькулятора\(=IY=6.8338 \%\)
Інструкції з калькулятора
| Крок | Режим | П | В/У | ПВ | PMT | ФВ | П/У | С/У |
|---|---|---|---|---|---|---|---|---|
| 4 | КІНЕЦЬ | 20 | 3.35 | Відповідь: 5 696.138252 | 125 | 5000 | 2 | 2 |
| 5 | \(\surd\) | \(\surd\) | Відповідь: 6.833820 | -4 699.02 | \(\surd\) | 5696.14 | \(\surd\) | \(\surd\) |
Ринкова ціна облігацій значно зросла протягом 10-річного періоду, оскільки ринкова ставка знизилася з 5,5% до 3,35%. Таким чином, інвестор реалізує більше, ніж початкова прибутковість до погашення на 5,5% (ринкова ставка), а фактично прибутковість інвестора зросла до 6,8338% в сукупності півріччя.
