14.1: Визначення вартості облігації
- Page ID
- 66720
Саме те, що коштує ваша товарна облігація? Коли ви оглядаєте фінансовий розділ вашої місцевої газети, ви звертаєте особливу увагу на котирування облігацій, в які ви вклали частину свого портфеля RRSP. Десять років тому, коли переважаючі ставки облігацій становили 5,5%, ви придбали 10 Уряд Канади $5,000 номінальної вартості облігацій з 5% купоном і 20 років, що залишилися до погашення. У той час, коли ви заплатили $4,699,02 кожен за них. Сьогоднішні ставки облігацій знизилися до 3,35%, але, як очікується, зростуть найближчим часом. Ви повинні триматися за ці облігації? Ви повинні перевести їх в готівку, продаючи їх на ринку облігацій?
Щоб допомогти відповісти на ці питання, дуже важливо знати вартість або ціну продажу ваших облігацій сьогодні. У цьому розділі пояснюється поняття товарної облігації разом з її важливими характеристиками та термінологією. Ви розраховуєте ціну продажу облігацій спочатку на дати виплати відсотків, а потім на всі інші дати, які представляють більш складну ситуацію.
Основи облігацій
Ринкова облігація, як показано на фотографії, - це борг, який забезпечений певним корпоративним активом і який встановлює відповідальність емітента перед кредитором за виплату відсотків через рівні проміжки часу та погашення основного боргу у встановлений більш пізній термін. Боргові зобов'язання - це те саме, що товарна облігація, за винятком того, що борг не забезпечений будь-яким конкретним корпоративним активом. Математично розрахунки ідентичні для цих двох фінансових інструментів, які цей підручник називає облігаціями для простоти. Типова шкала облігацій виглядає так, як показано нижче. Також обговорюються ключові терміни.

Дата випуску облігацій
Дата випуску облігацій - це дата, коли облігація випущена та доступна для придбання кредиторами. Відсотки нараховуються з цієї дати.
Номінальна вартість облігацій
Також називається номінальною вартістю або номіналом облігації, номінал облігації є основною сумою боргу. Це те, що інвестор позичив корпорації-емітенту облігацій. Сума, як правило, кратна 100 доларів, зустрічається невеликими номіналами до 10 000 доларів для індивідуальних інвесторів та більшими номіналами до 50 000 доларів або більше для корпоративних інвесторів.
Ставка купона облігацій
Також відома як ставка облігацій або номінальна ставка, купонна ставка облігацій - це номінальна процентна ставка, що виплачується за номіналом облігації. Ставка купона фіксується на термін дії облігації. Найчастіше відсотки нараховуються піврічно і підлягають сплаті в кінці кожного шестимісячного періоду протягом усього терміну дії облігації, починаючи з дати випуску. Усі купонні ставки, що використовуються в цьому підручнику, можна вважати, що вони складаються піврічно, якщо не вказано інше.
Ринкова ставка облігацій
Ринкова ставка облігацій - це переважна номінальна процентна ставка на відкритому ринку облігацій. Оскільки облігації активно торгуються, ця ставка коливається виходячи з економічних і фінансових умов. На дату випуску ринкова ставка визначає купонну ставку, яка прив'язана до облігації. Ринкові ставки зазвичай складаються півроку, як передбачається в цьому підручнику, якщо не вказано інше. Тому товарні облігації утворюють звичайні прості ануїтети, так як процентні виплати і ринкова ставка одночасно ускладнюються півроку, а виплати відбуваються в кінці інтервалу.
Ціна погашення облігацій
Також називається вартістю погашення або вартістю погашення, ціна викупу облігацій - це сума, яку емітент облігацій заплатить власнику облігацій після погашення облігації. Ціна викупу зазвичай дорівнює номіналу облігації, і в цьому випадку облігація вважається «погашеним номіналом», оскільки відсотки по облігації вже виплачувалися повністю періодично протягом усього терміну, залишаючи лише основну суму на рахунку. У деяких випадках емітент облігацій може фактично викупити облігацію з премією, яка є ціною, більшою за номінал. Потім ціна викупу вказується у відсотках від номіналу, наприклад 103%. Для вступних цілей цей текст дотримується найбільш поширеної ситуації, коли ціна викупу дорівнює номіналу.
Дата погашення облігацій
Також відома як дата погашення або термін погашення, дата погашення облігацій - це день, коли ціна погашення буде виплачена держателю облігацій (разом із остаточною виплатою відсотків), тим самим гасячи борг.
Дата продажу облігацій
Дата, коли облігація активно торгується та продається іншому інвестору через ринок облігацій, відома як дата продажу облігацій. На часовій шкалі дата продажу може відображатися будь-де на часовій шкалі між датою випуску та датою погашення, і це може відбуватися більше одного разу, коли облігація продається одним інвестором за іншим.
Розрахунок ціни облігації на дату виплати відсотків
Ринкові облігації та боргові зобов'язання не підлягають погашенню, а це означає, що єдиний спосіб перевести в готівку ці облігації до дати погашення - продати їх іншому інвестору. Тому ключовим математичним розрахунком є те, що платити за облігацію. Дата продажу, дата погашення, купонна ставка, ціна погашення та ринкова ставка разом визначають ціну облігації. На дату випуску облігацій ринкова ставка визначає купонну ставку, тому ці дві ставки ідентичні. В результаті ціна облігації дорівнює її номіналу. Після випуску облігації на неї починають нараховуватися відсотки, а ринкова ставка починає коливатися виходячи з кон'юнктури ринку. Це змінює ціну облігації.
Формула
Оскільки облігація виплачує відсотки піврічно, два дні року визначаються як дати виплати відсотків. Щоб визначити ціну продажу облігації в ці два дні, ви повинні використовувати формули для поточної вартості звичайної ануїтету. Як тільки ви зрозумієте, як виконати ці основні розрахунки, ми перейдемо до більш складних формул і прийомів, необхідних для визначення ціни продажу в інші 363 дні року. Незалежно від дати продажу, Формула 14.1 висловлює, як визначити ціну будь-якої облігації.

Щоб визначити ціну продажу облігації, ви повинні знати суму піврічної виплати відсотків держателю облігацій. Ви використовуєте Формулу 14.2, щоб розрахувати цю суму.

Ринкова ціна облігації на дату її продажу - це поточна вартість всіх майбутніх грошових потоків, як показано на малюнку нижче. Для покупця облігацій це комбінація решти купонних ануїтетних платежів плюс ціна викупу в кінці терміну (яка в цьому підручнику завжди дорівнює номіналу). Формула 14.3 підсумовує цей розрахунок, який об'єднує формули 9.3 і 11.4 разом і спрощує отриманий вираз.
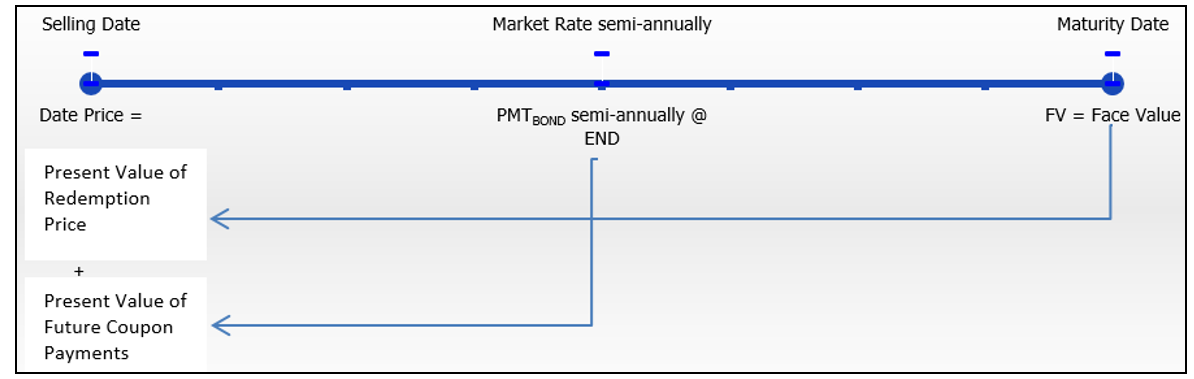
Ціна облігації коливається з ринковим курсом з плином часу. Якщо облігація продається за ціною, що перевищує її номінал, різниця відома як премія за облігацію. Якщо облігація продається за ціною, нижчою за її номінал, різниця відома як знижка на облігації. Сума премії або знижки виключає будь-які нараховані відсотки за облігацією. Чому ціна продажу змінюється так? Пам'ятайте, що відсотки, що виплачуються облігацією, - це фіксована ставка (купонна ставка), визначена на момент випуску.
• Припустимо купонну ставку 5%. Якщо ринкова ставка зросла до 6%, це означає, що інвестори можуть купувати облігації, сплачуючи 6%. Якщо ви намагаєтеся продати свою 5% облігацію, ніхто не хоче купувати її, якщо ви не «продаєте» у сумі, яка компенсує різницю в 1%. Отже, ви знижуєте свою облігацію.
• Крім того, якщо ринкова ставка знижується до 4%, це означає, що інвестори можуть купувати облігації, сплачуючи 4%. Якщо ви намагаєтеся продати свою 5% облігацію, це дуже привабливо для інвесторів, тому ви додаєте додаткову маржу, підвищуючи ціну на суму, що не перевищує 1% різниці. Отже, ви продаєте за преміальною ціною.
Цифра після Формули 14.3 ілюструє взаємозв'язок між ринковою ставкою, ставкою купона та ціною продажу облігації. Зверніть увагу, що коли купонна ставка вище ринкової, ціна продажу піднімається вище своєї номіналу. Крім того, коли купонна ставка нижча за ринкову, ціна продажу опускається нижче її номіналу. Застосовуйте Формулу 14.4, щоб розрахувати суму премії або знижки за облігацією.

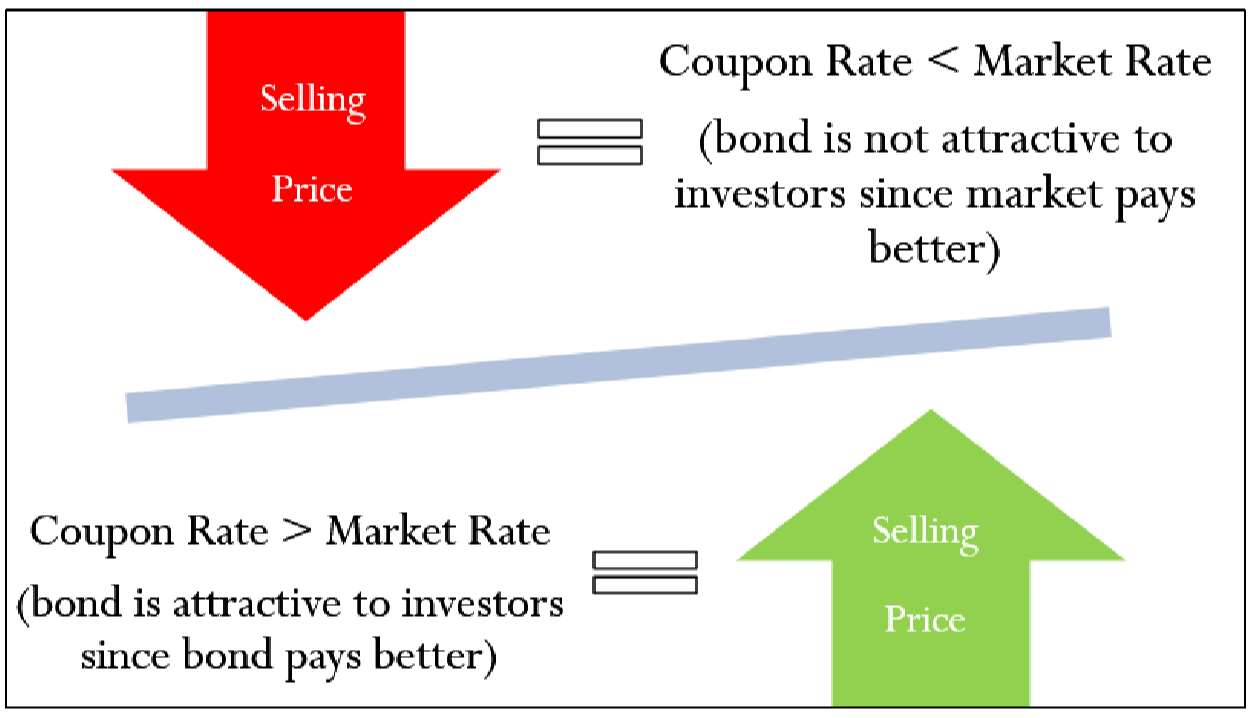

Як це працює
Виконайте наступні дії, щоб розрахувати ціну облігації на дату виплати відсотків:
Крок 1: Намалюйте часову шкалу, що триває від дати продажу до дати погашення. Визначте всі відомі змінні.
Крок 2: Використовуючи формулу 14.2, розрахуйте суму регулярної виплати відсотків за облігаціями. Для майбутніх розрахунків не округляйте це число.
Крок 3: Використовуючи формулу 14.3, розрахуйте ціну дати облігації. На дату виплати відсотків ціна дати дорівнює як ринковій, так і грошовій ціні.
- Використовуйте ринкову ставку для Формули 9.1 (Періодична процентна ставка).
- Як правило, для розрахунку N вам потрібно як Формула 9.2 (Кількість складених періодів для разових платежів) для вартості викупу, так і Формула 11.1 (Кількість ануїтетних платежів) для ануїтету. Однак, оскільки складені періоди та ануїтетні платежі є як піврічними, то кожна формула буде виробляти однакове значення\(N\). Таким чином, ви можете використовувати тільки Формулу 11.1, визнаючи, що вона представляє як кількість складних періодів, так і кількість ануїтетних платежів.
- Ціна дати від Формули 14.3 дорівнює ринковій ціні. Оскільки нарахованих відсотків немає, готівкова ціна така ж, як і ціна дати.
Крок 4: Якщо потрібно, використовуйте Формулу 14.4 для розрахунку будь-якої премії або знижки за облігації.
Важливі зауваження
Функція БОНД на калькуляторі BAII Plus. На дату виплати відсотків, ви можете вирішити будь-яку проблему облігацій за допомогою регулярного часу вартості грошей кнопки на калькуляторі, оскільки облігації представляють собою звичайні прості ануїтети. Однак вбудована функція для облігацій на калькуляторі BAII Plus значно спрощує розрахунки цін на облігації, особливо коли облігація продається на дату, відмінну від дати виплати відсотків. Функція BOND розташована на другій полиці над клавішею цифри 9 і доступна натисканням 2nd BOND.

Ця електронна таблиця містить дев'ять рядків, які ви прокручуєте за допомогою стрілок ↓ і ↑. Перші сім рядків вважаються рядками введення даних, а останні два - вихідними. Відкривши вікно, слід скористатися 2-й функцією CLR Work, щоб стерти раніше завантажені дані. Рядки введення даних такі:
- SDT - дата продажу. Він вводиться в стандартному форматі дати MM.DDYY, де MM - номер місяця (одна або дві цифри), DD - двозначний номер дня, а YY - дві останні цифри року. Ви повинні натиснути клавішу ENTER, щоб зберегти цю інформацію. Якщо питання не стосується конкретних дат, використовуйте 1 січня 2000 року або 1.0100, щоб легше визначити дату викупу.
- CPN - номінальна купонна ставка. Він відформатований у відсотках, але без знака відсотка; таким чином, 5.5% вводиться як 5.5. Ви повинні натиснути клавішу ENTER, щоб зберегти цю інформацію.
- RDT - дата погашення або дата погашення. Вона повинна бути введена в стандартному форматі дати, і ви повинні натиснути ENTER, щоб зберегти цю інформацію. Якщо питання не стосується конкретних дат, вкажіть відповідну дату на основі дати продажу 1 січня 2000 року.
- RV - це вартість викупу або ціна викупу, виражена у відсотках від номіналу. Оскільки ціна викупу дорівнює номіналу, використовуйте значення за замовчуванням 100. Цей підручник ніколи не вимагає від вас змінити це число.
- ACT/360 - це перемикач, який ви змінюєте, натиснувши 2nd SET. ACT підраховує фактичну кількість днів у транзакції, тоді як 360 розглядає щомісяця як 30 днів. У Канаді ACT є стандартом, тому вам слід залишити калькулятор на цьому налаштуванні.
- 2/Y АБО 1/Y - це перемикач, який ви змінюєте, натиснувши 2nd SET. 2/Y вказує на піврічне з'єднання як для ринкової ставки, так і для ставки купона, тоді як 1/Y вказує на річне з'єднання. Цей підручник завжди використовує налаштування 2/Y.
- YLD - номінальна ринкова ставка облігацій на момент продажу. Він слідує тому ж формату, що і CPN, тобто відсоток, але без знака відсотка. Ви повинні натиснути клавішу ENTER, щоб зберегти інформацію. Вихідні рядки такі:
- PRI - ринкова ціна облігації. Після прокрутки до цього рядка натисніть кнопку CPT, щоб обчислити цей висновок, який не обчислюється автоматично. Вихід - відсоток від ціни викупу (який збігається з номіналом). Таким чином, якщо у вас є облігація номінальної вартості 1000 доларів, вам потрібно взяти вихід, розділений на 100 помножений на номінал, щоб прийти до ринкової ціни.
- AI - нараховані відсотки по облігації. Цей результат автоматично обчислюється при натисканні кнопки CPT на рядку PRI. Якщо ви перебуваєте на даті виплати відсотків, вона має нульове значення. Якщо ви перебуваєте між платежами, результат, як і PRI, становить відсоток від ціни викупу, тому вам потрібно конвертувати його у значення таким же чином, як і PRI.
Якщо вас цікавить грошова ціна облігації, ви повинні скласти разом значення, пов'язані з виходами PRI та AI, як у Формулі 14.1. Коли ви закінчите з функцією BOND, натисніть 2nd QUIT, щоб залишити вікно.
Речі, на які слід остерігатися
Коли ви розраховуєте ціну облігації на дату виплати відсотків, ціна дати фактично обчислює ринкову ціну. Нагадаємо, що грошова ціна облігації завжди визначається Формулою 14.1, де ринкова ціна та нараховані відсотки повинні бути підсумовані, щоб прийти до грошової ціни. На дати виплати відсотків нараховані відсотки відсутні, тому він завжди має значення нуля. Працюючи з облігаціями, увійдіть в звичку тепер мислити на манер Формули 14.1. Пізніше, коли облігація продається на дату платежу без відсотків і беруть участь нараховані відсотки, ця звичка зручна для з'ясування цін на облігації. Що стосується калькулятора BAII Plus, завжди додавайте разом виходи вікон PRI та AI, щоб досягти ціни продажу (готівкової ціни) облігації.
Шляхи до успіху
Раніше в цьому підручнику обговорювалися ощадні облігації Канади. Зверніть увагу, що ці облігації можна повністю погасити в будь-який момент, оскільки ви можете перевести їх у готівку в будь-який момент у будь-якій фінансовій установі до погашення. Тому ощадні облігації Канади не вважаються товарними облігаціями і не діють відповідно до принципів, розглянутих у цьому розділі.
- Поясніть взаємозв'язок між змінами ринкової ставки облігацій і ціною облігації.
- Які п'ять змінних використовуються при визначенні ціни облігації?
- Правда чи помилково: Якщо облігація номінальної вартості 1,000 доларів має готівкову ціну 1,125 доларів та ринкову ціну 1100 доларів, вона продається за премією за облігацію в розмірі 100 доларів США.
- Які три змінні визначають суму купонного платежу?
- Відповідь
-
- У міру зростання ринкової ставки ціна облігацій знижується, і навпаки.
- Дата продажу, дата погашення, купонна ставка, ціна погашення та ринкова ставка
- Правда; премія за облігації - це різниця між номіналом і ринковою ціною.
- Номінальна вартість, номінальна купонна ставка та частота складання купонної ставки; див. Формулу 14.2
Уряд Канади $50,000 облігації був випущений 15 січня 1991 року, з 25-річним терміном погашення. Купонна ставка становила 10,15%, що збільшується півріччя. Яку готівкову ціну мали облігації 15 липня 2005 року, коли переважаючі ринкові ставки становили 4.31%, що складаються півроку? Якою була сума премії або знижки за облігації?
Рішення
Ця облігація здійснює виплату відсотків з інтервалом шість місяців, 15 січня та 15 липня щороку. Облігація продається 15 липня, що є датою виплати відсотків. На дату виплати відсотків вирішіть ціну дати, яка така ж, як і готівкова ціна. Також розрахуйте премію або знижку.
Що ви вже знаєте
Крок 1:
Графік продажу облігацій відображається нижче.
Виплата купонного\(CPN\) відсотка: = 10,15%,\(CY\) = 2, номінал = $50,000
Облігація:\(FV\) = $50,000,\(IY\)\(CY\) = 4,31%,\(PMT_{BOND}\) = 2, = Формула 14.2,\(PY\) = 2, роки залишилися = 10,5
Як ви туди потрапите
Крок 2:
Застосовуйте формулу 14.2 для визначення періодичної виплати відсотків за облігаціями.
Крок 3:
Застосовуйте формули 9.1, 11.1 та 14.3 для визначення ціни облігації на дату її виплати відсотків. Грошова ціна у Формулі 14.1 дорівнює ціні дати.
Крок 4:
Застосуйте Формулу 14.4, щоб визначити премію або знижку за облігацію.
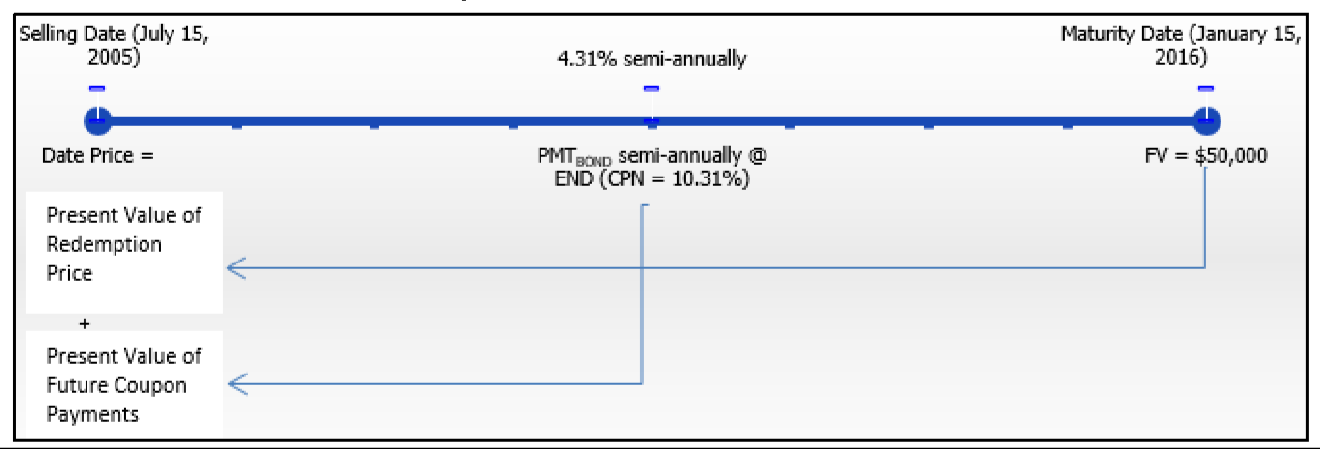
Виконувати
Крок 2:
\[PMT_{BOND}=\$ 50,000 \times \dfrac{0.1015}{2}=\$ 50,000 \times 0.05075=\$ 2,537.50 \nonumber \]
Крок 3:
\(i=4.31 \% / 2=2.155 \% ; N=2 \times 10.5=21\)(сполуки та платежі)
\[\text { Date Price }=\dfrac{\$ 50,000}{(1+0.02155)^{21}}+\$ 2,537.50\left[\dfrac{1-\left[\frac{1}{1+0.02155}\right]^{21}}{0.02155}\right]=\$ 74,452.86 \nonumber \]
Крок 4:
Преміум або знижка\(=\$ 74,452.86-\$ 50,000.00=\$ 24,452.86\)
Інструкції з калькулятора
| SDT | КПН | РДТ | РВ | Дні | З'єднання | ЙЛД | ПРИ | АЙ |
|---|---|---|---|---|---|---|---|---|
| 7.1505 | 10.15 | 1.1516 | 100 | АКТ | 2/Г | 4.31 | Відповідь: 148.905720 | Відповідь: 0 |
Трансформація виведення:
\[\dfrac{148.905720+0}{100} \times \$ 50,000=\$ 74,452.86012 \nonumber \]
Облігація має купонну ставку, яка значно вища за ринкову ставку, тому вона продається з премією в розмірі $24,452.86 за готівкову ціну $74,452.86. Зверніть увагу, що оскільки продаж відбувається на дату виплати відсотків, нараховані відсотки відсутні, тому ринкова ціна та ціна готівки однакові.
Облігація уряду Канади в розмірі 25 000 доларів США була випущена з 25-річним терміном погашення та купонною ставкою 8.92%, що складається піврічно. Через два з половиною роки облігація продається, коли ринкові ставки зросли до 9,46%, що посилюється піврічно. Визначте ціну продажу облігації разом із сумою премії або знижки.
Рішення
Хоча конкретних дат немає, купон є піврічним, здійснюючи виплати відсотків кожні півроку. Якщо облігація продається через 2½ роки після випуску, це робить дату продажу датою виплати відсотків. На дату виплати відсотків вирішіть ціну дати, яка така ж, як і готівкова ціна. Також розрахуйте премію або знижку.
Що ви вже знаєте
Крок 1:
Графік продажу облігацій відображається нижче.
Виплата купонного\(CPN\) відсотка: = 8.92%,\(CY\) = 2, номінал = $25,000
Облігація:\(FV\) = 25 000 доларів,\(IY\) = 9,46%,\(CY\) = 2,\(PMT_{BOND}\) = Формула 14.2,\(PY\) = 2, роки залишилися = 22,5
Як ви туди потрапите
Крок 2:
Застосовуйте формулу 14.2 для визначення періодичної виплати відсотків за облігаціями.
Крок 3:
Застосовуйте формули 9.1, 11.1 та 14.3 для визначення ціни облігації на дату її виплати відсотків. Грошова ціна у Формулі 14.1 дорівнює ціні дати.
Крок 4:
Застосуйте Формулу 14.4, щоб визначити премію або знижку за облігацію.
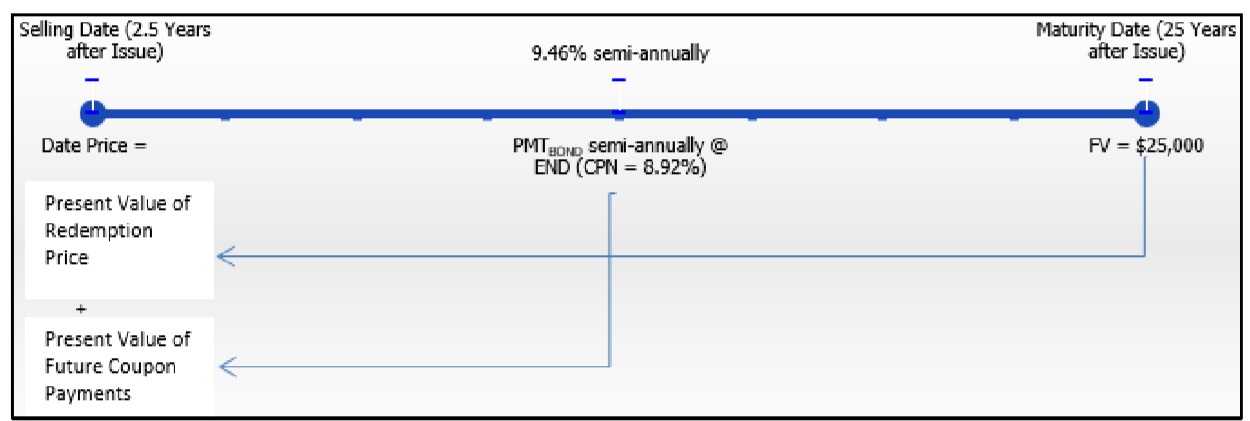
Виконувати
Крок 2:
\[PMT_{BOND}=\$ 25,000 \times \dfrac{0.0892}{2}=\$ 25,000 \times 0.0446=\$ 1,115 \nonumber \]
Крок 3:
\(i=9.46 \% / 2=4.73 \% ; N=2 \times 22.5=45\)(сполуки та платежі)
\[\text { Date Price }=\dfrac{\$ 25,000}{(1+0.0473)^{45}}+\$ 1,115\left[\dfrac{1-\left[\dfrac{1}{1+0.0473}\right]^{45}}{0.0473}\right]=\$ 23,751.28 \nonumber \]
Крок 4:
Преміум або знижка\(=\$ 23,751.28-\$ 25,000.00=-\$ 1,248.72\)
Інструкції з калькулятора
| SDT | КПН | РДТ | РВ | Дні | З'єднання | ЙЛД | ПРИ | АЙ |
|---|---|---|---|---|---|---|---|---|
| 1.0100 | 8.92 | 7.0122 | 100 | АКТ | 2/Г | 9.46 | Відповідь: 95.005105 | Відповідь: 0 |
Трансформація виведення:
\[\dfrac{95.005105+0}{100} \times \$ 25,000=\$ 23,751.27631 \nonumber \]
Облігація має купонну ставку, яка трохи нижча за ринкову, тому вона продається зі знижкою в розмірі 1 248.72 доларів за готівкову ціну 23 751,28 долара. Зверніть увагу, що оскільки продаж відбувається на дату виплати відсотків, нараховані відсотки відсутні, тому ринкова ціна та ціна готівки однакові.
Розрахунок ціни облігації на дату невиплати відсотків
Є лише два дні року, коли готівкова ціна та ринкова ціна облігації однакові. Ті дні - дати виплати відсотків, коли ви визначаєте вартість облігації за формулою 14.3. Однак що станеться, якщо облігація буде продана в один з інших 363 днів року?
У ці інші дати готівкова ціна та ринкова ціна не рівні. За кожен день, який закінчується після дати виплати відсотків, відсотки за наступний платіж починають нараховуватися таким чином, щоб протягом наступних шести місяців було достатньо відсотків для здійснення наступної виплати відсотків.
Відповідно до Формули 14.1, коли інвестор хоче придбати облігацію між датами виплати відсотків, покупець повинен заплатити продавцю готівкову ціну, що дорівнює ринковій ціні облігації плюс нараховані відсотки. Чому? Припустимо, облігація здійснює піврічні виплати відсотків у розмірі 50 доларів. Коли покупець набуває облігацію у продавця, минуло два місяці з моменту останньої дати виплати відсотків. Оскільки продавець утримував облігацію протягом двох місяців шестимісячного інтервалу оплати, продавцю справедливо і розумно отримати відсотки, зароблені за цей період. Однак облігація не здійснить наступну виплату відсотків лише через чотири місяці, тоді покупець, який зараз володіє облігацією, отримає повну виплату відсотків у розмірі 50 доларів США протягом повних шести місяців. Таким чином, під час покупки облігації покупець повинен сплатити продавцеві ринкову ціну облігації плюс частину наступного платежу відсотків, яка юридично належить продавцю. У цьому прикладі потрібно виплатити процентну суму, що становить два з шести місяців.
Формула
Прибуття до ціни облігації між датами виплати відсотків є дещо складним, оскільки грошова ціна зростає за складною формулою відсотків, тоді як на практиці нараховані відсотки за облігацією збільшуються за простою формулою відсотків. Якщо це здається вам властивим, ви б мали рацію, але саме так трапляються зв'язки!
Вам потрібно три важливі частини інформації: що платити (готівкова ціна), скільки простих відсотків було включено в готівкову ціну (нараховані відсотки), і яка фактична вартість облігації (ринкова ціна). Щоб отримати ці три номери, виконайте наступні дії:
- Спочатку розрахуйте готівкову ціну облігації, як показано у Формулі 14.5.
- Розрахуйте нараховані відсотки, включені до цієї ціни, як показано у Формулі 14.6.
- Визначте ринкову ціну з Формули 14.1.


Як це працює
Виконайте наступні дії, щоб розрахувати ціну облігації між датами виплати відсотків:
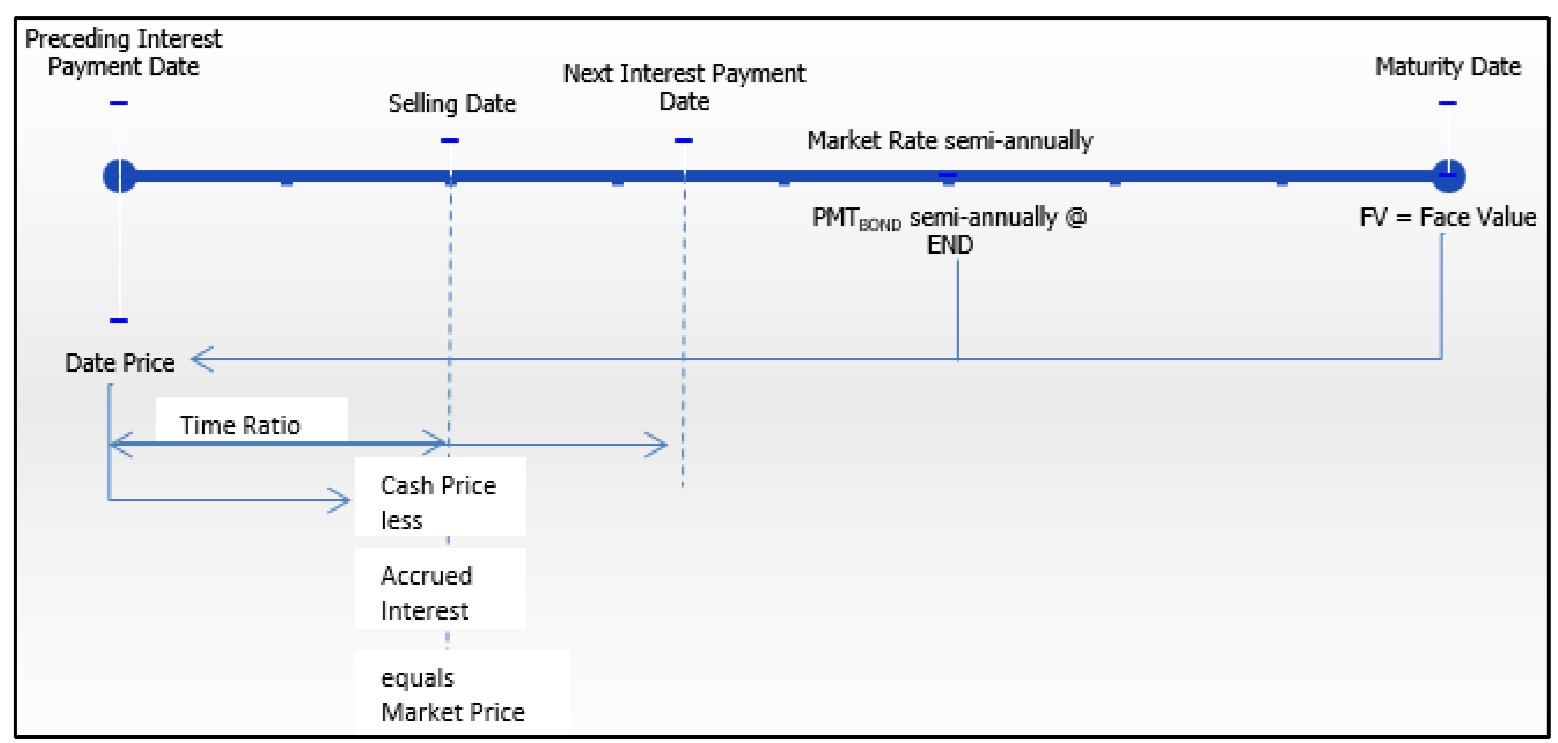
Крок 1: Намалюйте часову шкалу, подібну до тієї, що праворуч, починаючи від попередньої дати виплати відсотків до дати погашення. Визначте всі відомі змінні.
Крок 2: Використовуючи формулу 14.2, розрахуйте суму регулярної виплати відсотків за облігаціями. Для майбутніх розрахунків не округляйте це число.
Крок 3: Використовуючи формулу 14.3, розрахуйте ціну дати облігації на дату виплати відсотків, що передує даті продажу.
- Використовуйте ринкову ставку для Формули 9.1 (Періодична процентна ставка).
- Нагадаємо, що ви використовуєте тільки Формулу 11.1 і визнаєте, що вона представляє як кількість складних періодів, так і кількість ануїтетних платежів.
Крок 4: Розрахуйте готівкову ціну облігації за формулою 14.5. Розрахуйте коефіцієнт часу, визначивши точну кількість днів, які продавець утримував облігацію, а також точну кількість днів, задіяних у поточному інтервалі виплат.
Крок 5: Розрахуйте нараховані відсотки по облігації за формулою 14.6. Використовуйте співвідношення часу з кроку 5.
Крок 6: Розрахуйте ринкову ціну облігації за формулою 14.1.
Крок 7: Якщо потрібно, використовуйте Формулу 14.4 для розрахунку премії або знижки за облігацію.
Важливі зауваження
Функція DATE на калькуляторі BAII Plus. Щоб створити часовий коефіцієнт, визначте кількість днів з дати останньої виплати відсотків, а також загальну кількість днів у поточному інтервалі платежу. Обчислити це можна за допомогою функції DATE. Для повного обговорення цієї функції згадайте інструкції в кінці глави 8. Щоб прибути на необхідні номери:
- Обчисліть кількість днів з дати останньої виплати відсотків, ввівши дату останньої виплати відсотків як DT1, а дату продажу як DT2. Обчислити DBD.
- Обчисліть загальну кількість днів у поточному інтервалі платежу, ввівши дату останньої виплати відсотків як DT1, а наступну дату виплати відсотків як DT2. Обчислити DBD.
Речі, на які слід остерігатися
При розрахунках облігаційних премій і знижок на безвідсоткові дати виплат найпоширенішою помилкою є використання готівкової ціни замість ринкової. Пам'ятайте, що грошова ціна включає в себе як нараховані відсотки, так і ринкову ціну. Нараховані відсотки не враховуються на вартість облігації, оскільки він являє собою пропорцію наступної виплати відсотків між продавцем та покупцем. Тому сума облігаційної премії або дисконту не повинна включати нараховані відсотки. Використовуйте лише ринкову ціну для визначення премії або знижки.
Шляхи до успіху
На BAII Plus,\(PRI\) і\(AI\) виходи робочого аркуша BOND повинні бути підсумовані разом, щоб отримати готівкову ціну. Обидва ці виходи представляють відсоток від номіналу (тієї ж бази) і можуть бути підсумовані перед перетворенням відсотка в доларову суму. Наприклад, якщо\(PRI\) = 98% і\(AI\) = 2,5%, ви могли б взяти загальну суму 100,5%, щоб з'ясувати ціну готівки. Використовуючи калькулятор ефективно, ви зберігаєте їх\(PRI\) у комірці пам'яті, прокрутіть вниз, а потім додайте відкликання комірки пам'яті до того,\(AI\) щоб прийти до загального відсотка номіналу.
