6.1: Малюнки?

Last updated
Save as PDF

Page ID: 65679

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Всі тексти, про які йшлося вище, ілюструвалися геометричними малюнками. Однак лише дві таблетки несли геометричні схеми, і в обох випадках вони ілюстрували постановку проблеми, а не процедуру.

Багато аспектів процедур незрозумілі в традиційній арифметичній інтерпретації, але природно пояснюються геометричним читанням. отже, якась геометрія повинна брати участь у міркуваннях вавилонян. Однак не дуже правдоподібно, що вавилоняни використовували малюнки тихо, як наші. Навпаки, багато текстів дають нам підстави вважати, що вони були задоволені рудиментарними структурними діаграмами; див. Наприклад, стор. 52 про зміну масштабу в одному напрямку. Відсутність конкретних назв для\(L = 3\lambda\) і\(W = 21\phi\) в TMS IX #3 (див. Сторінка 59) також говорить про те, що не було створено жодної нової діаграми, в якій їх можна було б ідентифікувати, в той час як\(\lambda\) і можна\(\phi\) було б ідентифікувати як сторони «поверхні 2".

Адже це не дивно. Той, хто знайомий зі старими вавилонськими техніками, не потребуватиме нічого, крім грубого ескізу, щоб слідувати міркуванням; немає навіть необхідності виконувати поділи та зміщення, лише малюнок прямокутника дозволяє зрозуміти процедуру, яку потрібно використовувати. так само, як ми можемо виконати розумові обчислення, роблячи максимум нотаток для одного або двох проміжних результатів, ми також можемо ознайомитись з «ментальною геометрією», що найбільше допомагає груба діаграма.

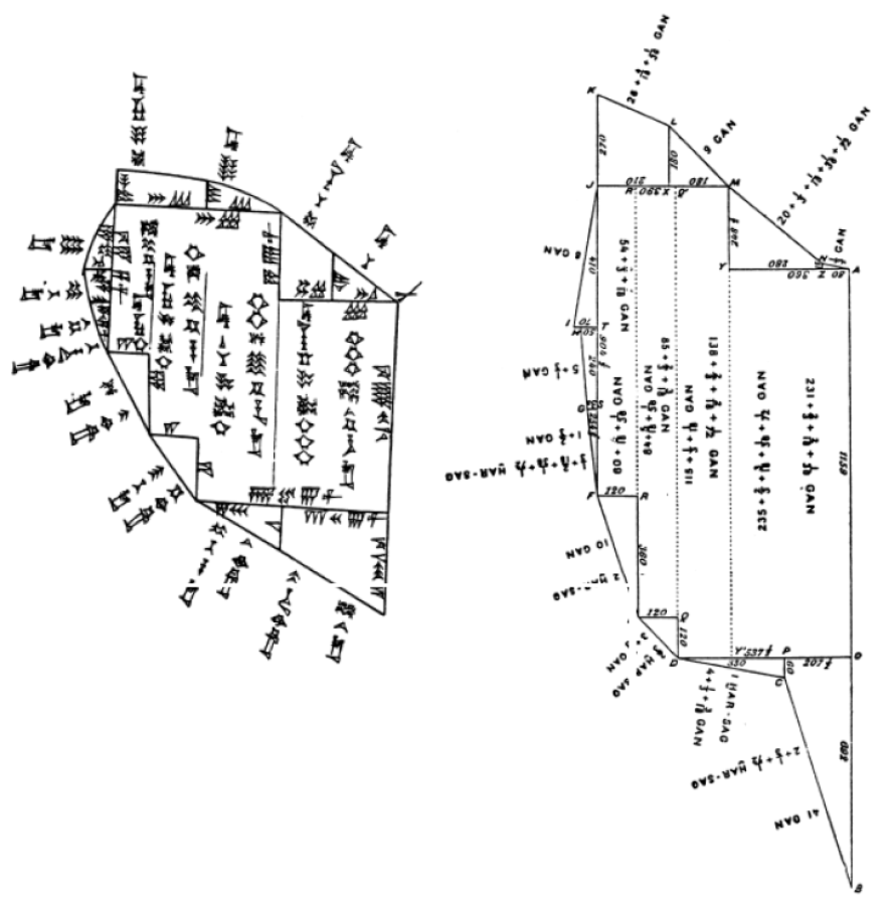
Збереглося неабияка кількість польових планів, зроблених месопотамськими книжниками; ліва частина малюнка 6.1 показує один з них. Вони мають саме характер структурних діаграм; вони не мають на меті бути вірними у візуалізації лінійних пропорцій, як буде видно, якщо порівняти з версією в правильних пропорціях праворуч. У цьому відношенні вони схожі на рисунок 4.5, справжні пропорції якого можна побачити на рис. 4.6 — сторінки 65 та 68 відповідно. Вони також не зацікавлені в тому, щоб правильно показувати кути, крім «практично прямих» кутів, які обслуговують розрахунки площі і тому мають структурну роль.

Малюнок\(6.1\): Нео-шумерський польовий план (21 століття до н.е.), зліва, як намальовано на планшеті, праворуч перемальований у правильних пропорціях Після F. Thureau-Dangin, «Un cadastre chaldéen». *Ревю д'Ассирологія* 4 (1897—98), 13—27.

Практика «ментальної геометрії» передбачає, що людина вперше навчила конкретну геометрію; таким чином, повинні існувати справжні малюнки. Однак операції вирізання та вставки нелегко зробити на глиняній таблетці. Пил абакус, використовуваний фінікійськими калькуляторами в першому тисячолітті до н.е., а потім перейнятий грецькими геометрами, ¹ набагато зручніше для цієї мети. Тут легко скасувати частину фігури і перемалювати її в новому положенні. Шкільний двір, усипаний піском (див. Сторінка 33) також був би зручним.

Таким же чином пил або пісок, здається, служили на перших кроках вивчення сценарію. З цієї початкової фази ми знаємо таблички, на яких вписані моделі, які повинні були відтворити учні, щоб вивчити клинописні символи. З наступного етапу ми також маємо глиняні таблички, написані студентами, але з першого етапу робота студентів не залишила археологічних слідів, а це означає, що вони, ймовірно, були намальовані піском або пилом. Тому немає підстав дивуватися тому, що геометричні малюнки з навчання алгебри та квазіалгебри не знайдені.