15.3: Пошук наборів еквівалентності

Формальне визначення говорить, що два актори регулярно еквівалентні, якщо вони мають схожі моделі зв'язків з еквівалентними іншими. Розглянемо двох чоловіків. У кожного є діти (хоча вони мають різну кількість дітей, і, очевидно, мають різних дітей). У кожного є дружина (хоча знову ж таки, зазвичай різні особи заповнюють цю роль по відношенню до кожного чоловіка). У кожної дружини, в свою чергу, теж є діти і чоловік (тобто вони мають зв'язки з одним або декількома членами кожного з цих наборів). Кожна дитина має зв'язки з одним або декількома членами безлічі «чоловіків» і «дружин».

Визначаючи, які актори є «чоловіками», ми не дбаємо про зв'язки між членами цього набору (насправді, ми очікуємо, що цей блок буде нульовим блоком, але нам насправді все одно). Що важливо, щоб кожен «чоловік» мав хоча б одну краватку з людиною в категорії «дружина» і хоча б одній людині в категорії «дитина». Тобто чоловіки рівноцінні один одному тому, що кожен має схожі зв'язки з якимось членом наборів дружин і дітей.

Але, здавалося б, проблема з цим досить простим визначенням. Якщо визначення кожної позиції залежить від її відносин з іншими позиціями, з чого почати?

Існує ряд алгоритмів, які допомагають ідентифікувати регулярні набори еквівалентності. UCINET надає деякі методи, які особливо корисні для знаходження приблизно регулярно еквівалентних акторів у цінних, багатореляційних та спрямованих графах. Деякі простіші методи для двійкових даних можна проілюструвати безпосередньо.

Розглянемо, знову ж таки, на прикладі мережі Вассермана-Фауста. Уявіть собі, однак, що це картина віддання наказів у простій ієрархії. Тобто всі стяжки спрямовані зверху діаграми на малюнку 15.1 вниз. Ми знайдемо регулярну характеристику еквівалентності цього графіка.

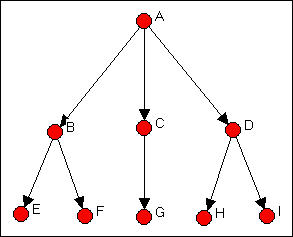
Малюнок 15.1: Направлена краватка версії мережі Вассермана-Фауста

Для першого кроку охарактеризуйте кожен вузол як або «джерело» (актор, який посилає зв'язки, але не отримує їх), «ретранслятор» (актор, який одночасно повторює і посилає), або «потопає» (актор, який отримує зв'язки, але не надсилає їх). Джерелом є A; ретранслятори - B, C і D; а раковини - E, F, G, H і I. Є четверта логічна можливість. «Ізолят» - це вузол, який ні посилає, ні отримує зв'язки. Ізоляти утворюють регулярний набір еквівалентності в будь-якій мережі і повинні бути виключені з регулярного аналізу еквівалентності підключеного підграфа.

Оскільки в наборі відправників є лише один актор, ми не можемо виявити жодної подальшої складності в цій «ролі».

Розглянемо три «ретранслятора» B, C і D. По сусідству (тобто поруч з) актора Б знаходяться як «джерела», так і «раковини». Те ж саме стосується «ретрансляторів» C і D, хоча три актори можуть мати різну кількість джерел і раковин, і це можуть бути різні (або однакові) конкретні джерела та раковини. Ми не можемо далі визначити «роль» множини {B, C, D}, тому що ми вичерпали їх околиці. Тобто джерела, до яких підключені наші ретранслятори, не можна додатково диференціювати на кілька типів (оскільки є лише одне джерело); раковини, до яких надсилають наші ретранслятори, не можуть бути додатково диференційовані, оскільки вони самі не мають додаткових з'єднань.

Тепер розглянемо наші «раковини» (тобто актори E, F, G, H і I). Кожен підключений до джерела (хоча джерела можуть бути різними). У поточному випадку ми вже визначили, що всі ці джерела (актори B, C та D) регулярно еквівалентні. Так, Е через I еквівалентно пов'язані з еквівалентними іншими. Ми закінчили з нашим розбиттям.

Результат {A} {B, C, D} {E, F, G, H, I} задовольняє умові, що кожен актор у кожному розділі має однакову схему зв'язків з акторами в інших розділах. Переставлена матриця суміжності показана на малюнку 15.2.

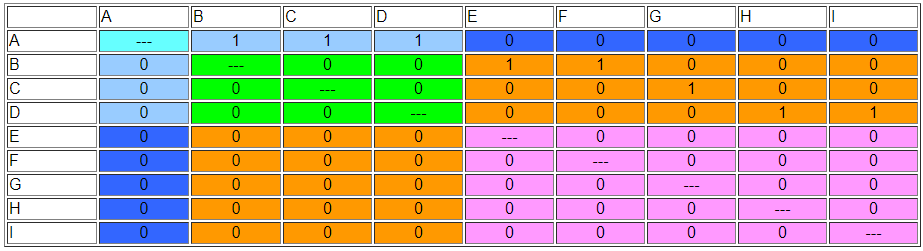
Малюнок 15.2: Перестановлена мережа Вассермана-Фауста, щоб показати регулярні класи еквівалентності

Корисно заблокувати цю матрицю і показати її зображення. Тут, правда, ми будемо використовувати деякі спеціальні правила визначення нульового і 1 блоку. Якщо блок - це всі нулі, це буде нульовий блок. Якщо кожен актор в розділі має прив'язку до будь-якого актора в іншому, то ми визначимо спільний блок як 1-блок. Неси зі мною хвилинку. Зображення з використанням цього правила показано на малюнку 15.3.

Малюнок 15.3: Блокове зображення регулярних класів еквівалентності в спрямованій мережі Вассермана-Фауста

{A} надсилає до одного або декількох з {BCD}, але жодному з {EFGHI}. {BCD} не надсилає {A}, але кожен з {BCD} надсилає принаймні одному з {EFGHI}. Жоден з {EFGHI} не надсилає жодному з {A} або {BCD}. Зображення, по суті, відображає характерну закономірність суворої ієрархії: одиниці на першому позадіагональному векторі і нулі в іншому місці. Правило визначення 1-блоку, коли кожен актор в одному розділі має зв'язок з будь-яким актором в іншому розділі є способом операціоналізації уявлення про те, що актори в першому наборі еквівалентні, якщо вони пов'язані з еквівалентними акторами (тобто акторами в іншому розділі), не вимагаючи (або забороняє), щоб вони були прив'язані до тих же інших акторів, або стільки ж акторів в іншому розділі.

Для спрямованих двійкових графів метод пошуку по сусідству, який ми застосували тут, зазвичай працює досить добре. Для двійкових графів, які не спрямовані, зазвичай обчислюється геодезична відстань між акторами і використовується замість сирої суміжності. Для графіків з ціннісними співвідношеннями (міцність, вартість, ймовірність) був розроблений метод ідентифікації приблизної регулярної еквівалентності Уайта і Рейца. Ці кілька альтернатив проілюстровані нижче.

Категоричний REGE для спрямованих двійкових даних (Wasserman-Faust спрямована мережа)

Метод пошуку околиць, проілюстрований вище (з спрямованою мережею Вассермана-Фауста) - це алгоритм, який виконується Мережа>Ролі та позиції>Максимальний регулярний>CatRege. Такий підхід ідеально підходить для мереж, де відносини вимірюються на номінальному рівні, і спрямовані. Наш приклад буде двійковим графом; Алгоритм, однак, також може мати справу з багатозначними номінальними даними (наприклад, «1" = друг, «2" = кін, «3" = колега тощо).

Застосування мережі>Ролі та позиції>Максимальний регулярний>Catrege до мережі, спрямованої Wasserman-Faust, дає результати, показані на малюнку 15.4.

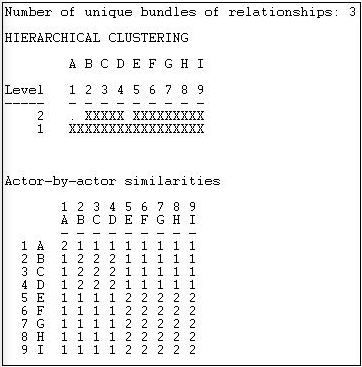
Малюнок 15.4: Категоричний аналіз REGE мережі, спрямованої Вассермана-Фауста

Цей результат такий же, як той, який ми робили «вручну» раніше в розділі. Ієрархічна схема кластеризації може бути корисною, якщо знайдені еквіваленти неточні або численні, і необхідне подальше спрощення. Тут ми бачимо на рівні 2 кластеризації, що існує три групи {A}, {B, C, D} і {E, F, G, H, I}. Також проводиться матриця зображення (але не «зменшується» до 3 на 3).

Результати також можна корисно візуалізувати за допомогою дендограми, як на малюнку 15.5.

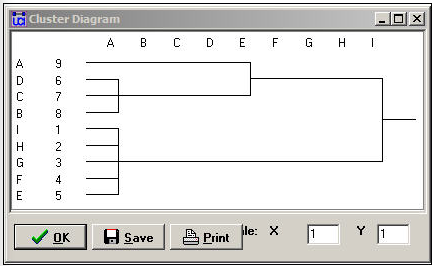
Малюнок 15.5: Дендограма категоріального РЕГЕ (рис. 15.4)

З нашого аналізу ми знаємо, що насправді існує рівно три регулярні класи еквівалентності. Якщо ми хочемо використовувати лише два, однак дендограма припускає, що групування A з B, C та D було б найбільш розумним вибором.

Після того, як було досягнуто регулярного блокування еквівалентності, зазвичай є гарною ідеєю створити перестановлену та заблоковану версію вихідних даних, щоб ви могли бачити профілі зв'язків кожного з класів. Один із способів зробити це - зберегти вектор перестановки з Мережі> Ролі та позиції> Максимальний регулярний> CatRege, і використовувати його для перемикання вихідних даних (Data> Permute).

Категоричний REGE для геодезичних відстаней (дані про шлюб Паджетта)

Дані Паджетта про шлюбні союзи між провідними флорентійськими сім'ями мають низьку та помірну щільність. Існують значні відмінності між положеннями сімейств, як видно з графіка на малюнку 15.6. Дані є двійковими, а не спрямованими. Це викликає проблему для регулярного аналізу еквівалентності, оскільки всі актори (крім ізолятів) є «еквівалентними» як «передавачі».

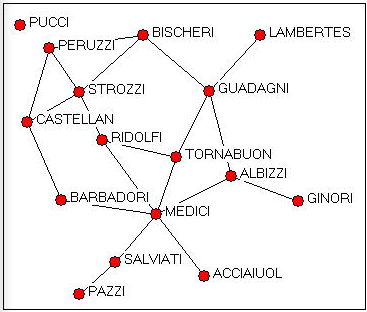
Малюнок 15.6: Паджетт Флорентійські шлюбні союзи

Категоричний алгоритм REGE (Мережа>Ролі та позиції>Максимальний регулярний>Catrege) може бути використаний для ідентифікації регулярно еквівалентних акторів шляхом розгляду елементів матриці геодезичної відстані як опису «типів» зв'язків - тобто різні геодезичні відстані розглядаються як» якісно», а не «кількісно» відрізняється. Два вузли більш еквівалентні, якщо кожен з них має актора в своєму районі одного і того ж «типу». У цьому випадку це означає, що вони схожі, якщо у кожного є актор, який знаходиться на однаковій геодезичній відстані від себе. При багатьох наборах даних рівні подібності кварталів можуть виявитися досить високими - і диференціювати позиції акторів на «регулярних» ознаках еквівалентності може бути важко.

На малюнку 15.7 показані результати регулярного аналізу еквівалентності, де геодезичні відстані були використані для представлення декількох якісних типів відносин між суб'єктами.

Малюнок 15.7: Категоричний багатозначний аналіз (геодезична відстань) шлюбних альянсів Паджетта

Оскільки дані дуже пов'язані, а геодезичні відстані короткі, ми не можемо розрізнити високохарактерні регулярні класи в цих даних. Дві сім'ї (Albizzi та Ridolfi) виникають як більш схожі, ніж інші, але, як правило, відмінності між профілями невеликі.

Використання REGE з неспрямованими даними, навіть підставляючи геодезичні відстані двійковими значеннями, може дати досить несподівані результати. Може бути корисніше об'єднати ряд різних зв'язків для отримання безперервних значень. Основна проблема, однак, полягає в тому, що з неспрямованими даними більшість випадків будуть здаватися дуже схожими один на одного (в «звичайному» сенсі), і жоден алгоритм не зможе цього «виправити». Якщо геодезичні відстані можуть бути використані для представлення відмінностей у типах зв'язків (а це концептуальне питання), і якщо актори мають деяку мінливість у своїх відстанях, цей метод може дати значущі результати. Але, на мій погляд, використовувати його слід обережно, якщо взагалі, з неспрямованими даними.

Безперервний REGE для геодезичних відстаней (дані про шлюб Паджетта)

Альтернативний підхід до неспрямованих даних Паджетта полягає у розгляді різних рівнів геодезичних відстаней як мір (оберненої) міцності зв'язків. Кажуть, що два вузли більш еквівалентні, якщо у них є актор подібної відстані по сусідству (подібний в кількісному сенсі «5" більше схожий на «4», ніж «6»). За замовчуванням алгоритм розширює пошук на околиці відстані 3 (хоча можна вибрати менше або більше).

На малюнку 15.8 показані результати застосування Мережа> Ролі та позиції> Максимальний регулярний> Rege до даних Паджетта, використовуючи «3 ітерації» (тобто триступінчасті околиці).

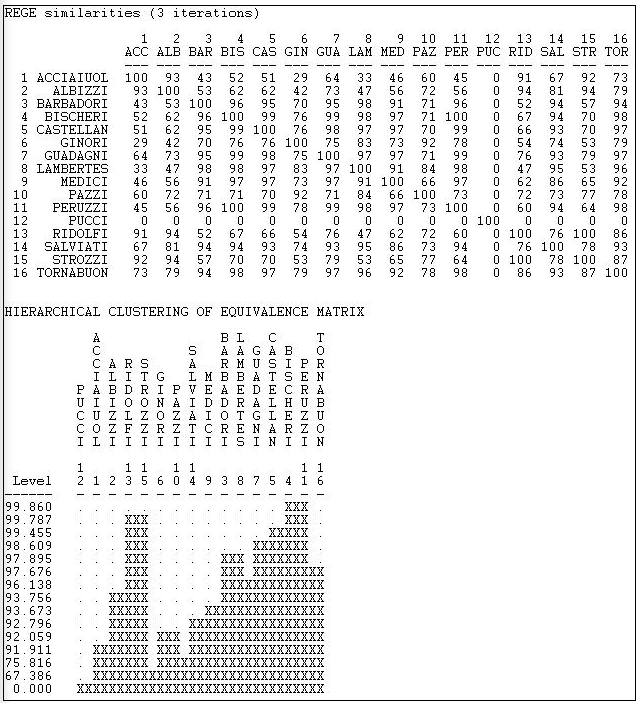
Малюнок 15.8: Безперервний REGE даних шлюбного союзу Паджетта

Перша панель виводу відображає приблизні попарно регулярні подібності у вигляді матриці. Відзначимо, що ізольоване сімейство (Пуччі) трактується як окремий клас. Також відзначимо, що ці результати знаходять досить різні особливості даних, ніж робило категоричне лікування. Безперервний алгоритм REGE, застосований до неспрямованих даних, ймовірно, кращий вибір, ніж категоричний підхід. Результат все ще показує дуже високу регулярну еквівалентність серед акторів, і рішення лише скромно схоже на рішення категоричного підходу.

Мережа обміну інформацією бюрократії Кноке, проаналізована пошуком Табу

Наприкінці нашого аналізу в розділі «Пошук наборів еквівалентності» вище ми створили «перестановлену та заблоковану» версію наших даних. При цьому ми використовували кілька правил, які, по суті, виявляють, як «виглядають» регулярні відносини еквівалентності. Повторити основні моменти: ми не дбаємо про зв'язки між членами регулярного класу; зв'язки між членами регулярного класу та іншого класу або всі нульові, або такі, що кожен член одного класу має прив'язку хоча б до одного члена іншого класу.

Цю «картинку» того, як виглядають звичайні класи, можна використовувати для їх пошуку за допомогою числових методів. Мережа>Ролі та позиції>Максимальний регулярний>Оптимізація алгоритм прагне сортувати вузли в (обрану користувачем кількість) категорій, які наближаються до задоволення «зображення» регулярної еквівалентності, наскільки це можливо. На малюнку 15.9 показані результати застосування цього алгоритму до інформаційної мережі Кноке.

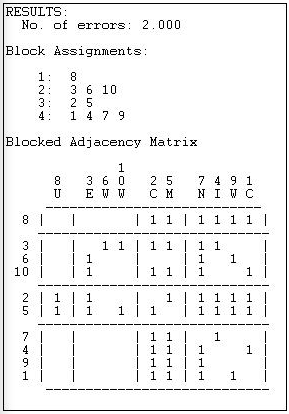
Малюнок 15.9: Чотири регулярні класи еквівалентності для інформаційної мережі Кноке за оптимальним пошуком

Метод створює статистику придатності (кількість помилок), і слід порівнювати рішення для різних чисел розділів.

Однак заблокована матриця суміжності для чотирьох групових рішень є досить переконливою. З 12 цікавить блоку (блоки на діагоналі зазвичай не розглядаються як релевантні для «рольового» аналізу) 11 задовольняють правилам для нуля або одного блоку ідеально. Тільки блок, що з'єднує відправку з {3, 6, 10} до блоку {2, 5}, не задовольняє зображення регулярної еквівалентності (оскільки актор 6 не має зв'язків відправки ні з актором 2, ні 5).

Рішення також цікаве по суті. Наприклад, третій набір {2, 5} - це чисті «повторювачі», які надсилають та отримують від усіх інших ролей. Набір {3, 6, 10} надсилає лише два інших типи (не всі три інші типи) і отримує тільки від одного іншого типу. І так далі.

Метод пошуку табу може бути дуже корисним, і зазвичай дає досить приємні результати. Це ітераційний алгоритм пошуку, однак, і може знаходити локальні рішення. Багато мереж мають більше одного допустимого поділу за регулярною еквівалентністю, і немає ніякої гарантії, що алгоритм завжди знайде одне і те ж рішення. Його слід запускати кілька разів з різними стартовими конфігураціями.