5.1: Аксіоми дійсних чисел

У цьому розділі ми глибоко зануримося в структуру дійсних чисел, створивши безліч властивостей, з якими ви знайомі, починаючи з колекції фундаментальних аксіом. Нагадаємо, що аксіома - це твердження, яке вважається істинним без доказів. Це основні будівельні блоки, з яких доведені всі теореми. Варто зазначити, що з натуральних чисел можна акуратно побудувати дійсні числа. Однак це не буде той підхід, який ми приймаємо. Замість цього ми просто перерахуємо аксіоми, яким задовольняють дійсні числа

Наші аксіоми для дійсних чисел діляться на три категорії:

1. Польові аксіоми: Ці аксіоми забезпечують основні властивості арифметики, що включають додавання та віднімання.
2. Аксіоми порядку: Ці аксіоми забезпечують необхідні властивості нерівностей.
3. Аксіома повноти: Ця аксіома гарантує, що знайома числова лінія, яку ми використовуємо для моделювання дійсних чисел, не має в ній отворів.

Починаємо з польових аксіом.

Аксіоми 5.1. Існують операції\(+\) (додавання) і\(\cdot\) (множення) по\(\mathbb{R}\) задоволенню:

1. (Асоціативність для додавання) Для всього, що\(a, b, c\in \mathbb{R}\) ми маємо\((a+b)+c = a+(b+c)\);
2. (Комутативність для додавання) Для всіх\(a,b\in \mathbb{R}\), у нас є\(a+b=b+a\);
3. (Additive Identity) Існує\(0\in\mathbb{R}\) така, що для всіх\(a\in\mathbb{R}\),\(0+a=a\);
4. (Additive Inverses) Для всього\(a\in\mathbb{R}\) існує\(-a\in\mathbb{R}\) таке, що\(a+(-a)=0\);
5. (Асоціативність для множення) Для всього, що\(a, b, c\in \mathbb{R}\) ми маємо\((ab)c = a(bc)\);
6. (Комутативність для множення) Для всіх\(a,b\in \mathbb{R}\), у нас є\(ab=ba\);
7. (Мультиплікативна ідентичність) Існує\(1\in\mathbb{R}\) така\(a\in\mathbb{R}\), що\(1\neq 0\) і для всіх\(1a=a\);
8. (Мультиплікативні інверси) Для всього\(a\in\mathbb{R}\setminus\{0\}\) існує\(a^{-1}\in\mathbb{R}\) таке, що\(aa^{-1}=1\).
9. (Розподільна власність) Для всіх\(a,b,c\in \mathbb{R}\),\(a(b+c)=ab+ac\);

У мові абстрактної алгебри аксіоми F1—F4 та F5—F8 складають кожну з\(\mathbb{R}\) та\(\mathbb{R}\setminus\{0\}\) абелеву групу при додаванні та множенні відповідно. Axiom F9 забезпечує спосіб взаємодії операцій додавання та множення. У сукупності аксіоми F1—F9 роблять дійсні числа полем. З аксіом випливає, що елементи\(0\) і\(1\) з\(\mathbb{R}\) є унікальними адитивними та мультиплікативними ідентичностями в\(\mathbb{R}\). Щоб довести наступну теорему, припустимо\(0\) і\(0'\) є обидві адитивні ідентичності в,\(\mathbb{R}\) а потім показати, що\(0=0'\). Це показує, що може бути лише одна адитивна ідентичність.

Теорема 5.2. Аддитивна ідентичність\(\mathbb{R}\) унікальна.

Щоб довести наступну теорему, імітуйте підхід, який ви використовували для доведення теореми 5.2.

Теорема 5.3. Мультиплікативна\(\mathbb{R}\) ідентичність унікальна.

Для кожного елементи\(-a\) і\(a^{-1}\) (до тих пір\(a\in\mathbb{R}\), поки\(a\neq 0\)) також є унікальними адитивними і мультиплікативними оберненнями відповідно.

Теорема 5.4. Кожне дійсне число має унікальну добавку, обернену.

Теорема 5.5. Кожне ненульове дійсне число має унікальний мультиплікативний обернений.

Оскільки ми приймаємо формальний аксіоматичний підхід до дійсних чисел, ми повинні дати зрозуміти, як вбудовані натуральні числа\(\mathbb{R}\).

Визначення 5.6. Визначимо натуральні числа, позначаються\(\mathbb{N}\), щоб бути найменшою підмножиною\(\mathbb{R}\) задовольняє:

1. \(1\in\mathbb{N}\), і
2. для всіх\(n\in\mathbb{N}\), у нас є\(n+1\in\mathbb{N}\).

Зверніть увагу на подібність між визначенням натуральних чисел, представлених вище, та аксіомою індукції, наведеним у розділі 4.1. Звичайно, ми використовуємо стандартну систему числення для представлення натуральних чисел, так що\(\mathbb{N}= \{1,2,3,4,5,6,7,8,9,10\ldots\}\).

З огляду на натуральні числа, Аксіома F3/Теорема 5.2 і Аксіома F4/Теорема 5.4 разом з операцією додавання дозволяють визначити цілі числа, позначені\(\mathbb{Z}\), очевидним чином. Тобто цілі числа складаються з натуральних чисел разом з адитивною ідентичністю та всіх адитивних обертань натуральних чисел.

Тепер ми введемо деякі загальні позначення, з якими ви, швидше за все, знайомі. Знайдіть хвилинку, щоб подумати про те, чому наступне - це визначення на відміну від аксіоми чи теореми.

Визначення 5.7. Для кожного\(a,b\in\mathbb{R}\) і\(n\in\mathbb{Z}\) ми визначаємо наступне:

1. \(a-b:= a+(-b)\)
2. \(\displaystyle\frac{a}{b}:= ab^{-1}\)(для\(b\neq 0\))
3. \(\displaystyle a^n:= \begin{cases} \overbrace{aa\cdots a}^n, &\text{if }n\in \mathbb{N}\\ 1, & \text{if }n=0\text{ and }a\neq 0\\ \displaystyle\frac{1}{a^{-n}}, & \text{if }-n\in \mathbb{N}\text{ and }a\neq 0 \end{cases}\)

Набір раціональних чисел, позначений\(\mathbb{Q}\), визначається як сукупність усіх дійсних чисел, що мають форму, наведену в частині (b) Визначення 5.7. Ірраціональні числа визначені бути\(\mathbb{R}\setminus\mathbb{Q}\).

Використовуючи польові аксіоми, ми можемо довести кожне з тверджень у наступній теоремі.

Теорема 5.8. Для всіх\(a,b,c\in\mathbb{R}\) у нас є наступне:

1. \(a=b\)якщо і тільки якщо\(a+c=b+c\);
2. \(0a=0\);
3. \(-a=(-1)a\);
4. \((-1)^2 = 1\);
5. \(-(-a)=a\);
6. Якщо\(a\neq 0\), то\((a^{-1})^{-1}=a\);
7. Якщо\(a\neq 0\) і\(ab = ac\), то\(b = c\).
8. Якщо\(ab=0\), то або\(a=0\) або\(b=0\).

Ретельно доведіть наступну теорему, прямо цитуючи, де ви використовуєте польові аксіоми та теорему 5.8.

Теорема 5.9. Для всіх\(a,b\in\mathbb{R}\), у нас є\((a+b)(a-b)=a^2-b^2\).

Тепер ми введемо аксіоми порядку дійсних чисел.

Аксіоми 5.10. Для\(a,b,c\in \mathbb{R}\), існує відношення\(<\) на\(\mathbb{R}\) задоволення:

1. (Закон трихотомії) Якщо\(a\neq b\), то або\(a<b\) або,\(b<a\) але не обидва;
2. (Транзитивність) Якщо\(a<b\) і\(b<c\), то\(a<c\);
3. Якщо\(a<b\), то\(a+c<b+c\);
4. Якщо\(a<b\) і\(0<c\), то\(ac<bc\);

З огляду на аксіоми 1—4, ми говоримо, що дійсні числа є лінійно впорядкованим полем. Ми називаємо числа більше нуля позитивних і ті, що більше або дорівнює нулю невід'ємним. Існують подібні визначення для негативних і непозитивних.

Зверніть увагу, що аксіоми Ордена формулюються з точки зору «\(<\)». Ми також хотіли б мати можливість використовувати «\(>\)«,\(\leq\) «і «\(\geq\)».

Визначення 5.11. Для\(a,b\in\mathbb{R}\), визначаємо:

1. \(a>b\)якщо\(b<a\);
2. \(a\leq b\)якщо\(a<b\) або\(a=b\);
3. \(a\geq b\)якщо\(b\leq a\).

Зверніть увагу, що ми сприймали існування нерівностей ««\(<\)«, ««,\(>\) «та\(\leq\) «\(\geq\)" на дійсних числах як належне, коли ми визначали інтервали дійсних чисел у визначенні 3.4.

Використовуючи Аксіоми Ордена, ми можемо довести багато знайомих фактів.

Теорема 5.12. Для всіх\(a,b\in\mathbb{R}\), якщо\(a,b>0\), то\(a+b>0\); а якщо\(a,b<0\), то\(a+b<0\).

Наступний результат розширює Axiom 3.

Теорема 5.13. Для всіх\(a,b,c,d\in\mathbb{R}\), якщо\(a<b\) і\(c<d\), то\(a+c<b+d\).

Теорема 5.14. Для всіх\(a\in\mathbb{R}\),\(a>0\) якщо і тільки якщо\(-a<0\).

Теорема 5.15. Якщо\(a\),,\(b\)\(c\), і\(d\) є додатними дійсними числами такі, що\(a<b\) і\(c<d\), то\(ac<bd\).

Теорема 5.16. Для всіх\(a,b\in\mathbb{R}\) у нас є наступне:

1. \(ab>0\)якщо і тільки якщо\(a,b>0\) або\(a,b<0\);
2. \(ab<0\)якщо і тільки якщо\(a<0<b\) або\(b<0<a\).

Теорема 5.17. Для всіх позитивних дійсних чисел\(a\) і\(b\),\(a< b\) якщо і тільки якщо\(a^2< b^2\).

Розглянемо використання трьох випадків при наближенні до доказу наступної теореми.

Теорема 5.18. Для всіх\(a\in\mathbb{R}\), у нас є\(a^2\geq 0\).

Це може стати несподіванкою, що наступний результат вимагає доказів.

Теорема 5.19. У нас є\(0<1\).

Попередня теорема разом з теоремою 5.14 передбачає, що,\(-1<0\) як ви очікуєте. З Axiom O3 також випливає\(n\in\mathbb{Z}\), що для всіх у нас є\(n<n+1\). Ми припускаємо, що між\(n\) і немає цілих чисел\(n+1\).

Теорема 5.20. Для всіх\(a\in\mathbb{R}\), якщо\(a>0\), то\(a^{-1}>0\), і якщо\(a<0\), то\(a^{-1}<0\).

Теорема 5.21. Для всіх\(a,b\in \mathbb{R}\), якщо\(a<b\), то\(-b<-a\).

Останні кілька результатів дозволяють сприймати як належне наше звичайне розуміння того, які дійсні числа є позитивними, а які - негативними. Наступна теорема дає результат, який розширює теорему 5.21.

Теорема 5.22. Для всіх\(a,b,c\in \mathbb{R}\), якщо\(a<b\) і\(c<0\), то\(bc<ac\).

Є спеціальна функція, яку ми тепер можемо ввести.

Визначення 5.23. Дано\(a\in\mathbb{R}\), ми визначаємо абсолютне значення\(a\), позначається\(|a|\), через\[|a|:= \begin{cases} a, & \text{if }a\geq 0\\ -a, & \text{if }a<0. \end{cases}\]

Теорема 5.24. Для всіх\(a\in\mathbb{R}\),\(|a|\geq 0\) при рівності тільки якщо\(a=0\).

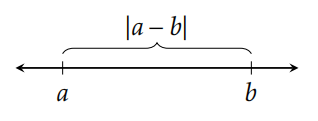
Ми можемо інтерпретувати\(|a|\) як відстань між\(a\) і 0, як зображено на малюнку 5.1.

Малюнок 5.1: Візуальне представлення |a|.

Теорема 5.25. Для всіх\(a,b\in\mathbb{R}\), у нас є\(|a-b|=|b-a|\).

Дано дві точки\(a\) і\(b\)\(|a-b|\), отже, і\(|b-a|\) за попередньою теоремою, відстань між\(a\) і,\(b\) як показано на малюнку 5.2.

Рисунок 5.2: Візуальне представлення |a − b|.

Теорема 5.26. Для всіх\(a,b\in\mathbb{R}\),\(|ab|=|a||b|\).

У наступній теоремі написання\(\pm a\leq b\) - це абревіатура від\(a\leq b\) і\(-a\leq b\).

Теорема 5.27. Для всіх\(a,b\in\mathbb{R}\), якщо\(\pm a\leq b\), то\(|a|\leq b\).

Теорема 5.28. Для всіх\(a\in\mathbb{R}\),\(|a|^2=a^2\).

Теорема 5.29. Для всіх\(a\in\mathbb{R}\),\(\pm a\leq |a|\).

Малюнок 5.3: Візуальне представлення |a| ≤ r.

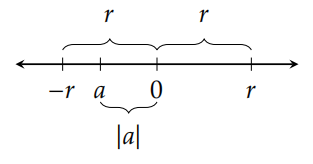
Теорема 5.30. Для всіх\(a,r\in\mathbb{R}\) з\(r\) ненегативними,\(|a|\leq r\) якщо і тільки якщо\(-r\leq a\leq r\).

Буква\(r\) використовувалася в попередній теоремі, оскільки це перша буква слова «радіус». Якщо\(r\) позитивний, ми можемо думати про інтервал\((-r,r)\) як про внутрішню частину одновимірного кола з радіусом по\(r\) центру 0. На малюнку 5.3 представлена наочна інтерпретація теореми 5.30.

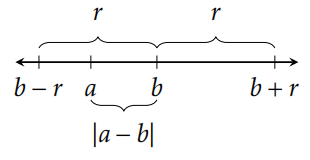
Слідство 5.31. Для всіх\(a,b,r\in\mathbb{R}\) з\(r\) ненегативними,\(|a-b|\leq r\) якщо і тільки якщо\(b-r\leq a\leq b+r\).

Оскільки\(|a-b|\) представляє відстань між\(a\) і\(b\), ми можемо інтерпретувати\(|a-b|\leq r\) як сказати, що відстань між\(a\) і\(b\) менше або дорівнює\(r\). Іншими словами,\(a\) знаходиться в межах\(r\) одиниць\(b\). Див. Рисунок 5.4.

Рисунок 5.4: Візуальне представлення |a − b| ≤ r.

Розглянемо використання теорем 5.29 та 5.30 при атаці наступного результату, який відомий як нерівність трикутника. Цей результат може бути надзвичайно корисним у деяких контекстах.

Теорема 5.32. Для всіх\(a,b\in\mathbb{R}\),\(|a+b|\leq |a|+|b|\).

На малюнку 5.5 зображено два випадки нерівності трикутника.

Малюнок 5.5: Візуальне представлення двох випадків нерівності трикутника

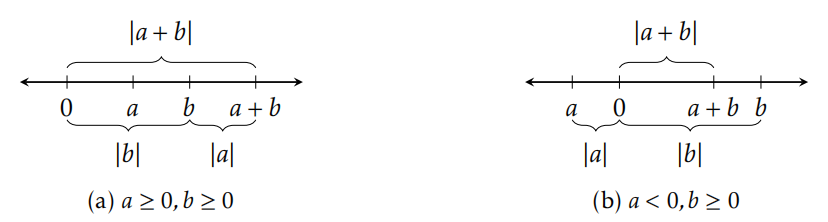
Проблема 5.33. За яких умов ми маємо рівність для нерівності трикутника?

Де трикутник нерівність отримав свою назву? Чому саме «Трикутник»? Для будь-якого трикутника (включаючи вироджені трикутники) сума довжин будь-яких двох сторін повинна бути більше або дорівнює довжині залишилася сторони. Тобто якщо\(x\)\(y\), і\(z\) є довжинами сторін трикутника, то\(z\leq x+y\), де ми маємо рівність тільки в виродженому випадку трикутника без площі. У лінійній алгебрі нерівність трикутника - це теорема про довжини векторів. Якщо\(\mathbf{a}\) і\(\mathbf{b}\) є векторами в\(\mathbb{R}^n\), то нерівність трикутника стверджує, що\(\lVert \mathbf{a}+\mathbf{b}\rVert \leq \lVert\mathbf{a}\rVert +\lVert\mathbf{b}\rVert\). Зверніть увагу, що\(\lVert \mathbf{a}\rVert\) позначає довжину вектора\(\mathbf{a}\). Див. Рисунок 5.6. Версія нерівності трикутника, яку ми представили в теоремі 5.32, є саме одновимірною версією нерівності трикутника через вектори.

Малюнок 5.6: Нерівність трикутника через вектори.

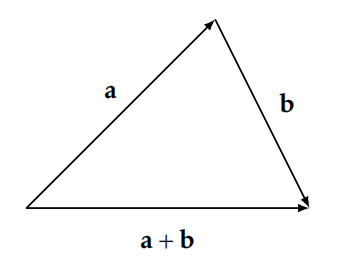
Наступну теорему іноді називають зворотною нерівністю трикутника.

Теорема 5.34. Для всіх\(a,b\in\mathbb{R}\),\(|a-b|\geq \left||a|-|b| \right|\).

Перш ніж ми введемо аксіому повноти, нам потрібна додаткова термінологія.

Визначення 5.35. Нехай\(A\subseteq \mathbb{R}\). Точка\(b\) називається верхньою межею\(A\) if for all\(a\in A\),\(a\leq b\). Кажуть\(A\), що набір обмежений вище, якщо він має верхню межу.

Проблема 5.36. Поняття нижньої межі та властивість множини, що обмежується нижче, визначаються аналогічно. Спробуйте визначити їх.

Проблема 5.37. Знайдіть усі верхні межі та всі нижні межі для кожного з наступних наборів, коли вони існують.

1. \(\{5,11,17,42,103\}\)
2. \(\mathbb{N}\)
3. \(\mathbb{Z}\)
4. \((0,1]\)
5. \((0,1]\cap \mathbb{Q}\)
6. \((0,\infty)\)
7. \(\{42\}\)
8. \(\{\frac{1}{n}\mid n\in\mathbb{N}\}\)
9. \(\{\frac{1}{n}\mid n\in\mathbb{N}\}\cup\{0\}\)
10. \(\emptyset\)

Визначення 5.38. Набір\(A\subseteq \mathbb{R}\) обмежується, якщо він\(A\) обмежений вище і знизу.

Зверніть увагу, що\(A\subseteq\mathbb{R}\) множина обмежена тоді і лише тоді, коли вона є підмножиною деякого обмеженого замкнутого інтервалу.

Визначення 5.39. Нехай\(A\subseteq \mathbb{R}\). Точка\(p\) - це супремум (або найменша верхня межа)\(A\)\(p\) if є верхньою мемою\(A\) і\(p\leq b\) для кожної\(b\) верхньої межі\(A\). Аналогічно, точка\(p\) - це нефімум (або найбільша нижня межа)\(A\) якщо\(p\) є нижньою мемою\(A\) і\(p\geq b\) для кожної\(b\) нижньої межі \(A\).

Наш наступний результат говорить нам, що супремум набору та інфімум набору є унікальними, коли вони існують.

Теорема 5.40. Якщо\(A\subseteq \mathbb{R}\) таке, що супремум (відповідно, infimum) of\(A\) існує, то супремум (відповідно, infimum) з\(A\) є унікальним.

У світлі попередньої теореми, якщо супремум\(A\) існує, він позначається\(\sup(A)\). Аналогічно, якщо інфімум\(A\) існує, він позначається символом\(\inf(A)\).

Проблема 5.41. Знайдіть супремум та інфімум кожного з множин у Задачі 5.37, коли вони існують.

Важливо визнати, що супремум або інфімум набору може міститися, а може і не міститися в наборі. Зокрема, ми маємо наступну теорему щодо супреми та максимумів. Аналогічний результат тримається для інфіми і мінімумів.

Теорема 5.42. Нехай\(A\subseteq \mathbb{R}\). Тоді\(A\) має максимум, якщо і тільки якщо\(A\) має супремум і\(\sup(A)\in A\), в цьому випадку\(\max(A)=\sup(A)\).

Інтуїтивно, точка - це супремум множини\(A\) тоді і тільки тоді, коли жодна точка менша за супремум не може бути верхньою мемою\(A\). Наступний результат робить це більш точним.

Теорема 5.43. Нехай\(A\subseteq \mathbb{R}\) такі,\(A\) що обмежені вище і нехай\(b\) бути верхня межа\(A\). Тоді\(b\) є супремум\(A\) якщо і тільки якщо для кожного\(\varepsilon >0\), існує\(a\in A\) таке, що\(b-\varepsilon <a\).

Проблема 5.44. Створюють та доводять аналогічний результат теоремі 5.43 за участю інфімум.

Наступна аксіома стверджує, що кожна непорожня підмножина дійсних чисел, яка має верхню межу, має найменшу верхню межу.

Аксіоми 5.45. Якщо\(A\) є непорожньою підмножиною\(\mathbb{R}\), яка обмежена вище, то\(\sup(A)\) існує.

З огляду на аксіому повноти, ми говоримо, що дійсні числа задовольняють найменше верхню межу властивості. Варто згадати, що нам не потрібна аксіома повноти, щоб зробити висновок, що кожна непорожня підмножина цілих чисел, яка обмежена вище, має супремум, як це випливає з теореми 4.40 (узагальнена версія принципу Well-Ordering).

Безумовно, дійсні числа також задовольняють аналогічний результат за участю infimum.

Теорема 5.46. Якщо\(A\) є непорожньою підмножиною\(\mathbb{R}\), яка обмежена нижче, то\(\inf(A)\) існує.

Наш наступний результат, який називається Архімедова властивість, говорить нам, що для кожного реального числа ми завжди можемо знайти натуральне число, яке більше. Щоб довести цю теорему, розглянемо доказ протиріччя, а потім використаємо аксіому повноти та теорему 5.43.

Теорема 5.47. Для кожного\(x\in\mathbb{R}\) існує\(n\in\mathbb{N}\) таке, що\(x<n\).

Більш загалом, ми можемо «стиснути» кожне дійсне число між парою цілих чисел. Наступний результат іноді посилається на Узагальнену архімедову властивість.

Теорема 5.48. Для кожного\(x\in\mathbb{R}\) існує\(k,n\in\mathbb{Z}\) таке, що\(k<x<n\).

Теорема 5.49. Для будь-якого позитивного дійсного числа\(x\) існує\(N\in \mathbb{N}\) таке, що\(0<\frac{1}{N}<x\).

Наступна теорема посилює узагальнену властивість архімеда і говорить, що кожне дійсне число є або цілим числом, або лежить між парою послідовних цілих чисел. Щоб довести цю теорему, давайте\(x\in\mathbb{R}\) і визначаємо\(L=\{k\in\mathbb{Z}\mid k\leq x\}\). Використовуйте узагальнену архімедову властивість, щоб зробити висновок, що\(L\) є непорожнім, а потім використайте теорему 4.40.

Теорема 5.50. Для кожного\(x\in\mathbb{R}\) існує\(n\in \mathbb{Z}\) таке, що\(n\leq x<n+1\).

Щоб довести наступну теорему, нехай\(a<b\), використовувати теорему 5.49 на\(b-a\) отримання\(N\in\mathbb{N}\) такого\(\frac{1}{N}<b-a\), що, а потім застосувати теорему 5.50,\(Na\) щоб зробити висновок, що існує\(n\in\mathbb{N}\) таке, що \(n\leq Na<n+1\). Нарешті, стверджуйте, що\(\frac{n+1}{N}\) це раціональне число, яке ви шукаєте.

Теорема 5.51. Якщо\((a,b)\) відкритий інтервал, то існує раціональне число\(p\) таке, що\(p\in(a,b)\).

Нагадаємо, що дійсні числа складаються з раціональних і ірраціональних чисел. Два приклади ірраціонального числа, з яким ви, швидше за все, знайомі, є\(\pi\) і\(\sqrt{2}\). У розділі 6.2 ми доведемо, що\(\sqrt{2}\) це нераціонально, але поки ми будемо приймати цей факт як належне. Виявляється, що\(\sqrt{2}\approx 1.41421356237\in (1,2)\). Це дає приклад ірраціонального числа, що виникає між парою різних раціональних чисел. Наступна теорема є хорошим викликом для узагальнення цього.

Теорема 5.52. Якщо\((a,b)\) відкритий інтервал, то існує ірраціональне число\(p\) таке, що\(p\in(a,b)\).

Повторне застосування попередніх двох теорем передбачає, що кожен відкритий інтервал містить нескінченно багато раціональних чисел і нескінченно багато ірраціональних чисел. У світлі цих двох теорем ми говоримо, що і раціональні, і ірраціональні щільні в дійсних числах.