5.E: Вправи

Вправа\(\PageIndex{1}\)

Показувати карту\(T\):\(\mathbb{R}^n → \mathbb{R}^m\) визначено\(T (\vec{x}) = A\vec{x}\) де\(m\times n\) матриця і\(A\)\(\vec{x}\) є вектором\(m\times 1\) стовпця, є лінійним перетворенням.

Відповідь

Цей результат випливає з властивостей множення матриці.

Вправа\(\PageIndex{2}\)

Показати, що функція,\(T_{\vec{u}}\) визначена, також\(T_{\vec{u}} (\vec{v}) =\vec{v}−proj_{\vec{u}} (\vec{v})\) є лінійним перетворенням.

Відповідь

\[\begin{aligned}T_{\vec{u}}(a\vec{v}+b\vec{w})&=a\vec{v}+b\vec{w}-\frac{(a\vec{v}+b\vec{w}\bullet\vec{u})}{||\vec{u}||^2}\vec{u} \\ &=a\vec{v}-a\frac{(\vec{v}\bullet\vec{u})}{||\vec{u}||^2}\vec{u}+b\vec{w}-b\frac{(\vec{w}\bullet\vec{u})}{||\vec{u}||^2}\vec{u} \\ &=aT_{\vec{u}}(\vec{v})+bT_{\vec{u}}(\vec{w})\end{aligned}\]

Вправа\(\PageIndex{3}\)

\(\vec{u}\)Дозволяти бути фіксованим вектором. Функція,\(T_{\vec{u}}\) визначена за допомогою,\(T_{\vec{u}}\vec{v} =\vec{u}+\vec{v}\) має ефект перекладу всіх векторів шляхом додавання\(\vec{u}\neq\vec{0}\). Покажіть, що це не лінійне перетворення. Поясніть, чому неможливо представити\(T_{\vec{u}}\) в\(\mathbb{R}^3\) множенні на\(3×3\) матрицю.

Відповідь

Лінійні перетворення приймають\(\vec{0}\),\(\vec{0}\)\(T\) до яких ні. Також\(T_{\vec{a}} (\vec{u}+\vec{v})\neq T_{\vec{a}}\vec{u}+T_{\vec{a}}\vec{v}\).

Вправа\(\PageIndex{4}\)

Розглянемо наступні функції, які відображаються\(\mathbb{R}^n\) на\(\mathbb{R}^n\).

1. \(T\)множить\(j\) ту складову\(\vec{x}\) на ненульове число\(b\).
2. \(T\)замінює компонент\(i\) th\(b\) раз на той\(j\) компонент, доданий до компонента.\(\vec{x}\)\(i\)
3. \(T\)перемикає\(i\)\(j\) -й і ті компоненти.

Покажіть ці функції лінійних перетворень і опишіть їх матриці\(A\) такі, що\(T (\vec{x}) = A\vec{x}\).

Відповідь

1. Матриця\(T\) - це елементарна матриця, яка множить\(j\) діагональний запис матриці ідентичності на\(b\).
2. Матриця\(T\) - це елементарна матриця, яка займає\(b\) 3 рази\(j\) від го рядка і додає до\(i\) го рядка.
3. Матриця\(T\) - це елементарна матриця, яка перемикає\(i\) th та\(j\) th рядки, де дві складові знаходяться в\(i\) th та\(j\) th положеннях.

Вправа\(\PageIndex{5}\)

Вам дається лінійне перетворення\(T\):\(\mathbb{R}^n → \mathbb{R}^m\) і ви знаєте, що\[T(A_i)=B_i\nonumber\] де\([A_1\cdots a_n]^{-1}\) існує. Показати, що\(T\) матриця має вигляд\[[B_1\cdots B_n][A_1\cdots A_n]^{-1}\nonumber\]

Відповідь

Припустимо\[\left[\begin{array}{c}\vec{c}_1^{T} \\ \vdots \\ \vec{c}_n^T \end{array}\right]=\left[\begin{array}{ccc}\vec{a}_1&\cdots &\vec{a}_n\end{array}\right]^{-1}\nonumber\], таким чином\(\vec{c}_i^T\vec{a}_j=\delta_{ij}\). Тому\[\begin{aligned} \left[\begin{array}{ccc}\vec{b}_1&\cdots&\vec{b}_n\end{array}\right]\left[\begin{array}{ccc}\vec{a}_1&\cdots&\vec{a}_n\end{array}\right]^{-1}\vec{a}_i&=\left[\begin{array}{ccc}\vec{b}_1&\cdots&\vec{b}_n\end{array}\right]\left[\begin{array}{c}\vec{c}_1^T \\ \vdots \\ \vec{c}_n^T\end{array}\right]\vec{a}_i\\ &=\left[\begin{array}{ccc}\vec{b}_1&\cdots&\vec{b}_n\end{array}\right]\vec{e}_i \\ &=\vec{b}_i\end{aligned}\] Таким чином\(T\vec{a}_i=\left[\begin{array}{ccc}\vec{b}_1&\cdots&\vec{b}_n\end{array}\right]\left[\begin{array}{ccc}\vec{a}_1&\cdots&\vec{a}_n\end{array}\right]^{-1}\vec{a}_i=A\vec{a}_i\). Якщо\(\vec{x}\) довільна, то так як матриця\(\left[\begin{array}{ccc}\vec{a}_1&\cdots&\vec{a}_n\end{array}\right]\) є оборотною, існує унікальна\(\vec{y}\) така, що\(\left[\begin{array}{ccc}\vec{a}_1&\cdots&\vec{a}_n\end{array}\right]\vec{y}=\vec{x}\) Звідси\[T\vec{x}=T\left(\sum\limits_{i=1}^n y_i\vec{a}_i\right)=\sum\limits_{i=1}^n y_iT\vec{a}_i=\sum\limits_{i=1}^n y_iA\vec{a}_i=A\left(\sum\limits_{i=1}^ny_i\vec{a}_i\right)=A\vec{x}\nonumber\]

Вправа\(\PageIndex{6}\)

Припустимо,\(T\) це лінійне перетворення таке, що\[\begin{aligned}T\left[\begin{array}{r}1\\2\\-6\end{array}\right]&=\left[\begin{array}{r}5\\1\\3\end{array}\right] \\ T\left[\begin{array}{r}-1\\-1\\5\end{array}\right]&=\left[\begin{array}{r}1\\1\\5\end{array}\right] \\ T\left[\begin{array}{r}0\\-1\\2\end{array}\right]&=\left[\begin{array}{r}5\\3\\-2\end{array}\right]\end{aligned}\] знайти матрицю\(T\). Тобто знайти\(A\) таке, що\(T(\vec{x}) = A\vec{x}\).

Відповідь

\[\left[\begin{array}{ccc}5&1&5\\1&1&3\\3&5&-2\end{array}\right]\left[\begin{array}{ccc}3&2&1\\2&2&1\\4&1&1\end{array}\right]=\left[\begin{array}{ccc}37&17&11 \\ 17&7&5\\11&14&6\end{array}\right]\nonumber\]

Вправа\(\PageIndex{7}\)

Припустимо,\(T\) це лінійне перетворення таке, що\[\begin{aligned}T\left[\begin{array}{r}1\\1\\-8\end{array}\right]&=\left[\begin{array}{r}1\\3\\1\end{array}\right] \\ T\left[\begin{array}{r}-1\\0\\6\end{array}\right]&=\left[\begin{array}{r}2\\4\\1\end{array}\right] \\ T\left[\begin{array}{r}0\\-1\\3\end{array}\right]&=\left[\begin{array}{r}6\\1\\-1\end{array}\right]\end{aligned}\] знайти матрицю\(T\). Тобто знайти\(A\) таке, що\(T(\vec{x})=A\vec{x}\).

Відповідь

\[\left[\begin{array}{ccc}1&2&6\\3&4&1\\1&1&-1\end{array}\right]\left[\begin{array}{ccc}6&3&1\\5&3&1\\6&2&1\end{array}\right]=\left[\begin{array}{ccc}52&21&9\\44&23&8\\5&4&1\end{array}\right]\nonumber\]

Вправа\(\PageIndex{8}\)

Припустимо,\(T\) це лінійне перетворення таке, що\[\begin{aligned}T\left[\begin{array}{r}1\\3\\-7\end{array}\right]&=\left[\begin{array}{r}-3\\1\\3\end{array}\right] \\ T\left[\begin{array}{r}-1\\-2\\6\end{array}\right]&=\left[\begin{array}{r}1\\3\\-3\end{array}\right] \\ T\left[\begin{array}{r}0\\-1\\2\end{array}\right]&=\left[\begin{array}{r}5\\3\\-3\end{array}\right]\end{aligned}\] знайти матрицю\(T\). Тобто знайти\(A\) таке, що\(T(\vec{x})=A\vec{x}\).

Відповідь

\[\left[\begin{array}{ccc}-3&1&5\\1&3&3\\3&-3&-3\end{array}\right]\left[\begin{array}{ccc}2&2&1\\1&2&1\\4&1&1\end{array}\right]=\left[\begin{array}{ccc}15&1&3\\17&11&7\\-9&-3&-3\end{array}\right]\nonumber\]

Вправа\(\PageIndex{9}\)

Припустимо,\(T\) це лінійне перетворення таке, що\[\begin{aligned}T\left[\begin{array}{r}1\\1\\-7\end{array}\right]&=\left[\begin{array}{r}3\\3\\3\end{array}\right] \\ T\left[\begin{array}{r}-1\\0\\6\end{array}\right]&=\left[\begin{array}{r}1\\2\\3\end{array}\right] \\ T\left[\begin{array}{r}0\\-1\\2\end{array}\right]&=\left[\begin{array}{r}1\\3\\-1\end{array}\right]\end{aligned}\] знайти матрицю\(T\). Тобто знайти\(A\) таке, що\(T(\vec{x})=A\vec{x}\).

Відповідь

\[\left[\begin{array}{ccc}3&1&1\\3&2&3\\3&3&-1\end{array}\right]\left[\begin{array}{ccc}6&2&1\\5&2&1\\6&1&1\end{array}\right]=\left[\begin{array}{ccc}29&9&5\\46&13&8\\27&11&5\end{array}\right]\nonumber\]

Вправа\(\PageIndex{10}\)

Припустимо,\(T\) це лінійне перетворення таке, що\[\begin{aligned}T\left[\begin{array}{r}1\\2\\-18\end{array}\right]&=\left[\begin{array}{r}5\\2\\5\end{array}\right] \\ T\left[\begin{array}{r}-1\\-1\\15\end{array}\right]&=\left[\begin{array}{r}3\\3\\5\end{array}\right] \\ T\left[\begin{array}{r}0\\-1\\4\end{array}\right]&=\left[\begin{array}{r}2\\5\\-2\end{array}\right]\end{aligned}\] знайти матрицю\(T\). Тобто знайти\(A\) таке, що\(T(\vec{x})=A\vec{x}\).

Відповідь

\[\left[\begin{array}{ccc}5&3&2\\2&3&5\\5&5&-2\end{array}\right]\left[\begin{array}{ccc}11&4&1\\10&4&1\\12&3&1\end{array}\right]=\left[\begin{array}{ccc}109&38&10\\112&35&10\\81&34&8\end{array}\right]\nonumber\]

Вправа\(\PageIndex{11}\)

Розглянемо наступні функції\(T : \mathbb{R}^3 → \mathbb{R}^2\). Покажіть, що кожне є лінійним перетворенням і визначте для кожного матрицю\(A\) таку, що\(T(\vec{x}) = A\vec{x}\).

1. \(T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}x+2y+3z \\ 2y-3x+z\end{array}\right]\)
2. \(T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}7x+2y+z \\ 3x-11y+2z\end{array}\right]\)
3. \(T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}3x+2y+z \\ x+2y+6z\end{array}\right]\)
4. \(T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}2y-5x+z \\ x+y+z\end{array}\right]\)

Вправа\(\PageIndex{12}\)

Розглянемо наступні функції\(T : \mathbb{R}^3 → \mathbb{R}^2\). Поясніть, чому кожна з цих функцій не\(T\) є лінійною.

1. \(T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}x+2y+3z+1 \\ 2y-3x+z\end{array}\right]\)
2. \(T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}x+2y^2+3z \\ 2y+3x+z\end{array}\right]\)
3. \(T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}\sin x+2y+3z \\ 2y+3x+z\end{array}\right]\)
4. \(T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}x+2y+3z \\ 2y+3x-\ln z\end{array}\right]\)

Вправа\(\PageIndex{13}\)

Припустимо,\[ [A_1\cdots A_n]^{-1}\nonumber\] існує там, де кожен\(A_j ∈ \mathbb{R}^n\) і нехай вектори\(\{B_1,\cdots ,B_n\}\) в\(\mathbb{R}^m\) бути задані. Показати, що завжди існує лінійне перетворення\(T\) таке, що\(T(A_i) = B_i\).

Вправа\(\PageIndex{14}\)

Знайдіть матрицю для\(T (\vec{w}) = proj_{\vec{v}}(\vec{w})\) де\(\vec{v}=\left[\begin{array}{ccc}1&-2&3\end{array}\right]^T\).

Відповідь

Нагадаємо, що\(proj_{\vec{u}}(\vec{v})=\frac{\vec{v}\bullet\vec{u}}{||\vec{u}||^2}\vec{u}\) і так потрібна матриця має\(i\) стовпець, рівний\(proj_{\vec{u}}(\vec{e}_i)\). Тому бажана матриця є\[\frac{1}{14}\left[\begin{array}{ccc}1&-2&3\\-2&4&-6\\3&-6&9\end{array}\right]\nonumber\]

Вправа\(\PageIndex{15}\)

Знайдіть матрицю для\(T (\vec{w}) = proj_{\vec{v}}(\vec{w})\) де\(\vec{v}=\left[\begin{array}{ccc}1&5&3\end{array}\right]^T\).

Відповідь

\[\frac{1}{35}\left[\begin{array}{ccc}1&5&3\\5&25&15\\3&15&9\end{array}\right]\nonumber\]

Вправа\(\PageIndex{16}\)

Знайдіть матрицю для\(T (\vec{w}) = proj_{\vec{v}}(\vec{w})\) де\(\vec{v}=\left[\begin{array}{ccc}1&0&3\end{array}\right]^T\).

Відповідь

\[\frac{1}{10}\left[\begin{array}{ccc}1&0&3\\0&0&0\\3&0&9\end{array}\right]\nonumber\]

Вправа\(\PageIndex{17}\)

Показати, що якщо функція\(T :\mathbb{R}^n → \mathbb{R}^m\) лінійна, то це завжди так\(T(\vec{0})=\vec{0}\).

Вправа\(\PageIndex{18}\)

\(T\)Дозволяти лінійне перетворення, індуковане матрицею,\(A=\left[\begin{array}{cc}3&1\\-1&2\end{array}\right]\) і\(S\) лінійне перетворення, індуковане\(B=\left[\begin{array}{cc}0&-2\\4&2\end{array}\right]\). Знайти матрицю\(S\circ T\) і знайти\((S\circ T)(\vec{x})\) для\(\vec{x}=\left[\begin{array}{r}2\\-1\end{array}\right]\).

Відповідь

Матриця\(S\circ T\) задається за допомогою\(BA\). \[\left[\begin{array}{cc}0&-2\\4&2\end{array}\right]\left[\begin{array}{cc}3&1\\-1&2\end{array}\right]=\left[\begin{array}{cc}2&-4\\10&8\end{array}\right]\nonumber\]Тепер,\((S\circ T)(\vec{x})=(BA)\vec{x}\). \[\left[\begin{array}{cc}2&-4\\10&8\end{array}\right]\left[\begin{array}{c}2\\-1\end{array}\right]=\left[\begin{array}{c}8\\12\end{array}\right]\nonumber\]

Вправа\(\PageIndex{19}\)

\(T\)Дозволяти лінійне перетворення і припустимо\(T\left(\left[\begin{array}{r}1\\-4\end{array}\right]\right)=\left[\begin{array}{r}2\\-3\end{array}\right]\). Припустимо,\(S\) це лінійне перетворення, індуковане матрицею\(B=\left[\begin{array}{cc}1&2\\-1&3\end{array}\right]\). Знайти\((S\circ T)(\vec{x})\) для\(\vec{x}=\left[\begin{array}{r}1\\-4\end{array}\right]\).

Відповідь

Щоб знайти,\((S\circ T)(\vec{x})\) обчислюємо\(S(T(\vec{x}))\). \[\left[\begin{array}{cc}1&2\\-1&3\end{array}\right]\left[\begin{array}{c}2\\-3\end{array}\right]=\left[\begin{array}{c}-4\\-11\end{array}\right]\nonumber\]

Вправа\(\PageIndex{20}\)

\(T\)Дозволяти лінійне перетворення, індуковане матрицею\(S\),\(A=\left[\begin{array}{cc}2&3\\1&1\end{array}\right]\) і лінійне перетворення, індуковане\(B=\left[\begin{array}{cc}-1&3\\1&-2\end{array}\right]\). Знайти матрицю\(S\circ T\) і знайти\((S\circ T)(\vec{x})\) для\(\vec{x}=\left[\begin{array}{c}5\\6\end{array}\right]\).

Вправа\(\PageIndex{21}\)

\(T\)Дозволяти лінійне перетворення, індуковане матрицею\(A=\left[\begin{array}{cc}2&1\\5&2\end{array}\right]\). Знайдіть матрицю\(T^{-1}\).

Відповідь

Матриця\(T^{-1}\) є\(A^{-1}\). \[\left[\begin{array}{cc}2&1\\5&2\end{array}\right]^{-1}=\left[\begin{array}{cc}-2&1\\5&-2\end{array}\right]\nonumber\]

Вправа\(\PageIndex{22}\)

\(T\)Дозволяти лінійне перетворення, індуковане матрицею\(A=\left[\begin{array}{cc}4&-3\\2&-2\end{array}\right]\). Знайдіть матрицю\(T^{-1}\).

Вправа\(\PageIndex{23}\)

\(T\)Дозволяти лінійне перетворення і припустимо\(T\left(\left[\begin{array}{c}1\\2\end{array}\right]\right)=\left[\begin{array}{c}9\\8\end{array}\right],\:T\left(\left[\begin{array}{r}0\\-1\end{array}\right]\right)=\left[\begin{array}{c}-4\\-3\end{array}\right]\). Знайдіть матрицю\(T^{-1}\).

Вправа\(\PageIndex{24}\)

Знайдіть матрицю для лінійного перетворення, яка обертає кожен вектор на кут\(π/3\).\(\mathbb{R}^2\)

Відповідь

\(\left[\begin{array}{cc}\cos\left(\frac{\pi}{3}\right)&-\sin\left(\frac{\pi}{3}\right) \\ \sin\left(\frac{\pi}{3}\right)&\cos\left(\frac{\pi}{3}\right)\end{array}\right]=\left[\begin{array}{cc}\frac{1}{2}&-\frac{1}{2}\sqrt{3} \\ \frac{1}{2}\sqrt{3}&\frac{1}{2}\end{array}\right]\)

Вправа\(\PageIndex{25}\)

Знайдіть матрицю для лінійного перетворення, яка обертає кожен вектор на кут\(π/4\).\(\mathbb{R}^2\)

Відповідь

\(\left[\begin{array}{cc}\cos\left(\frac{\pi}{4}\right)&-\sin\left(\frac{\pi}{4}\right) \\ \sin\left(\frac{\pi}{4}\right)&\cos\left(\frac{\pi}{4}\right)\end{array}\right]=\left[\begin{array}{cc}\frac{1}{2}\sqrt{2}&-\frac{1}{2}\sqrt{2} \\ \frac{1}{2}\sqrt{2}&\frac{1}{2}\sqrt{2}\end{array}\right]\)

Вправа\(\PageIndex{26}\)

Знайдіть матрицю для лінійного перетворення, яка обертає кожен вектор на кут\(-π/3\).\(\mathbb{R}^2\)

Відповідь

\(\left[\begin{array}{cc}\cos\left(-\frac{\pi}{3}\right)&-\sin\left(-\frac{\pi}{3}\right) \\ \sin\left(-\frac{\pi}{3}\right)&\cos\left(-\frac{\pi}{3}\right)\end{array}\right]=\left[\begin{array}{cc}\frac{1}{2}&\frac{1}{2}\sqrt{3} \\ -\frac{1}{2}\sqrt{3}&\frac{1}{2}\end{array}\right]\)

Вправа\(\PageIndex{27}\)

Знайдіть матрицю для лінійного перетворення, яка обертає кожен вектор на кут\(2π/3\).\(\mathbb{R}^2\)

Відповідь

\(\left[\begin{array}{cc}\cos\left(\frac{2\pi}{3}\right)&-\sin\left(\frac{2\pi}{3}\right) \\ \sin\left(\frac{2\pi}{3}\right)&\cos\left(\frac{2\pi}{3}\right)\end{array}\right]=\left[\begin{array}{cc}-\frac{1}{2}&-\frac{1}{2}\sqrt{3} \\ \frac{1}{2}\sqrt{3}&-\frac{1}{2}\end{array}\right]\)

Вправа\(\PageIndex{28}\)

Знайдіть матрицю для лінійного перетворення, яка обертає кожен вектор на кут\(π/12\).\(\mathbb{R}^2\) Підказка: Зауважте, що\(\pi /12=\pi /3-\pi /4\).

Відповідь

\[\begin{aligned}&\left[\begin{array}{cc}\cos\left(\frac{\pi}{3}\right)&-\sin\left(\frac{\pi}{3}\right) \\ \sin\left(\frac{\pi}{3}\right)&\cos\left(\frac{\pi}{3}\right)\end{array}\right]\left[\begin{array}{cc}\cos\left(-\frac{\pi}{4}\right)&-\sin\left(-\frac{\pi}{4}\right) \\ \sin\left(-\frac{\pi}{4}\right)&\cos\left(-\frac{\pi}{4}\right)\end{array}\right] \\ =&\left[\begin{array}{cc}\frac{1}{4}\sqrt{2}\sqrt{3}+\frac{1}{4}\sqrt{2}&\frac{1}{4}\sqrt{2}-\frac{1}{4}\sqrt{2}\sqrt{3} \\ \frac{1}{4}\sqrt{2}\sqrt{3}-\frac{1}{4}\sqrt{2}&\frac{1}{4}\sqrt{2}\sqrt{3}+\frac{1}{4}\sqrt{2}\end{array}\right]\end{aligned}\]

Вправа\(\PageIndex{29}\)

Знайдіть матрицю для лінійного перетворення, яка обертає кожен вектор\(\mathbb{R}^2\) на кут,\(2π/3\) а потім відображає поперек\(x\) осі.

Відповідь

\[\left[\begin{array}{cc}1&0\\0&-1\end{array}\right]\left[\begin{array}{cc}\cos\left(\frac{2\pi}{3}\right)&-\sin\left(\frac{2\pi}{3}\right) \\ \sin\left(\frac{2\pi}{3}\right)&\cos\left(\frac{2\pi}{3}\right)\end{array}\right]=\left[\begin{array}{cc}-\frac{1}{2}&-\frac{1}{2}\sqrt{3}\\-\frac{1}{2}\sqrt{3}&\frac{1}{2}\end{array}\right]\nonumber\]

Вправа\(\PageIndex{30}\)

Знайдіть матрицю для лінійного перетворення, яка обертає кожен вектор\(\mathbb{R}^2\) на кут,\(π/3\) а потім відображає поперек\(x\) осі.

Відповідь

\[\left[\begin{array}{cc}1&0\\0&-1\end{array}\right]\left[\begin{array}{cc}\cos\left(\frac{\pi}{3}\right)&-\sin\left(\frac{\pi}{3}\right) \\ \sin\left(\frac{\pi}{3}\right)&\cos\left(\frac{\pi}{3}\right)\end{array}\right]=\left[\begin{array}{cc}\frac{1}{2}&-\frac{1}{2}\sqrt{3}\\-\frac{1}{2}\sqrt{3}&-\frac{1}{2}\end{array}\right]\nonumber\]

Вправа\(\PageIndex{31}\)

Знайдіть матрицю для лінійного перетворення, яка обертає кожен вектор\(\mathbb{R}^2\) на кут,\(π/4\) а потім відображає поперек\(x\) осі.

Відповідь

\[\left[\begin{array}{cc}1&0\\0&-1\end{array}\right]\left[\begin{array}{cc}\cos\left(\frac{\pi}{4}\right)&-\sin\left(\frac{\pi}{4}\right) \\ \sin\left(\frac{\pi}{4}\right)&\cos\left(\frac{\pi}{4}\right)\end{array}\right]=\left[\begin{array}{cc}\frac{1}{2}\sqrt{2}&-\frac{1}{2}\sqrt{2}\\-\frac{1}{2}\sqrt{2}&-\frac{1}{2}\sqrt{2}\end{array}\right]\nonumber\]

Вправа\(\PageIndex{32}\)

Знайдіть матрицю для лінійного перетворення, яка обертає кожен вектор на кут,\(π/6\) а потім відображає поперек\(x\) осі з подальшим відображенням по\(y\) осі.\(\mathbb{R}^2\)

Відповідь

\[\left[\begin{array}{cc}-1&0\\0&1\end{array}\right]\left[\begin{array}{cc}\cos\left(\frac{\pi}{6}\right)&-\sin\left(\frac{\pi}{6}\right) \\ \sin\left(\frac{\pi}{6}\right)&\cos\left(\frac{\pi}{6}\right)\end{array}\right]=\left[\begin{array}{cc}-\frac{1}{2}\sqrt{3}&\frac{1}{2}\\ \frac{1}{2}&\frac{1}{2}\sqrt{3}\end{array}\right]\nonumber\]

Вправа\(\PageIndex{33}\)

Знайдіть матрицю для лінійного перетворення, яка обертає кожен вектор\(\mathbb{R}^2\) поперек\(x\) осі, а потім обертає кожен вектор на кут\(\pi /4\).

Відповідь

\[\left[\begin{array}{cc}\cos\left(\frac{\pi}{4}\right)&-\sin\left(\frac{\pi}{4}\right) \\ \sin\left(\frac{\pi}{4}\right)&\cos\left(\frac{\pi}{4}\right)\end{array}\right]\left[\begin{array}{cc}1&0\\0&-1\end{array}\right]=\left[\begin{array}{cc}\frac{1}{2}\sqrt{2}&\frac{1}{2}\sqrt{2} \\ \frac{1}{2}\sqrt{2}&-\frac{1}{2}\sqrt{2}\end{array}\right]\nonumber\]

Вправа\(\PageIndex{34}\)

Знайдіть матрицю для лінійного перетворення, яка обертає кожен вектор\(\mathbb{R}^2\) поперек\(y\) осі, а потім обертає кожен вектор на кут\(\pi /4\).

Відповідь

\[\left[\begin{array}{cc}\cos\left(\frac{\pi}{4}\right)&-\sin\left(\frac{\pi}{4}\right) \\ \sin\left(\frac{\pi}{4}\right)&\cos\left(\frac{\pi}{4}\right)\end{array}\right]\left[\begin{array}{cc}-1&0\\0&1\end{array}\right]=\left[\begin{array}{cc}-\frac{1}{2}\sqrt{2}&-\frac{1}{2}\sqrt{2} \\ -\frac{1}{2}\sqrt{2}&\frac{1}{2}\sqrt{2}\end{array}\right]\nonumber\]

Вправа\(\PageIndex{35}\)

Знайдіть матрицю для лінійного перетворення, яка обертає кожен вектор\(\mathbb{R}^2\) поперек\(x\) осі, а потім обертає кожен вектор на кут\(\pi /6\).

Відповідь

\[\left[\begin{array}{cc}\cos\left(\frac{\pi}{6}\right)&-\sin\left(\frac{\pi}{6}\right) \\ \sin\left(\frac{\pi}{6}\right)&\cos\left(\frac{\pi}{6}\right)\end{array}\right]\left[\begin{array}{cc}1&0\\0&-1\end{array}\right]=\left[\begin{array}{cc}\frac{1}{2}\sqrt{3}&\frac{1}{2} \\ \frac{1}{2}&-\frac{1}{2}\sqrt{3}\end{array}\right]\nonumber\]

Вправа\(\PageIndex{36}\)

Знайдіть матрицю для лінійного перетворення, яка обертає кожен вектор\(\mathbb{R}^2\) поперек\(y\) осі, а потім обертає кожен вектор на кут\(\pi /6\).

Відповідь

\[\left[\begin{array}{cc}\cos\left(\frac{\pi}{6}\right)&-\sin\left(\frac{\pi}{6}\right) \\ \sin\left(\frac{\pi}{6}\right)&\cos\left(\frac{\pi}{6}\right)\end{array}\right]\left[\begin{array}{cc}-1&0\\0&1\end{array}\right]=\left[\begin{array}{cc}-\frac{1}{2}\sqrt{3}&-\frac{1}{2} \\ -\frac{1}{2}&\frac{1}{2}\sqrt{3}\end{array}\right]\nonumber\]

Вправа\(\PageIndex{37}\)

Знайдіть матрицю для лінійного перетворення, яка обертає кожен вектор на кут\(5\pi /12\).\(\mathbb{R}^2\) Підказка: Зауважте, що\(5\pi /12=2\pi /3-\pi /4\).

Відповідь

\[\left[\begin{array}{cc}\cos\left(\frac{2\pi}{3}\right)&-\sin\left(\frac{2\pi}{3}\right) \\ \sin\left(\frac{2\pi}{3}\right)&\cos\left(\frac{2\pi}{3}\right)\end{array}\right]\left[\begin{array}{cc}\cos\left(-\frac{\pi}{4}\right)&-\sin\left(-\frac{\pi}{4}\right) \\ \sin\left(-\frac{\pi}{4}\right)&\cos\left(-\frac{\pi}{4}\right)\end{array}\right]=\nonumber\]\[\left[\begin{array}{cc}\frac{1}{4}\sqrt{2}\sqrt{3}-\frac{1}{4}\sqrt{2}&-\frac{1}{4}\sqrt{2}\sqrt{3}-\frac{1}{4}\sqrt{2} \\ \frac{1}{4}\sqrt{2}\sqrt{3}+\frac{1}{4}\sqrt{2}&\frac{1}{4}\sqrt{2}\sqrt{3}-\frac{1}{4}\sqrt{2}\end{array}\right]\nonumber\]Зверніть увагу, що про порядок в даному випадку не має значення.

Вправа\(\PageIndex{38}\)

Знайдіть матрицю лінійного перетворення, яка обертає кожен вектор проти\(\mathbb{R}^3\) годинникової стрілки навколо\(z\) осі, якщо дивитися з позитивної\(z\) осі на кут,\(30^◦\) а потім відбивається через\(xy\) площину.

Відповідь

\[\left[\begin{array}{ccc}1&0&0\\0&1&0\\0&0&-1\end{array}\right]\left[\begin{array}{ccc}\cos\left(\frac{\pi}{6}\right)&-\sin\left(\frac{\pi}{6}\right)&0 \\ \sin\left(\frac{\pi}{6}\right)&\cos\left(\frac{\pi}{6}\right)&0 \\ 0&0&1\end{array}\right]=\left[\begin{array}{ccc}\frac{1}{2}\sqrt{3}&-\frac{1}{2}&0\\ \frac{1}{2}&\frac{1}{2}\sqrt{3}&0\\0&0&-1\end{array}\right]\nonumber\]

Вправа\(\PageIndex{39}\)

\(\vec{u}=\left[\begin{array}{c}a\\b\end{array}\right]\)Дозволяти бути одиничний вектор в\(\mathbb{R}^2\). Знайдіть матрицю, яка відображає всі вектори в цьому векторі, як показано на наступному малюнку.

Малюнок\(\PageIndex{1}\)

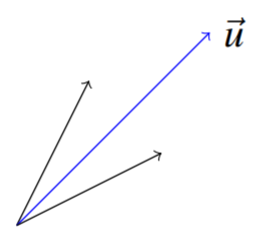
Підказка: Зверніть увагу, що\(\left[\begin{array}{c}a\\b\end{array}\right]=\left[\begin{array}{c}\cos\theta \\ \sin\theta\end{array}\right]\) для деяких\(\theta\). Спочатку обертаємо наскрізь\(-\theta\). Далі відбиваємо через\(x\) вісь. Нарешті обертаємо наскрізь\(\theta\).

Відповідь

\[\begin{aligned} &\left[\begin{array}{cc}\cos (\theta )&-\sin(\theta) \\ \sin(\theta)&\cos(\theta)\end{array}\right]\left[\begin{array}{cc}1&0\\0&-1\end{array}\right]\left[\begin{array}{cc}\cos(-\theta)&-\sin(\theta) \\ \sin(-\theta)&\cos(-\theta)\end{array}\right] \\ =&\left[\begin{array}{cc}\cos^2\theta-\sin^2\theta &2\cos\theta\sin\theta \\ 2\cos\theta\sin\theta&\sin^2\theta-\cos^2\theta\end{array}\right]\end{aligned}\]Тепер писати з точки зору\((a,b)\), зверніть увагу на те\(a/\sqrt{a^2+b^2}=\cos\theta\), що,\(b/\sqrt{a^2+b^2}=\sin\theta\). Тепер підключіть це до вищезазначеного. Результат -\[\left[\begin{array}{cc}\frac{a^2-b^2}{a^2+b^2}&2\frac{ab}{a^2+b^2} \\ 2\frac{ab}{a^2+b^2}&\frac{b^2-a^2}{a^2+b^2}\end{array}\right]=\frac{1}{a^2+b^2}\left[\begin{array}{cc}a^2-b^2&2ab \\ 2ab&b^2-a^2\end{array}\right]\nonumber\] Так як це одиничний вектор,\(a^2+b^2=1\) і таким чином ви отримаєте\[\left[\begin{array}{cc}a^2-b^2&2ab \\ 2ab&b^2-a^2\end{array}\right]\nonumber\]

Вправа\(\PageIndex{40}\)

\(T\)Дозволяти лінійне перетворення, задане\[T\left[\begin{array}{c}x\\y\end{array}\right]=\left[\begin{array}{cc}2&1\\0&1\end{array}\right]\left[\begin{array}{c}x\\y\end{array}\right]\nonumber\] є\(T\) один до одного? Є\(T\) на?

Вправа\(\PageIndex{41}\)

\(T\)Дозволяти лінійне перетворення, задане\[T\left[\begin{array}{c}x\\y\end{array}\right]=\left[\begin{array}{cc}-1&2\\2&1\\1&4\end{array}\right]\left[\begin{array}{c}x\\y\end{array}\right]\nonumber\] є\(T\) один до одного? Є\(T\) на?

Вправа\(\PageIndex{42}\)

\(T\)Дозволяти лінійне перетворення, задане\[T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{ccc}2&0&1\\1&2&-1\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]\nonumber\] є\(T\) один до одного? Є\(T\) на?

Вправа\(\PageIndex{43}\)

\(T\)Дозволяти лінійне перетворення, задане\[T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{ccc}1&3&-5\\2&0&2\\2&4&-6\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]\nonumber\] є\(T\) один до одного? Є\(T\) на?

Вправа\(\PageIndex{44}\)

Наведіть приклад\(3\times 2\) матриці з властивістю, що лінійне перетворення, визначене цією матрицею, є один до одного, але не на.

Відповідь

\[\left[\begin{array}{cc}1&0\\0&1\\0&0\end{array}\right]\nonumber\]

Вправа\(\PageIndex{45}\)

Припустимо,\(A\) це\(m\times n\) матриця, в якій\(m ≤ n\). Припустимо також, що ранг\(A\) дорівнює\(m\). Покажіть, що перетворення\(T\) визначається\(A\) картами\(\mathbb{R}^n\) на\(\mathbb{R}^m\). Підказка: Вектори\(\vec{e}_1,\cdots ,\vec{e}_m\) зустрічаються у вигляді стовпців у зменшеній формі рядка-ешелону для\(A\).

Відповідь

Це говорить про те, що стовпці\(A\) мають підмножину\(m\) векторів, які лінійно незалежні. Тому цей набір векторів є основою для\(\mathbb{R}^m\). Звідси випливає, що проліт колон весь з\(\mathbb{R}^m\). Таким\(A\) чином, на.

Вправа\(\PageIndex{46}\)

Припустимо,\(A\) це\(m\times n\) матриця, в якій\(m ≥ n\). Припустимо також, що ранг\(A\) дорівнює\(n\). Покажіть,\(A\) що один до одного. Підказка: Якщо ні, існує вектор,\(\vec{x}\) такий\(A\vec{x} = 0\), що, і це означає, що принаймні один стовпець\(A\) є лінійною комбінацією інших. Показати це вимагатиме, щоб ранг був меншим, ніж\(n\).

Відповідь

Колони незалежні. Тому\(A\) один до одного.

Вправа\(\PageIndex{47}\)

Поясніть, чому\(n\times n\) матриця\(A\) є як один до одного, так і на, якщо і тільки якщо її ранг\(n\).

Відповідь

Ранг -\(n\) це те саме, що говорити, що стовпці є незалежними, що те саме, що говорити\(A\) один до одного, що те саме, що говорити стовпці є основою. Таким чином, проліт колон\(A\) є все\(\mathbb{R}^n\) і так\(A\) знаходиться на. Якщо\(A\) на, то стовпці повинні бути лінійно незалежними, оскільки в іншому випадку проліт цих стовпців буде мати розмір менше, ніж\(n\) і тому розмір\(\mathbb{R}^n\) буде менше\(n\).

Вправа\(\PageIndex{48}\)

\(W\)Дозволяти\(V\) і бути\(\mathbb{R}^n\) підпростори і\(\mathbb{R}^m\) відповідно і нехай\(T : V → W\) бути лінійним перетворенням. Припустимо,\(\{T\vec{v}_1,\cdots ,T\vec{v}_r\}\) що лінійно незалежний. Покажіть, що це повинен бути випадок, який також\(\{T\vec{v}_1,\cdots ,T\vec{v}_r\}\) є лінійно незалежним.

Відповідь

Якщо\(\sum_i^r a_i\vec{v}_r=0\), то використовуючи властивості лінійності\(T\) ми отримуємо\[0=T(0)=T\left(\sum\limits_i^ra_i\vec{v}_r\right)=\sum\limits_i^ra_iT(\vec{v}_r).\nonumber\] Так як ми припускаємо, що\(\{T\vec{v}_a,\cdots ,T\vec{v}_r\}\) є лінійно незалежним, ми повинні мати все\(a_i = 0\), і тому робимо висновок,\(\{\vec{v}_1,\cdots ,\vec{v}_r\}\) що також лінійно незалежний.

Вправа\(\PageIndex{49}\)

Нехай\[V=span\left\{\left[\begin{array}{c}1\\1\\2\\0\end{array}\right],\:\left[\begin{array}{c}0\\1\\1\\1\end{array}\right],\:\left[\begin{array}{c}1\\1\\0\\1\end{array}\right]\right\}\nonumber\] нехай\(T\vec{x}=A\vec{x}\) де\(A\) є матриця\[\left[\begin{array}{cccc}1&1&1&1\\0&1&1&0\\0&1&2&1\\1&1&1&2\end{array}\right]\nonumber\] Дайте основу для\(im(T)\).

Вправа\(\PageIndex{50}\)

\[V=span\left\{\left[\begin{array}{c}1\\0\\0\\1\end{array}\right],\:\left[\begin{array}{c}1\\1\\1\\1\end{array}\right],\:\left[\begin{array}{c}1\\4\\4\\1\end{array}\right]\right\}\nonumber\]Нехай\(T\vec{x}=A\vec{x}\) де\(A\) є матриця\[\left[\begin{array}{cccc}1&1&1&1\\0&1&1&0\\0&1&2&1\\1&1&1&2\end{array}\right]\nonumber\] Знайти основу для\(im(T)\). При цьому вихідні вектори не утворюють самостійного множини.

Відповідь

Так як третій вектор - це лінійні комбінації перших двох, то зображення третього вектора також буде лінійними комбінаціями зображення перших двох. Однак зображення перших двох векторів лінійно незалежні (перевірте!) , А значить, формують основу образу.

Таким чином, основою для\(im(T)\) є:\[V=span\left\{\left[\begin{array}{c}2\\0\\1\\3\end{array}\right],\:\left[\begin{array}{c}4\\2\\4\\5\end{array}\right]\right\}\nonumber\]

Вправа\(\PageIndex{51}\)

Якщо\(\{\vec{v}_1,\cdots ,\vec{v}_r\}\) лінійно незалежний і\(T\) є лінійним перетворенням один до одного, показати,\(\{T\vec{v}_1,\cdots ,T\vec{v}_r\}\) що також лінійно незалежний. Наведіть приклад, який показує, що якщо\(T\) є лише лінійним, може статися, що, хоча і\(\{\vec{v}_1,\cdots ,\vec{v}_r\}\) є лінійно незалежним, не\(\{T\vec{v}_1,\cdots ,T\vec{v}_r\}\) є. Насправді, показати, що може статися, що кожен з\(T\vec{v}_j\) дорівнює\(0\).

Вправа\(\PageIndex{52}\)

\(W\)Дозволяти\(V\) і бути\(\mathbb{R}^n\) підпростори і\(\mathbb{R}^m\) відповідно і нехай\(T : V → W\) бути лінійним перетворенням. Показати, що якщо\(T\) є на\(W\) і якщо\(\{\vec{v}_1,\cdots ,\vec{v}_r\}\) є основою для\(V\), то\(span\{T\vec{v}_1,\cdots ,T\vec{v}_r\} = W\).

Вправа\(\PageIndex{53}\)

Визначте\(T\):\(\mathbb{R}^4\to\mathbb{R}^3\) наступним чином. \[T\vec{x}=\left[\begin{array}{cccc}3&2&1&8\\2&2&-2&6\\1&1&-1&3\end{array}\right]\vec{x}\nonumber\]Знайдіть основу для\(im(T)\). Також знайдіть основу для\(\text{ker}(T)\).

Вправа\(\PageIndex{54}\)

Визначте\(T\):\(\mathbb{R}^3\to\mathbb{R}^3\) наступним чином. \[T\vec{x}=\left[\begin{array}{ccc}1&2&0\\1&1&1\\0&1&1\end{array}\right]\vec{x}\nonumber\]де праворуч, це просто матричне множення вектора,\(\vec{x}\) який мається на увазі. Поясніть, чому\(T\) є ізоморфізм\(\mathbb{R}^3\) до\(\mathbb{R}^3\).

Вправа\(\PageIndex{55}\)

Припустимо\(T\):\(\mathbb{R}^3\to\mathbb{R}^3\) це лінійне перетворення,\(A\) задане\[T\vec{x}=A\vec{x}\nonumber\] де\(3\times 3\) матриця. Покажіть, що\(T\) є ізоморфізмом тоді і тільки тоді, коли\(A\) є оборотним.

Вправа\(\PageIndex{56}\)

Припустимо\(T\):\(\mathbb{R}^n\to\mathbb{R}^m\) це лінійне перетворення,\(A\) задане\[T\vec{x}=A\vec{x}\nonumber\] де\(m\times n\) матриця. Покажіть,\(T\) що ніколи не є ісморфізмом, якщо\(m\neq n\). Зокрема, показати, що якщо\(m>n\),\(T\) не може бути на і якщо\(m<n\), то\(T\) не може бути один до одного.

Вправа\(\PageIndex{57}\)

Визначте\(T\):\(\mathbb{R}^2\to\mathbb{R}^3\) наступним чином. \[T\vec{x}=\left[\begin{array}{cc}1&0\\1&1\\0&1\end{array}\right]\vec{x}\nonumber\]де праворуч, це просто матричне множення вектора,\(\vec{x}\) який мається на увазі. Покажіть,\(T\) що один до одного. Далі нехай\(W = im(T)\). Показати, що\(T\) є ізоморфізмом\(\mathbb{R}^2\) і\(im (T)\).

Вправа\(\PageIndex{58}\)

У наведеній вище задачі знайдіть\(2\times 3\) матрицю\(A\) таку, що обмеження\(A\) to\(im(T)\) дає той же результат, що і\(T^{−1}\) на\(im(T)\). Підказка: Ви можете дозволити\(A\) бути таким, що\[A\left[\begin{array}{c}1\\1\\0\end{array}\right]=\left[\begin{array}{c}1\\0\end{array}\right],\:A\left[\begin{array}{c}0\\1\\1\end{array}\right]=\left[\begin{array}{c}0\\1\end{array}\right]\nonumber\] тепер знайти інший вектор,\(\vec{v}\in\mathbb{R}^3\) такий, який\[\left\{\left[\begin{array}{c}1\\1\\0\end{array}\right],\:\left[\begin{array}{c}0\\1\\1\end{array}\right],\:\vec{v}\right\}\nonumber\] є основою. Ви можете вибрати,\[\vec{v}=\left[\begin{array}{c}0\\0\\1\end{array}\right]\nonumber\] наприклад. Поясніть, чому це працює або один на ваш вибір працює. Тоді ви можете визначити,\(A\vec{v}\) щоб дорівнювати деякому вектору в\(\mathbb{R}^2\). Поясніть, чому буде більше однієї такої матриці\(A\), яка буде доставляти зворотний ізоморфізм\(T^{−1}\)\(im(T)\).

Вправа\(\PageIndex{59}\)

Тепер давайте\(V\) рівнятися\(span\left\{\left[\begin{array}{c}1\\0\\1\end{array}\right],\:\left[\begin{array}{c}0\\1\\1\end{array}\right]\right\}\) і нехай\(T\):\(V\to W\) бути лінійним перетворенням, де\[W=span\left\{\left[\begin{array}{c}1\\0\\1\\0\end{array}\right],\:\left[\begin{array}{c}0\\1\\1\\1\end{array}\right]\right\}\nonumber\] і\[T\left[\begin{array}{c}1\\0\\1\end{array}\right]=\left[\begin{array}{c}1\\0\\1\\0\end{array}\right],\:T\left[\begin{array}{c}0\\1\\1\end{array}\right]=\left[\begin{array}{c}0\\1\\1\\1\end{array}\right]\nonumber\] Поясніть, чому\(T\) це ізоморфізм. Визначте матрицю,\(A\) яка при множенні на ліворуч дає той самий результат,\(T\) що\(V\) і матрицю\(B\), яка подає\(T^{−1}\) далі\(W\). Підказка: Ви повинні мати\[A\left[\begin{array}{cc}1&0\\0&1\\1&1\end{array}\right]=\left[\begin{array}{cc}1&0\\0&1\\1&1\\0&1\end{array}\right]\nonumber\] Тепер збільшити\(\left[\begin{array}{c}1\\0\\1\end{array}\right],\:\left[\begin{array}{c}0\\1\\1\end{array}\right]\), щоб отримати основу для\(\mathbb{R}^3\). Ви можете додати,\(\left[\begin{array}{c}0\\0\\1\end{array}\right]\) наприклад, а потім вибрати інший вектор в\(\mathbb{R}^4\) і нехай\(A\left[\begin{array}{c}0\\0\\1\end{array}\right]\) дорівнює цьому іншому вектору. Тоді ви б\[A\left[\begin{array}{ccc}1&0&0\\0&1&0\\1&1&1\end{array}\right]=\left[\begin{array}{ccc}1&0&0\\0&1&0\\1&1&0\\0&1&1\end{array}\right]\nonumber\] це передбачало б вибір для нового вектора в\(\mathbb{R}^4\) векторі\(\left[\begin{array}{cccc}0&0&0&1\end{array}\right]^T\). Тоді ви могли б знайти\(A\). Ви можете зробити щось подібне, щоб знайти матрицю для\(T^{−1}\) позначеного як\(B\).

Вправа\(\PageIndex{60}\)

Нехай\(V=\mathbb{R}^3\) і нехай\[W=span(S),\text{ where }S=\left\{\left[\begin{array}{r}1\\-1\\1\end{array}\right],\:\left[\begin{array}{r}-2\\2\\-2\end{array}\right],\:\left[\begin{array}{r}-1\\1\\1\end{array}\right],\:\left[\begin{array}{r}1\\-1\\3\end{array}\right]\right\}\nonumber\] Знайти основу\(W\) складається з векторів в\(S\).

Відповідь

У цьому випадку\(\text{dim}(W) = 1\) і основу для складання\(W\) векторів в\(S\) можна отримати, взявши будь-який (ненульовий) вектор з\(S\).

Вправа\(\PageIndex{61}\)

\(T\)Дозволяти лінійне перетворення, задане\[T\left[\begin{array}{c}x\\y\end{array}\right]=\left[\begin{array}{cc}1&1\\1&1\end{array}\right]\left[\begin{array}{c}x\\y\end{array}\right]\nonumber\] Знайти основу для\(\text{ker}(T)\) і\(im(T)\).

Відповідь

Основа для\(\text{ker}(T)\) є\(\left\{\left[\begin{array}{r}1\\-1\end{array}\right]\right\}\) і основа для\(im(T)\) є\(\left\{\left[\begin{array}{c}1\\1\end{array}\right]\right\}\). Є багато інших можливостей для конкретних баз, але в даному випадку\(\text{dim}(\text{ker}(T))=1\) і\(\text{dim}(im(T))=1\).

Вправа\(\PageIndex{62}\)

\(T\)Дозволяти лінійне перетворення, задане\[T\left[\begin{array}{c}x\\y\end{array}\right]=\left[\begin{array}{cc}1&0\\1&1\end{array}\right]\left[\begin{array}{c}x\\y\end{array}\right]\nonumber\] Знайти основу для\(\text{ker}(T)\) і\(im(T)\).

Відповідь

У цьому випадку\(\text{ker}(T)=\{0\}\) і\(im(T)=\mathbb{R}^2\) (підібрати будь-яку основу\(\mathbb{R}^2\)).

Вправа\(\PageIndex{63}\)

Нехай\(V=\mathbb{R}^3\) і нехай\[W=span\left\{\left[\begin{array}{c}1\\1\\1\end{array}\right],\:\left[\begin{array}{r}-1\\2\\-1\end{array}\right]\right\}\nonumber\] Розширити цю основу\(W\) до основи\(V\).

Відповідь

Існує багато можливих таких розширень, одне є (звідки ми знаємо?) :\[\left\{\left[\begin{array}{c}1\\1\\1\end{array}\right],\:\left[\begin{array}{r}-1\\2\\-1\end{array}\right],\:\left[\begin{array}{c}0\\0\\1\end{array}\right]\right\}\nonumber\]

Вправа\(\PageIndex{64}\)

\(T\)Дозволяти лінійне перетворення, задане\[T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{ccc}1&1&1\\1&1&1\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]\nonumber\] What is\(\text{dim}(\text{ker}(T))\)?

Відповідь

Ми можемо легко це побачити, і\(\text{dim}(im(T))=1\), таким чином\(\text{dim}(\text{ker}(T))=3-\text{dim}(im(T))=3-1=2\).

Вправа\(\PageIndex{65}\)

\(B=\left\{\left[\begin{array}{r}2\\-1\end{array}\right],\:\left[\begin{array}{r}3\\2\end{array}\right]\right\}\)Дозволяти бути основою\(\mathbb{R}^2\) і нехай\(\vec{x}=\left[\begin{array}{r}5\\-7\end{array}\right]\) бути вектор в\(\mathbb{R}^2\). Знайти\(C_B(\vec{x})\).

Вправа\(\PageIndex{66}\)

\(B=\left\{\left[\begin{array}{r}1\\-1\\2\end{array}\right],\:\left[\begin{array}{r}2\\1\\2\end{array}\right],\:\left[\begin{array}{r}-1\\0\\2\end{array}\right]\right\}\)Дозволяти бути основою\(\mathbb{R}^3\) і нехай\(\vec{x}=\left[\begin{array}{r}5\\-1\\4\end{array}\right]\) бути вектор в\(\mathbb{R}^2\). Знайти\(C_B(\vec{x})\).

Відповідь

\(C_B(\vec{x})=\left[\begin{array}{r}2\\1\\-1\end{array}\right]\)

Вправа\(\PageIndex{67}\)

\(\mathbb{R}^2→\mathbb{R}^2\)Дозволяти\(T\): бути лінійним перетворенням, визначеним\(T\left(\left[\begin{array}{c}a\\b\end{array}\right)\right]=\left[\begin{array}{c}a+b\\a-b\end{array}\right]\).

Розглянемо дві основи\[B_1=\{\vec{v}_1,\vec{v}_2\}=\left\{\left[\begin{array}{c}1\\0\end{array}\right],\:\left[\begin{array}{r}-1\\1\end{array}\right]\right\}\nonumber\] і\[B_2=\left\{\left[\begin{array}{c}1\\1\end{array}\right],\:\left[\begin{array}{r}1\\-1\end{array}\right]\right\}\nonumber\]

Знайти матрицю\(M_{B_2,B_1}\) по\(T\) відношенню до основ\(B_1\) і\(B_2\).

Відповідь

\(M_{B_2B_1}=\left[\begin{array}{rr}1&0\\-1&1\end{array}\right]\)

Вправа \(\PageIndex{68}\)

Запишіть множину розв'язків наступної системи у вигляді лінійної комбінації векторів\[\left[\begin{array}{rrr}1&-1&2\\1&-2&1\\3&-4&5\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}0\\0\\0\end{array}\right]\nonumber\]

Відповідь

Рішення таке:\(\left[\begin{array}{r}-3\hat{t} \\ -\hat{t} \\ \hat{t}\end{array}\right],\:\hat{t}_3\in\mathbb{R}\). Основою для рішення простору є\(\left[\begin{array}{r}-3\\-1\\1\end{array}\right]\nonumber\)

Вправа\(\PageIndex{69}\)

За допомогою вправи\(\PageIndex{68}\) знайдіть загальне рішення наступної лінійної системи. \[\left[\begin{array}{rrr}1&-1&2\\1&-2&1\\3&-4&5\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}1\\2\\4\end{array}\right]\nonumber\]

Відповідь

Зверніть увагу, що це має ту ж матрицю, що і вищевказана проблема. Рішення полягає в:\(\left[\begin{array}{r}-3\hat{t}_3 \\ -\hat{t}_3 \\ \hat{t}_3\end{array}\right]+\left[\begin{array}{r}0\\-1\\0\end{array}\right],\:\hat{t}_3\in\mathbb{R}\)

Вправа \(\PageIndex{70}\)

Запишіть множину розв'язків наступної системи у вигляді лінійної комбінації векторів\[\left[\begin{array}{rrr}0&-1&2\\1&-2&1\\1&-4&5\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}0\\0\\0\end{array}\right]\nonumber\]

Відповідь

Рішення таке:\(\left[\begin{array}{c}3\hat{t} \\ 2\hat{t} \\ \hat{t}\end{array}\right]\), Основою є\(\left[\begin{array}{c}3\\2\\1\end{array}\right]\)

Вправа\(\PageIndex{71}\)

За допомогою вправи\(\PageIndex{70}\) знайдіть загальне рішення наступної лінійної системи. \[\left[\begin{array}{rrr}0&-1&2\\1&-2&1\\1&-4&5\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}1\\-1\\1\end{array}\right]\nonumber\]

Відповідь

Рішення полягає в:\(\left[\begin{array}{c}3\hat{t} \\ 2\hat{t} \\ \hat{t}\end{array}\right] +\left[\begin{array}{c}-3\\-1\\0\end{array}\right],\:\hat{t}\in\mathbb{R}\)

Вправа \(\PageIndex{72}\)

Запишіть набір розв'язків наступної системи у вигляді лінійної комбінації векторів. \[\left[\begin{array}{ccc}1&-1&2\\1&-2&0\\3&-4&4\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}0\\0\\0\end{array}\right]\nonumber\]

Відповідь

Рішення таке:\(\left[\begin{array}{r}-4\hat{t} \\ -2\hat{t} \\ \hat{t}\end{array}\right]\). Основою є\(\left[\begin{array}{r}-4\\-2\\1\end{array}\right]\)

Вправа\(\PageIndex{73}\)

За допомогою вправи\(\PageIndex{72}\) знайдіть загальне рішення наступної лінійної системи. \[\left[\begin{array}{ccc}1&-1&2\\1&-2&0\\3&-4&4\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}1\\2\\4\end{array}\right]\nonumber\]

Відповідь

Рішення полягає в:\(\left[\begin{array}{r}-4\hat{t} \\ -2\hat{t} \\ \hat{t}\end{array}\right]+\left[\begin{array}{r}0\\-1\\0\end{array}\right],\:\hat{t}\in\mathbb{R}\)

Вправа \(\PageIndex{74}\)

Запишіть множину розв'язків наступної системи у вигляді лінійної комбінації векторів\[\left[\begin{array}{ccc}0&-1&2\\1&0&1\\1&-2&5\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}0\\0\\0\end{array}\right]\nonumber\]

Відповідь

Рішення полягає в:\(\left[\begin{array}{r}-\hat{t} \\ 2\hat{t} \\ \hat{t}\end{array}\right],\:\hat{t}\in\mathbb{R}\)

Вправа\(\PageIndex{75}\)

За допомогою вправи\(\PageIndex{74}\) знайдіть загальне рішення наступної лінійної системи. \[\left[\begin{array}{ccc}0&-1&2\\1&0&1\\1&-2&5\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}1\\-1\\1\end{array}\right]\nonumber\]

Відповідь

Рішення полягає в:\(\left[\begin{array}{r}-\hat{t} \\ 2\hat{t} \\ \hat{t}\end{array}\right]+\left[\begin{array}{r}-1\\-1\\0\end{array}\right]\)

Вправа \(\PageIndex{76}\)

Запишіть множину розв'язків наступної системи у вигляді лінійної комбінації векторів\[\left[\begin{array}{cccc}1&0&1&1\\1&-1&1&0\\3&-1&3&2\\3&3&0&3\end{array}\right]\left[\begin{array}{c}x\\y\\z\\w\end{array}\right]=\left[\begin{array}{c}0\\0\\0\\0\end{array}\right]\nonumber\]

Відповідь

Рішення полягає в:\(\left[\begin{array}{r}0\\ -\hat{t} \\ -\hat{t} \\ \hat{t}\end{array}\right],\:\hat{t}\in\mathbb{R}\)

Вправа\(\PageIndex{77}\)

За допомогою вправи\(\PageIndex{76}\) знайдіть загальне рішення наступної лінійної системи. \[\left[\begin{array}{cccc}1&0&1&1\\1&-1&1&0\\3&-1&3&2\\3&3&0&3\end{array}\right]\left[\begin{array}{c}x\\y\\z\\w\end{array}\right]=\left[\begin{array}{c}1\\2\\4\\3\end{array}\right]\nonumber\]

Відповідь

Рішення полягає в:\(\left[\begin{array}{r}0\\ -\hat{t} \\ -\hat{t} \\ \hat{t}\end{array}\right]+\left[\begin{array}{r}2\\-1\\-1\\0\end{array}\right]\)

Вправа \(\PageIndex{78}\)

Запишіть множину розв'язків наступної системи у вигляді лінійної комбінації векторів\[\left[\begin{array}{cccc}1&1&0&1\\2&1&1&2\\1&0&1&1\\0&0&0&0\end{array}\right]\left[\begin{array}{c}x\\y\\z\\w\end{array}\right]=\left[\begin{array}{c}0\\0\\0\\0\end{array}\right]\nonumber\]

Відповідь

Рішення таке:\(\left[\begin{array}{c}-s-t \\ s\\s\\t\end{array}\right],\:s,t\in\mathbb{R}\). Основою є\[\left\{\left[\begin{array}{r}-1\\1\\1\\0\end{array}\right],\:\left[\begin{array}{r}-1\\0\\0\\1\end{array}\right]\right\}\nonumber\]

Вправа\(\PageIndex{79}\)

За допомогою вправи\(\PageIndex{78}\) знайдіть загальне рішення наступної лінійної системи. \[\left[\begin{array}{rrrr}1&1&0&1\\2&1&1&2\\1&0&1&1\\0&-1&1&1\end{array}\right]\left[\begin{array}{c}x\\y\\z\\w\end{array}\right]=\left[\begin{array}{r}2\\-1\\-3\\0\end{array}\right]\nonumber\]

Відповідь

Рішення полягає в:\[\left[\begin{array}{r}-\hat{t}\\ \hat{t} \\ \hat{t}\\0\end{array}\right]+\left[\begin{array}{c}-8\\5\\0\\5\end{array}\right]\nonumber\]

Вправа \(\PageIndex{80}\)

Запишіть множину розв'язків наступної системи у вигляді лінійної комбінації векторів\[\left[\begin{array}{rrrr}1&1&0&1\\1&-1&1&0\\3&1&1&2\\3&3&0&3\end{array}\right]\left[\begin{array}{c}x\\y\\z\\w\end{array}\right]=\left[\begin{array}{c}0\\0\\0\\0\end{array}\right]\nonumber\]

Відповідь

Рішення таке:\[\left[\begin{array}{c}-\frac{1}{2}s-\frac{1}{2}t \\ \frac{1}{2}s-\frac{1}{2}t \\ s\\t\end{array}\right]\nonumber\] для\(s,t\in\mathbb{R}\). Основою є\[\left\{\left[\begin{array}{r}-1\\1\\2\\0\end{array}\right],\:\left[\begin{array}{r}-1\\1\\0\\1\end{array}\right]\right\}\nonumber\]

Вправа\(\PageIndex{81}\)

За допомогою вправи\(\PageIndex{80}\) знайдіть загальне рішення наступної лінійної системи. \[\left[\begin{array}{rrrr}1&1&0&1\\1&-1&1&0\\3&1&1&2\\3&3&0&3\end{array}\right]\left[\begin{array}{c}x\\y\\z\\w\end{array}\right]=\left[\begin{array}{c}1\\2\\4\\3\end{array}\right]\nonumber\]

Відповідь

Рішення полягає в:\[\left[\begin{array}{r}\frac{3}{2} \\ -\frac{1}{2}\\0\\0\end{array}\right]+\left[\begin{array}{c}-\frac{1}{2}s-\frac{1}{2}t \\ \frac{1}{2}s-\frac{1}{2}t \\ s\\t\end{array}\right]\nonumber\]

Вправа \(\PageIndex{82}\)

Запишіть множину розв'язків наступної системи у вигляді лінійної комбінації векторів\[\left[\begin{array}{rrrr}1&1&0&1\\2&1&1&2\\1&0&1&1\\0&-1&1&1\end{array}\right]\left[\begin{array}{c}x\\y\\z\\w\end{array}\right]=\left[\begin{array}{c}0\\0\\0\\0\end{array}\right]\nonumber\]

Відповідь

Рішення таке:\(\left[\begin{array}{r}-\hat{t} \\ \hat{t} \\ \hat{t}\\0\end{array}\right]\), основа є\(\left[\begin{array}{c}1\\1\\1\\0\end{array}\right]\).

Вправа\(\PageIndex{83}\)

За допомогою вправи\(\PageIndex{82}\) знайдіть загальне рішення наступної лінійної системи. \[\left[\begin{array}{rrrr}1&1&0&1\\2&1&1&2\\1&0&1&1\\0&-1&1&1\end{array}\right]\left[\begin{array}{c}x\\y\\z\\w\end{array}\right]=\left[\begin{array}{r}2\\-1\\-3\\1\end{array}\right]\nonumber\]

Відповідь

Рішення таке:\(\left[\begin{array}{r}-\hat{t} \\ \hat{t} \\ \hat{t}\\0\end{array}\right]+\left[\begin{array}{r}-9\\5\\0\\6\end{array}\right],t\in\mathbb{R}\).

Вправа\(\PageIndex{84}\)

\(A\vec{x}=\vec{b}\)Припустимо, є рішення. Поясніть, чому рішення унікальне саме тоді, коли\(A\vec{x}=\vec{0}\) має лише тривіальне рішення.

Відповідь

Якщо ні, то було б нескінченно багато рішень,\(A\vec{x}=\vec{0}\) і кожне з них додано до рішення, яке\(A\vec{x}=\vec{b}\) буде рішенням\(A\vec{x}=\vec{b}\).