1.3: Хрестовий продукт

Last updated
Save as PDF

Page ID: 60562

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Як ми зазначали в Розділі 1.1, немає загального способу визначення множення для векторів в\(\mathbb{R}^{n}\), при цьому добуток також є вектором тієї ж розмірності, що корисно для наших цілей у цій книзі. Однак в особливому випадку\(\mathbb{R}^{3}\) є продукт, який ми знайдемо корисним. Однією з мотивацій для цього продукту є розгляд наступної проблеми: з урахуванням двох векторів\(\mathbf{x}=\left(x_{1}, x_{2}, x_{3}\right)\) і\(\mathbf{y}=\left(y_{1}, y_{2}, y_{3}\right)\) в\(\mathbb{R}^{3}\), не паралельно один одному, знайти третій вектор\(\mathbf{w}=\left(w_{1}, w_{2}, w_{3}\right)\), ортогональний обох\(\mathbf{x}\) і\(\mathbf{y}\). Таким чином ми хочемо\(\mathbf{w} \cdot \mathbf{x}=0\) і\(\mathbf{w} \cdot \mathbf{y}=0\), а значить, нам потрібно вирішити рівняння

\[x_1w_1 + x_2w_2+x_3w_3=0 \\ y_1w_1 + y_2w_2+y_3w_3=0 \label{1.3.1}\]

для\(w_1\),\(w_2\), і\(w_3\). Множення першого рівняння на,\(y_3\) а друге на\(x_3\) дає нам

\[x_1y_3w_1 + x_2y_3w_2 + x_3y_3w_3 = 0 \\ x_3y_1w_1 + x_3y_2w_2 + x_3y_3w_3 = 0 . \label{1.3.2} \]

Віднімаючи друге рівняння з першого, ми маємо

\[ (x_1y_3-x_3y_1)w_1 + (x_2y_3-x_3y_2)w_2=0 . \label{1.3.3}\]

Один розв'язок рівняння\ ref {1.3.3} задається установкою

\[w_1=x_2y_3-x_3y_2 \\ w_2=-(x_1y_3-x_3y_1) = x_3y_1-x_1y_3 . \label{1.3.4}\]

Нарешті, з першого рівняння в Equation\ ref {1.3.1}, ми тепер маємо

\[x_3w_3=-x_1(x_2y_3-x_3y_2)-x_2(x_3y_1-x_1y_3)=x_1x_3y_2-x_2x_3y_1 , \label{1.3.5}\]

з якого отримуємо розчин

\[w_3=x_1y_2-x_2y_1 . \label{1.3.6}\]

Вибір, зроблений при отриманні Equation\ ref {1.3.4} і\ ref {1.3.6}, не є унікальним, але вони є стандартними варіантами, які визначають\(\mathbf{w}\) як перехресний або векторний добуток\(\mathbf{x}\) і\(\mathbf{y}\).

Визначення\(\PageIndex{1}\)

Задані вектори\(\mathbf{x}=\left(x_{1}, x_{2}, x_{3}\right)\) і\(\mathbf{y}=\left(y_{1}, y_{2}, y_{3}\right)\) in\(\mathbb{R}^{3}\), вектор

\[ \mathbf{x}\times \mathbf{y}=(x_2y_3-x_3y_2,x_3y_1-x_1y_3,x_1y_2-x_2y_1)\]

називається перехресним добутком, або векторним добутком,\(\mathbf{x}\) і\(\mathbf{y}\).

Приклад\(\PageIndex{1}\)

Якщо\(\mathbf{x}=(1,2,3)\) і\(\mathbf{y}=(1,-1,1)\), то

\[\mathbf{x} \times \mathbf{y} = (2 + 3,3 − 1,−1 − 2) = (5,2,−3) . \nonumber \]

Зауважте, що

\[\mathbf{x} \cdot (\mathbf{x} \times \mathbf{y}) = 5+4-9=0 \nonumber\]

\[\mathbf{y} \cdot (\mathbf{x} \times \mathbf{y})=5-2-3=0 , \nonumber \]

показуючи, що\(\mathbf{x} \perp (\mathbf{x} \times \mathbf{y})\) і\( \mathbf{y} \perp (\mathbf{x} \times \mathbf{y}) \) як стверджувалося. Також цікаво відзначити, що

\[\mathbf{y}\times \mathbf{x}=(-3-2,1-3,2+1)=(-5,-2,3)=-(\mathbf{x}\times \mathbf{y}) . \nonumber\]

Це останнє обчислення проводиться в цілому для всіх векторів\(\mathbf{x}\) і\(\mathbf{y}\) в\(\mathbb{R}^{3}\).

Пропозиція\(\PageIndex{1}\)

Припустимо\(\mathbf{x}\)\(\mathbf{y}\), і\(\mathbf{z}\) є векторами в\(\mathbb{R}^3\) і\(\alpha\) є будь-яким дійсним числом. Тоді

\[\mathbf{x}\times \mathbf{y} = -(\mathbf{y} \times \mathbf{x}) , \]

\[\mathbf{x} \times (\mathbf{y}+\mathbf{z}) = (\mathbf{x} \times \mathbf{y}) + (\mathbf{x} \times \mathbf{z}) , \]

\[(\mathbf{x}+\mathbf{y}) \times \mathbf{z} = (\mathbf{x} \times \mathbf{z}) + (\mathbf{y} \times \mathbf{z}) , \]

\[ \alpha (\mathbf{x} \times \mathbf{y}) = (\alpha \mathbf{x}) \times \mathbf{y} = \mathbf{x} \times (\alpha \mathbf{y}) , \]

\[\mathbf{x} \times \mathbf{0} = \mathbf{0} . \]

Перевірка цих властивостей проста і буде залишена до вправи 10. Крім того, зверніть увагу, що

\[\mathbf{e}_1 \times \mathbf{e}_2 = \mathbf{e}_3 , \]

\[\mathbf{e}_2 \times \mathbf{e}_3 = \mathbf{e}_1 , \]

\[\mathbf{e}_3 \times \mathbf{e}_1 = \mathbf{e}_2 ; \]

тобто перехресний добуток двох стандартних базисних векторів є або іншим стандартним базисним вектором, або його негативним. Крім того, зверніть увагу, що в цих випадках перехресний продукт вказує в напрямку, який буде вказувати великий палець, якби ви обернули пальці правої руки від першого вектора до другого. Це насправді завжди вірно і призводить до того, що відоме як правило правої руки для орієнтації поперечного виробу, як показано на малюнку 1.3.1. Звідси дано два вектори\(\mathbf{x}\) і\(\mathbf{y}\), ми завжди можемо визначити напрямок\(\mathbf{x} \times \mathbf{y}\); до

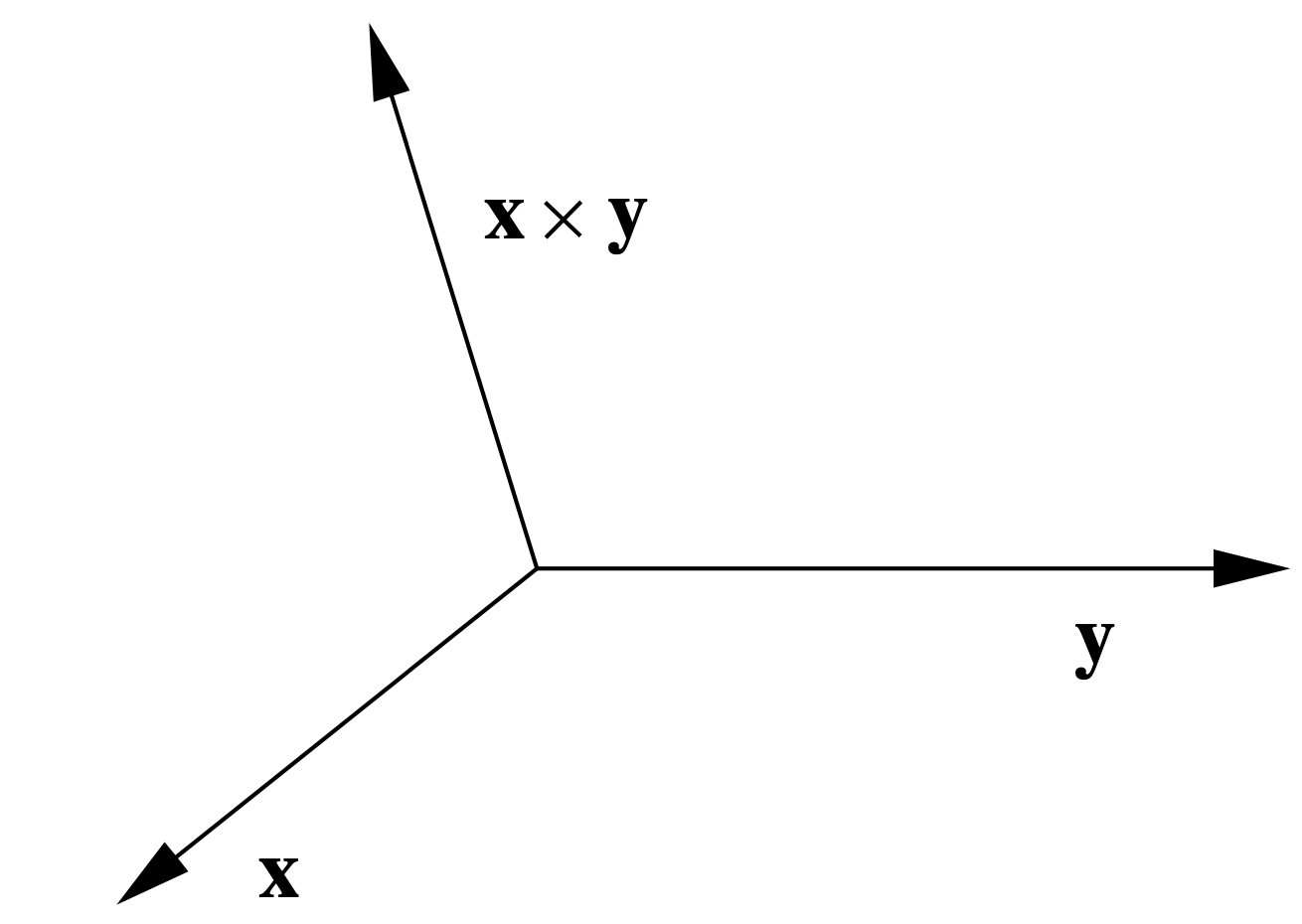
Знімок екрана 2021-07-17 о 17.49.51.png — Малюнок\(\PageIndex{1}\): Правило правої руки

повністю ідентифікувати\(\mathbf{x} \times \mathbf{y}\) геометрично, потрібно лише знати її довжину. Тепер, якщо θ - кут між\(\mathbf{x}\) і\(\mathbf{y}\), то

\ почати {вирівняти}
\ |\ mathbf {x}\ раз\ mathbf {y}\ |^ {2} =&\ ліворуч (x_ {2} y_ {3} -x_ {3} y_ {2}\ праворуч) ^ {2} +\ ліворуч (x_ {3} y_ {1} -x_ {1} y_ {3} y_ {3} y_ {3} y_ {3} y_ {3} y_ {3} 2} +\ лівий (x_ {1} y_ {2} -x_ {2} y_ {1}\ праворуч) ^ {2}\ номер\
=& x_ {2} ^ {2} y_ {3} ^ {2} -2 x_ {2} x_ {3} y_ {2} y_ {2} y_ {3} +x_ {3} ^ {2} y_ 2} ^ {2} +x_ {3} ^ {2} y_ {1} ^ {2} -2 x_ {1} x_ {3} y_ {1} y_ {3} +x_ {1} ^ {2} y_ {3} ^ {2} +x_ {1} ^ {2} y_ {2} ^ {2}\ номер\\
&\ квадра-2 x_ {1} x_ {2} x_ {2} y_ {1} y_ {1} y_ {2} y_ {2}} ^ {2} y_ {1} ^ {2}\ номер\
= &\ ліворуч (x_ {1} ^ {2} +x_ {2} ^ {2} +x_ {3} ^ {2}\ праворуч)\ лівий (y_ {1} ^ {2} +y_ {2} ^ {2} +y_ {3} ^ {2} ^ {3} ^ {2} ^ {2} ^ {2} +y_ {3} ^ {2} ^ {2} ліворуч (x_ {1} ^ {2} y_ {1} ^ {2} +x_ {2} ^ {2} y_ {2} ^ {2} +x_ {3} ^ {2} y_ {3} ^ {2}\ праворуч)\ номер\\
&\ quad-\ ліворуч (2 x_ {2} x_ {3} y_ {2} y_ {3} +2 x_ {1} x_ {3} y_ {1} y_ {3} +2 x_ {1} x_ {2} 1} y_ {2}\ праворуч)\ номер\
= &\ ліворуч (x_ {1} ^ {2} +x_ {2} ^ {2} +x_ {3} ^ {2} ^ {2} ^ {2} +y_ {2} ^ {2} +y_ {2} +y_ {3} ^ {2} ^ {2} ^ {2} ^ {2} ^ {2} {1} y_ {1} +x_ {2} y_ {2} +x_ { 3} y_ {3}\ праворуч) ^ {2}\ номер\
=&\ |\ mathbf {x}\ |^ {2}\ |\ mathbf {y}\ |^ {2} - (\ mathbf {x}\ cdot\ mathbf {y}) ^ {2}\ nonnumber\
=\\ |\ mathbf f {x}\ |^ {2}\ |\ mathbf {y}\ |^ {2} - (\ |\ mathbf {x}\ |\ mathbf {y}\ |\ cos (\ тета)) ^ {2}\ номер\
=&\ |\ mathbf {x} |^ {2}\\ mathbf {y}\ |^ {2 }\ ліворуч (1-\ cos ^ {2} (\ тета)\ праворуч)\ номер\
= &\\ |\ mathbf {x}\ |^ {2}\ |\ mathbf {y}\ |^ {2}\ sin ^ {2} (\ тета). \ етикетка {}
\ end {вирівнювання}

Беручи квадратні корені, і зауваживши, що\(\sin(\theta) \geq 0 \) оскільки, за визначенням кута між двома векторами\(0 \leq \theta \leq \pi \), ми маємо наступний результат.

Пропозиція\(\PageIndex{2}\)

Якщо θ - кут між двома векторами\(\mathbf{x}\) і\(\mathbf{y}\) in\(\mathbb{R}^{3}\), то

\[ \| \mathbf{x} \times \mathbf{y} \| = \| \mathbf{x} \| \| \mathbf{y} \| \sin (\theta) . \label{1.3.17} \]

Остання теорема має кілька цікавих наслідків. Один з них походить від визнання того, що якщо ми намалюємо паралелограм з\(\mathbf{x}\) і\(\mathbf{y}\) як сусідні сторони, як на малюнку 1.3.2, то висота паралелограма є\(\| \mathbf{y} \| \sin(\theta)\), де θ - кут між\(\mathbf{x}\) і\(\mathbf{y}\). Звідси площа паралелограма дорівнює\(\| \mathbf{x} \| \| \mathbf{y} \| \sin(\theta)\), яка за рівнянням\ ref {1.3.17} є\(\| \mathbf{x} \times \mathbf{y} \|\).

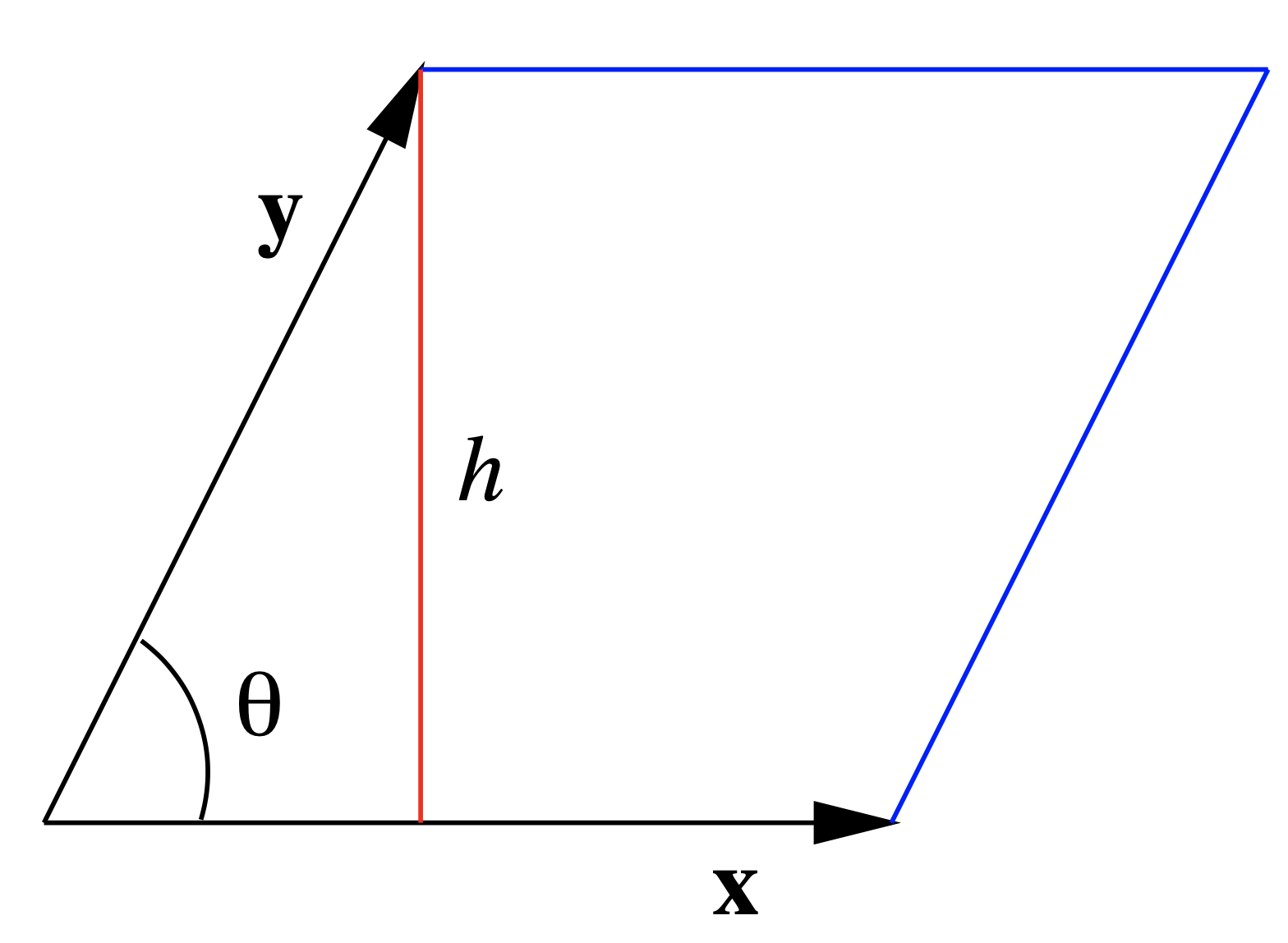
Знімок екрана 2021-07-17 о 18.06.10.png — Малюнок\(\PageIndex{2}\): Висота паралелограма дорівнює\(h=\| \mathbf{y} \| \sin(\theta)\)

Пропозиція\(\PageIndex{3}\)

Припустимо\(\mathbf{y}\),\(\mathbf{x}\) і є двома векторами в\(\mathbb{R}^{3}\). Тоді площа паралелограма, який має\(\mathbf{x}\) і\(\mathbf{y}\) для суміжних сторін, дорівнює\(\| \mathbf{x} \times \mathbf{y} \| \).

Приклад\(\PageIndex{2}\)

Розглянемо паралелограм\(P\) з вершинами в (0, 0, 0), (6, 1, 1), (8, 5, 2), і (2, 4, 1). Дві сусідні сторони задаються векторами\(\mathbf{x}=(6,1,1)\) і\(\mathbf{y}=(2,4,1)\) (див. Рис\(P\).

\[\| \mathbf{x} \times \mathbf{y} \| = \|(1-4,2-6,24-2) \| = \| (-3,-4,22 \| = \sqrt{509} . \nonumber \]

Див. Рисунок 1.3.4, щоб побачити зв'язок між\(\mathbf{x} \times \mathbf{y}\) і\(P\).

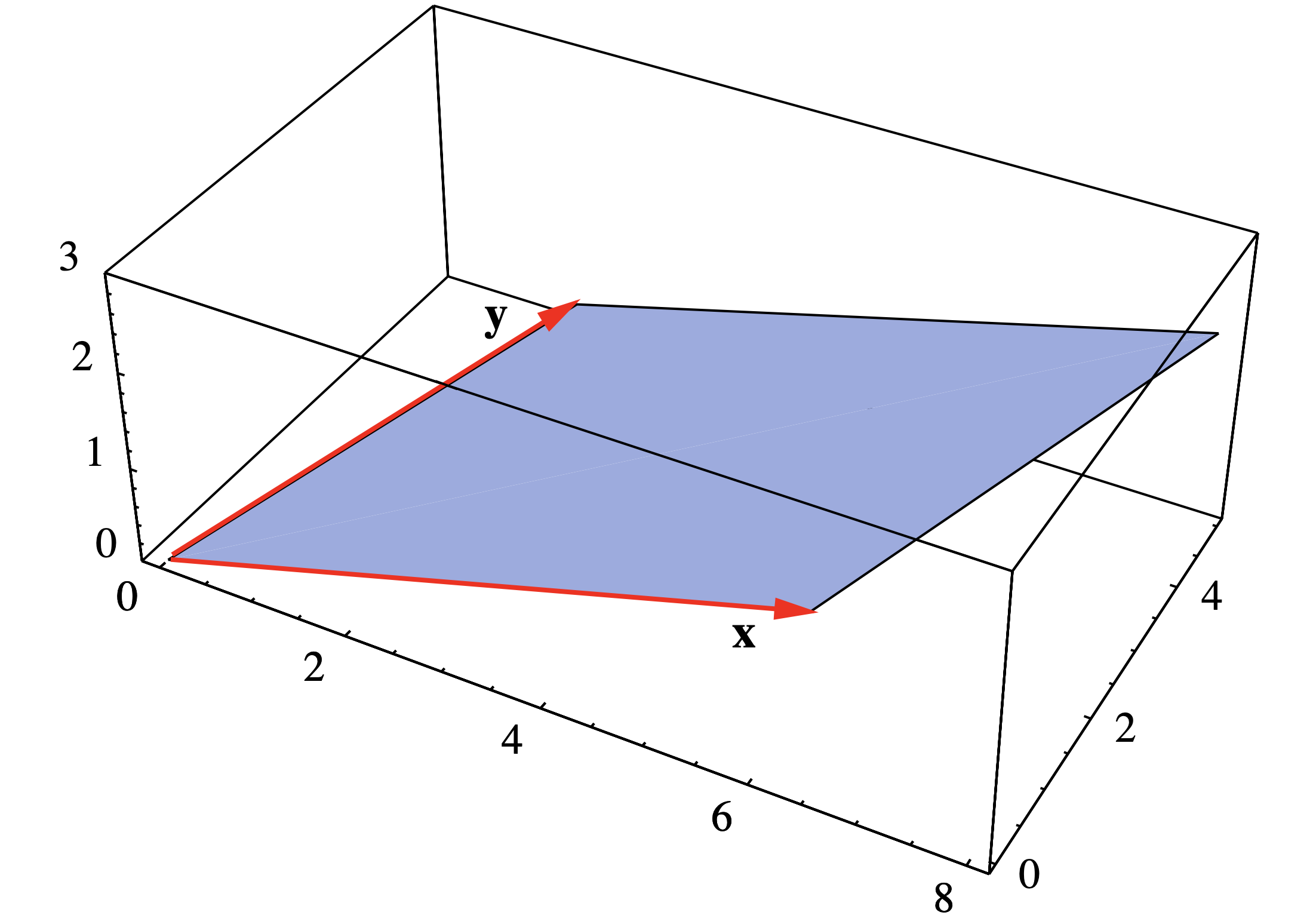
Знімок екрана 2021-07-17 о 18.08.09.png — Малюнок\(\PageIndex{3}\): Паралелограм з вершинами в (0, 0, 0), (6, 1, 1), (8, 5, 2), і (2, 4, 1)

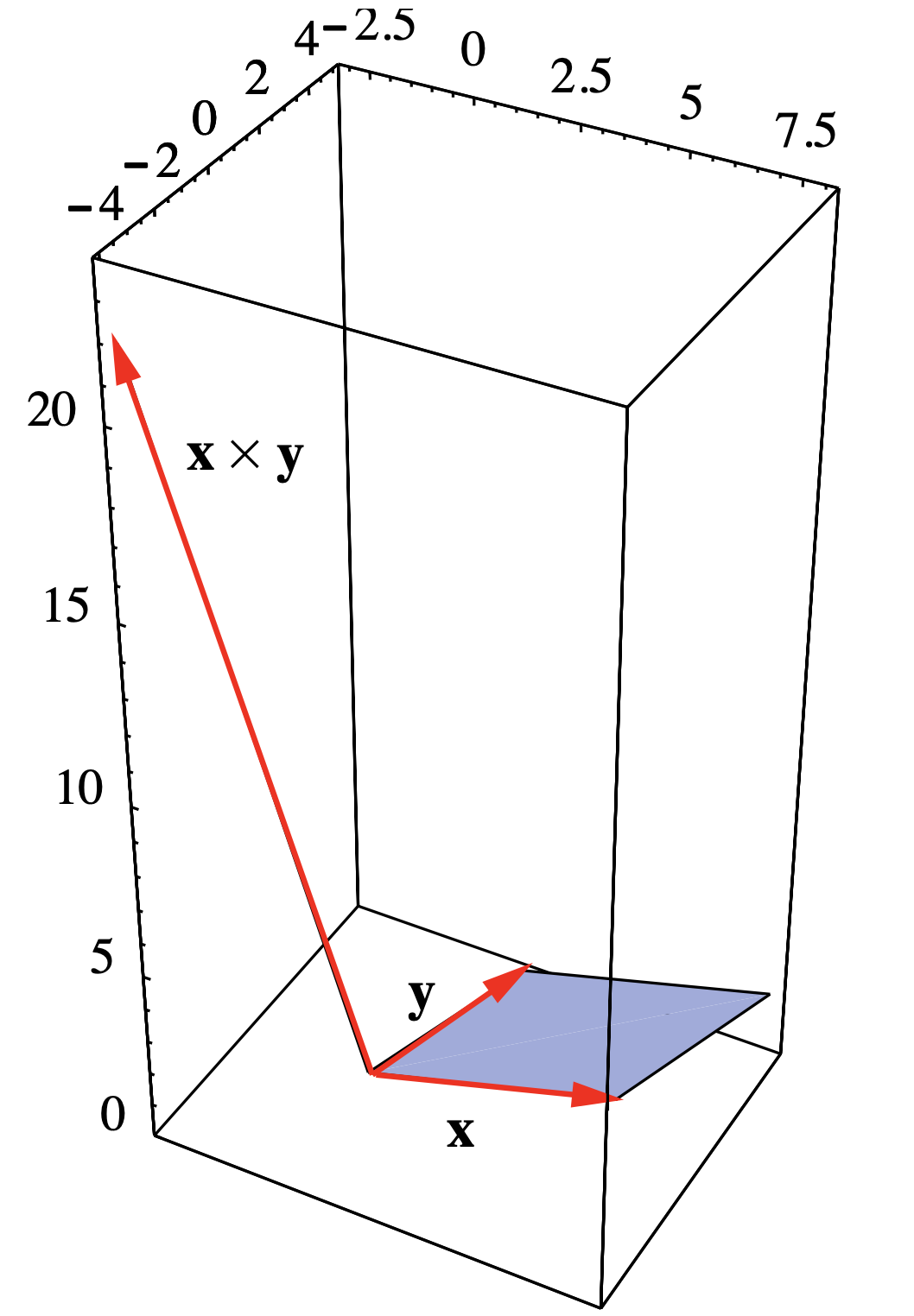
Знімок екрана 2021-07-17 о 18.20.13.png — Малюнок 1.3.4 Паралелограм з суміжними сторонами\(\mathbf{x}=(6,1,1)\) і\(\mathbf{y}=(2,4,1)\)

Приклад\(\PageIndex{3}\)

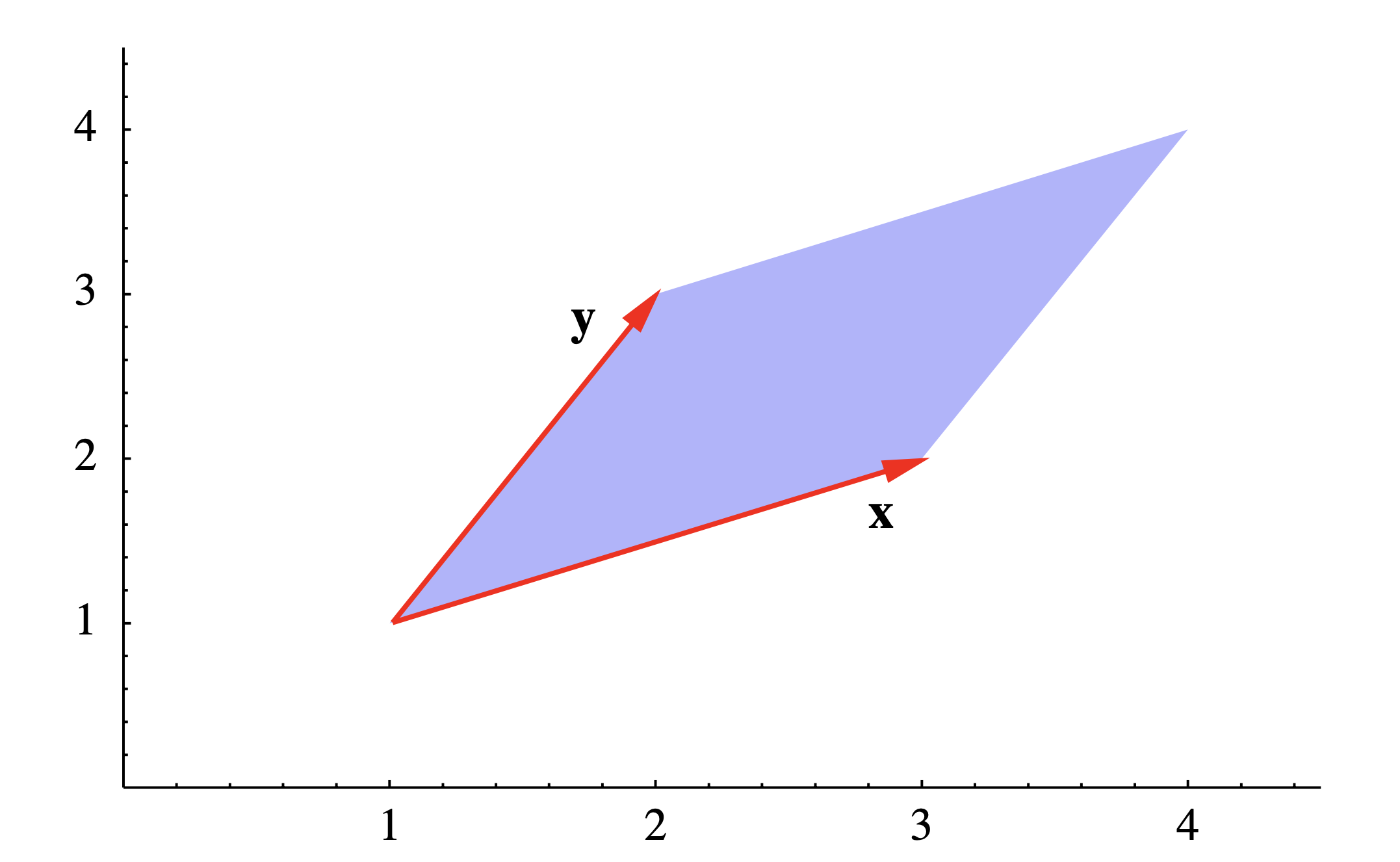
Розглянемо паралелограм\(P\) в площині з вершинами в (1, 1,), (3, 2), (4, 4), і (2, 3). Дві сусідні сторони задаються векторами від (1, 1) до (3, 2), тобто

\[\mathbf{x} = (3,2) - (1,1) = (2,1) , \nonumber \]

і від (1,1) до (2,3), тобто

\[\mathbf{y}=(2,3)-(1,1)=(1,2) . \nonumber\]

Див. Малюнок 1.3.5. Однак, оскільки ці вектори знаходяться в\(\mathbb{R}^2\), а не в\(\mathbb{R}^3\), ми не можемо обчислити їх перехресний добуток. Щоб обійти це, розглянемо вектори\(\mathbf{w}=(2,1,0)\) і\(\mathbf{v}=(1,2,0)\) які є суміжними сторонами того ж паралелограма розглядаються як лежать в\(\mathbb{R}^3\). Тоді площа\(P\) задається\[ \| \mathbf{w} × \mathbf{v} \| = \| (0,0,4 − 1) \| = \| (0,0,3)\| = 3 . \nonumber \]

Знімок екрана 2021-07-17 о 18.20.52.png — Малюнок\(\PageIndex{5}\): Паралелограм з вершинами в (1, 1), (3, 2), (4, 4), і (2, 3)

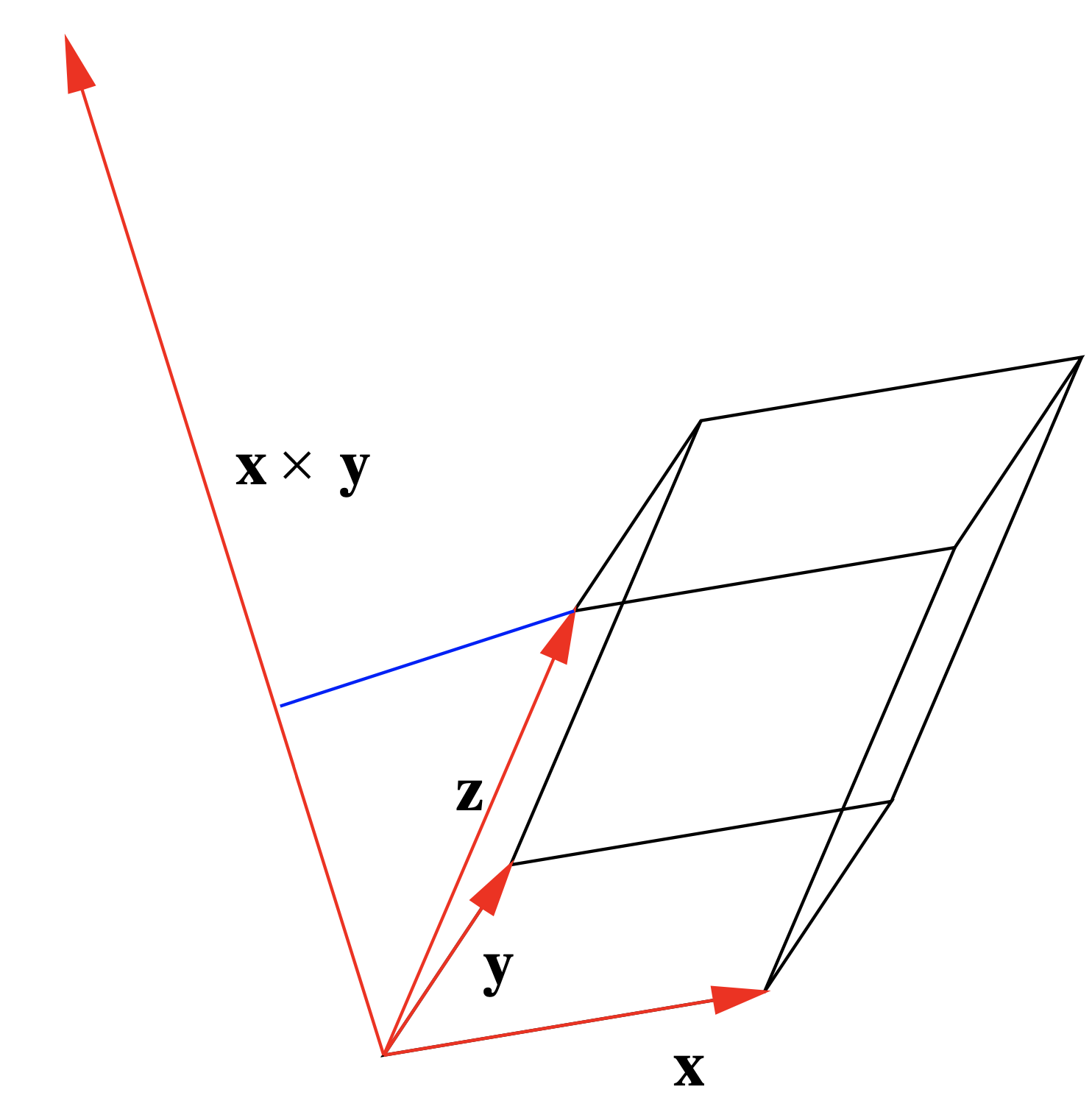
Легко розширити результат попередньої теореми на обчислення обсягу паралелепіпеда в\(\mathbb{R}^3\). Припустимо\(\mathbf{x}\)\(\mathbf{y}\),, і\(\mathbf{z}\) є суміжними краями паралелепіпеда\(P\), як показано на малюнку 1.3.6. Тоді\(V\) обсяг\(P\) є\(\| \mathbf{x} \times \mathbf{y} \| \), який є площею підстави, множиться на висоту\(P\), яка є довжиною проекції\(\mathbf{z}\) на\(\mathbf{x} \times \mathbf{y}\). Так як останній дорівнює

\[ \left| \mathbf{z} \cdot \frac{\mathbf{x} \times \mathbf{y}}{\| \mathbf{x} \times \mathbf{y} \|} \right| , \nonumber \]

Знімок екрана 2021-07-17 о 18.23.33.png — Малюнок\(\PageIndex{6}\): Паралелепіпед з суміжними краями\(\mathbf{x}\)\(\mathbf{y}\), і\(\mathbf{z}\)

у нас є

\[V = \| \mathbf{x} \times \mathbf{y} \| \left| z \cdot \frac{\mathbf{x} \times \mathbf{y}}{\| \mathbf{x} \times \mathbf{y} \|} \right| = \vert \mathbf{z} \cdot (\mathbf{x} \times \mathbf{y}) \vert . \]

Пропозиція\(\PageIndex{4}\)

Обсяг паралелепіпеда з прилеглими краями\(\mathbf{x}\)\(\mathbf{y}\), і\(\mathbf{z}\) є\( \vert \mathbf{z} \cdot (\mathbf{x} \times \mathbf{y}) \vert \).

Визначення\(\PageIndex{2}\)

Дано три вектори\(\mathbf{x}\)\(\mathbf{y}\), і\(\mathbf{z}\) в\(\mathbb{R}^3\), величина\( \mathbf{z} \cdot (\mathbf{x} \times \mathbf{y}) \) називається скалярним потрійним\(\mathbf{x}\) добутком\(\mathbf{y}\), і\(\mathbf{x}\).

Приклад\(\PageIndex{4}\)

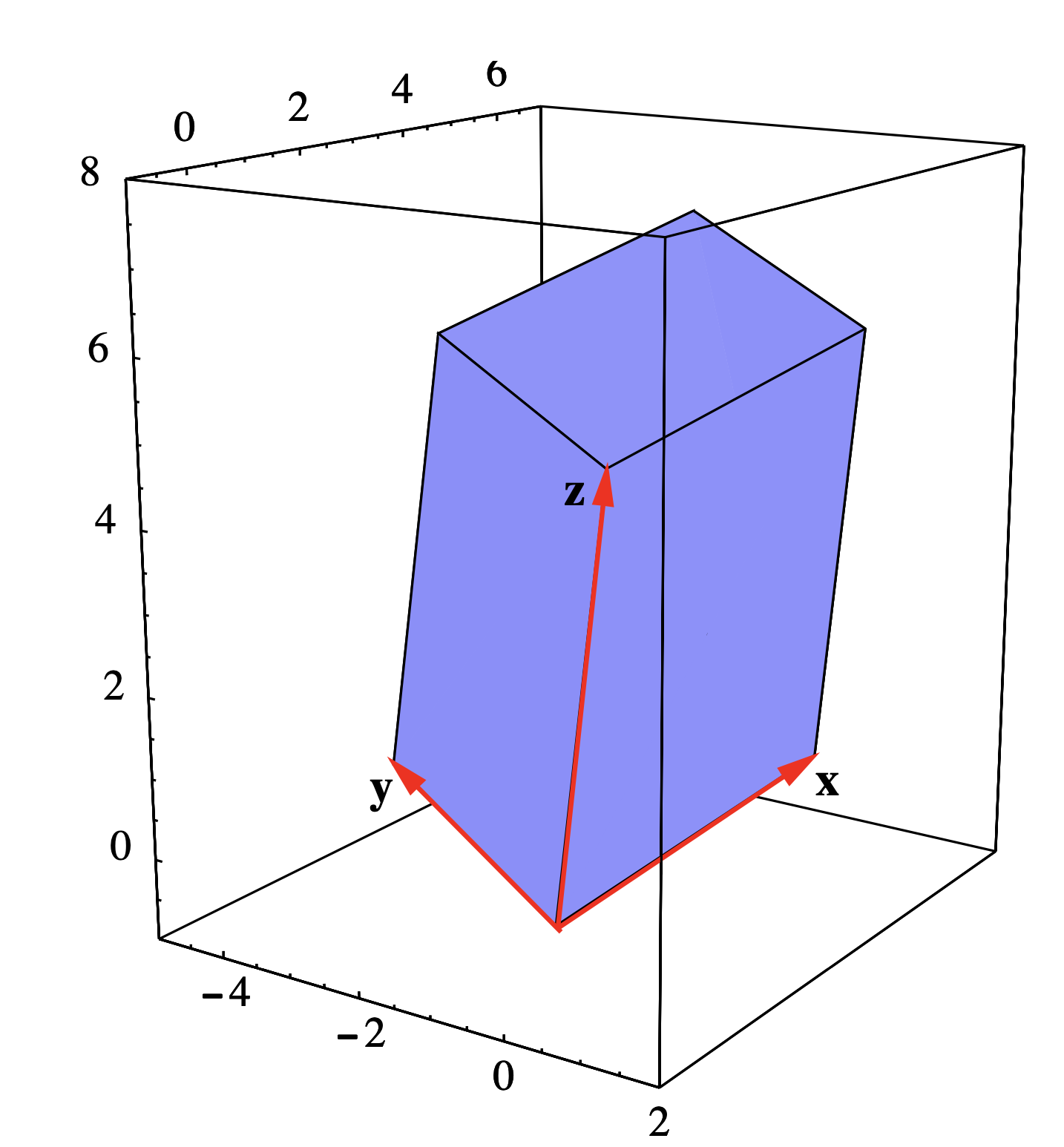
Дозволяти\(\mathbf{x}=(1,4,1)\)\(\mathbf{y}=(-3,1,1)\), і\(\mathbf{z}=(0,1,5)\) бути суміжними краями паралелепіпеда\(P\) (див. Рис. Тоді\[\mathbf{x} \times \mathbf{y} = (4-1,-3-1,1+12) = (3,-4,13) , \nonumber \]

тому

\[\mathbf{z} \cdot (\mathbf{x} \times \mathbf{y}) = 0-4+65 = 61. \nonumber \]

Звідси обсяг\(P\) дорівнює 61.

Знімок екрана 2021-07-17 о 18.45.18.png — Малюнок\(\PageIndex{7}\): Паралелепіпед з сусідніми краями\(\mathbf{x} = (1, 4, 1), \mathbf{y} = (−3, 1, 1), \mathbf{z} = (0, 1, 5)\)

Кінцевий результат цього розділу випливає з Equation\ ref {1.3.17} і той факт, що кут між паралельними векторами дорівнює або 0, або\(\pi\).

Пропозиція\(\PageIndex{5}\)

Вектори\(\mathbf{x}\) і\(\mathbf{y}\) в\(\mathbb{R}^3\) паралельні якщо і тільки якщо\(\mathbf{x} \times \mathbf{y}=\mathbf{0}\).

Відзначимо, що, зокрема, для будь-якого вектора\(\mathbf{x}\) в\(\mathbb{R}^3\),\(\mathbf{x} \times \mathbf{x}=\mathbf{0}\).