Огляд
- Page ID
- 62950
Предмет цього підручника
Перш ніж почати зі змісту тексту, спочатку задаємо основне питання: що таке лінійна алгебра?
- Лінійні: пов'язані з лініями, площинами тощо.
- Алгебра: розв'язування рівнянь за участю невідомих.
Назва підручника виділяє важливу тему: синтез між алгеброю і геометрією. Нам буде дуже важливо розуміти системи лінійних рівнянь як алгебраїчно (написання рівнянь для їх розв'язків), так і геометрично (малювання малюнків і візуалізація).
Термін «алгебра» був придуманий математиком\(9\) го століття Абу Джафар Мухаммад ібн Муса аль-Хорізмі. Воно походить від арабського слова al-jebr, що означає возз'єднання розбитих частин.
На найпростішому рівні вирішити систему лінійних рівнянь не дуже складно. Ви, напевно, дізналися в середній школі, як вирішити таку систему, як
\[\left\{\begin{array}{rrrrrrr}{x}&{+}&{3y}&{-}&{z}&{=}&{4} \\ 2x&-&y&+&3z&=&17 \\ {}&{}&{y}&{-}&{4z}&{=}&{-3.}\end{array}\right. \nonumber\]
Однак у реальному житті зазвичай доводиться бути розумнішими.
- Інженерам потрібно вирішити багато, багато рівнянь у багатьох, багатьох змінних. Ось крихітний приклад:
\[\left\{\begin{array}{rrrrrrrrrrrrr}3x_1 & +&4x_2 &+&10x_3&+&19x_4&-&2x_5&-&3x_6&=&141 \\ 7x_1 &+&2x_2&-&13x_3&-&7x_4&+&21x_5&+&8x_6&=& 2567 \\ -x_1 &+& 9x_2 &+& \frac 32x_3 &+& x_4 &+& 14x_5& + &27x_6 &=& 26 \\ \frac 12x_1 &+& 4x_2 &+& 10x_3 &+& 11x_4 &+& 2x_5 &+& x_6 &=& -15 \end{array}\right. \nonumber\] - Часто досить знати деяку інформацію про сукупність розв'язків, без необхідності вирішувати рівняння в першу чергу. Наприклад, чи існує рішення? Як виглядає набір рішень геометрично? Чи є ще рішення, якщо ми\(26\) змінимо на\(27\text{?}\)
- Іноді коефіцієнти також містять параметри, такі як рівняння власного значення.
\[\left\{\begin{array}{rrrrrrr} (7-\lambda)x &+& y &+& 3z &=& 0 \\ -3x& +& (2-\lambda)y &-& 3z &=& 0 \\ -3x &-& 2y& +& (-1-\lambda)z &=& 0\end{array}\right. \nonumber\] - У моделюванні даних система рівнянь, як правило, фактично не має рішення. У такому випадку, яке найкраще приблизне рішення?
Відповідно, цей текст організований на три основні розділи.
-
Розв'яжіть матричне рівняння\(Ax=b\) (глави 2 — 4).
- Розв'язуйте системи лінійних рівнянь за допомогою матриць, скорочення рядків та обернень.
- Проаналізуйте системи лінійних рівнянь геометрично, використовуючи геометрію множин розв'язків та лінійних перетворень.
-
Розв'яжіть матричне рівняння\(Ax=\lambda x\) (глави 5 — 6).
- Розв'язуйте задачі на власні значення, використовуючи характеристичний многочлен.
- Зрозумійте геометрію матриць за допомогою подібності, власних значень, діагоналізації та комплексних чисел.
-
Приблизно вирішуємо матричне рівняння\(Ax=b\) (глава 7).
- Знайдіть оптимальні рішення для систем лінійних рівнянь, які не мають фактичного розв'язку, використовуючи наближення найменших квадратів.
- Вивчіть геометрію найближчих векторів і ортогональних проекцій.
Цей текст має приблизно наполовину обчислювальний і наполовину концептуальний характер. Основна мета полягає в тому, щоб представити бібліотеку інструментів лінійної алгебри, і, що ще важливіше, навчити концептуальну основу для розуміння того, які інструменти слід застосовувати в даному контексті.
Якщо Matlab може знайти відповідь швидше, ніж ви можете, то ваше питання - це всього лише алгоритм: це не реальне вирішення проблеми.
Тонка частина предмета полягає в розумінні того, які обчислення попросити комп'ютер зробити для вас - набагато менш важливо знати, як виконувати обчислення, які комп'ютер може зробити краще, ніж ви в будь-якому випадку.
Використання лінійної алгебри в техніці
Переважна більшість магістрантів Georgia Tech повинні пройти курс лінійної алгебри. Для цього є причина:
Більшість інженерних завдань, якими б складними не були, можна звести до лінійної алгебри:
\[ Ax=b \quad\text{or}\quad Ax=\lambda x \quad\text{or}\quad Ax\approx b. \nonumber \]
Тут ми наведемо деякі зразки задач в науці та техніці, які потребують лінійної алгебри для розв'язання.
На наступній схемі зображений транспортний потік навколо міської площі. Вулиці всі в одну сторону, а цифри та стрілки вказують на кількість автомобілів на годину, що протікають уздовж кожної вулиці, як вимірюється датчиками під дорогами.
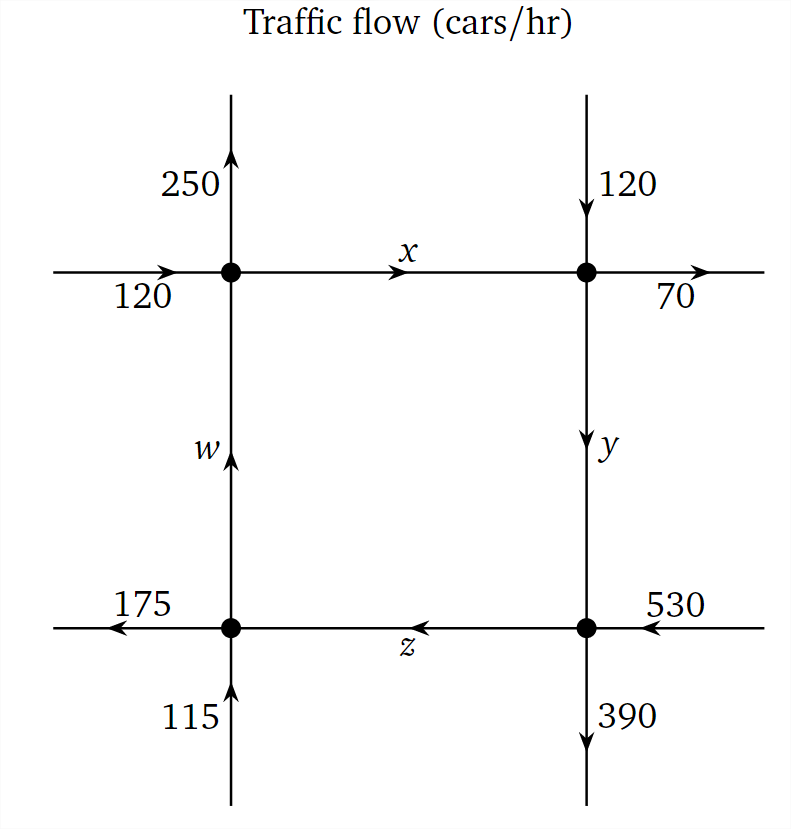
Малюнок\(\PageIndex{1}\)
Під деякими вулицями немає датчиків, тому ми не знаємо, скільки трафіку тече навколо самої площі. Які значення\(x,y,z,w\text{?}\) Оскільки кількість автомобілів, що входять на кожне перехрестя, має дорівнювати кількості автомобілів, що виходять з цього перехрестя, ми отримуємо систему лінійних рівнянь:
\[\left\{\begin{array}{rrrrrrr} w &+& 120 &=& x &+& 250\\ x &+& 120 &=& y &+& 70\\ y &+& 530 &=& z &+& 390\\ z &+& 115 &=& w &+& 175 \end{array}\right.\nonumber\]
Певна хімічна реакція (горіння) приймає етан і кисень, і утворює вуглекислий газ і воду:
\[\underline{x}\:\text{C}_{2}\text{H}_{6}\:+\:\underline{y}\:\text{O}_{2}\:\to\:\underline{z}\:\text{CO}_{2}\:+\:\underline{w}\:\text{H}_{2}\text{O}\nonumber\]
Яке співвідношення молекул необхідно для підтримки реакції? Наступні три рівняння виходять з того, що кількість атомів вуглецю, водню і кисню з лівого боку має дорівнювати числу атомів з правого, відповідно:
\[ \begin{split} 2x \amp= z \\ 6x \amp= 2w \\ 2y \amp= 2z + w\rlap. \end{split} \nonumber \]
У популяції кроликів,
- половина новонароджених кроликів переживає свій перший рік;
- з них половина переживає свій другий рік;
- максимальна тривалість життя - три роки;
- кролики виробляють 0, 6, 8 дитячих кроликів у перший, другий і третій роки відповідно.
Якщо ви знаєте популяцію кроликів в 2016 році (за чисельністю кроликів першого, другого і третього року), то яка популяція в 2017 році? Правила розмноження призводять до наступної системи рівнянь, де\(x,y,z\) представляють чисельність новонароджених, першорічних і другорічних кроликів відповідно:
\[\left\{\begin{array}{rrrrrrr} {}&{}&6y_{2016} &+& 8z_{2016} &=& x_{2017}\\ \frac 12x_{2016} &{}&{}&{}&{}&=& y_{2017}\\ {}&{}& \frac 12y_{2016}&{}&{}& =& z_{2017}\end{array}\right. \nonumber\]
Поширене питання: що таке асимптотична поведінка цієї системи? Як буде виглядати популяція кроликів через 100 років? Виявляється, це проблема з власним значенням.
Астероїд спостерігали в наступних місцях:
\[ (0,2),\, (2,1),\, (1,-1),\, (-1,-2),\, (-3,1),\, (-1,-1). \nonumber \]
Його орбіта навколо Сонця еліптична; вона описується рівнянням форми
\[ x^2 + By^2 + Cxy + Dx + Ey + F = 0. \nonumber \]
Яка найбільш вірогідна орбіта астероїда, враховуючи, що мала місце якась значна похибка при вимірюванні його положення? Підстановка точок даних у вищевказане рівняння дає систему
\[\begin{array}{rrrrrrrrrrrrl} (0)^2 &+& B(2)^2 &+& C(0)(2) &+& D(0) &+& E(2)&+& F&=&0 \\ (2)^2 &+& B(1)^2 &+& C(2)(1) &+& D(2) &+& E(1) &+& F&=& 0 \\ (1)^2 &+& B(-1)^2 &+& C(1)(-1) &+& D(1) &+& E(-1) &+& F&=& 0 \\ (-1)^2 &+& B(-2)^2 &+& C(-1)(-2) &+& D(-1)&+& E(-2)&+&F&=& 0 \\ (-3)^2 &+& B(1)^2 &+& C(-3)(1) &+& D(-3)&+& E(1)&+& F&=& 0 \\ (-1)^2 &+& B(-1)^2 &+& C(-1)(-1)&+& D(-1)&+& E(-1)&+&F&=&0. \end{array}\nonumber\]
Немає фактичного рішення цієї системи через похибку вимірювання, але ось найкраще підходить еліпс:
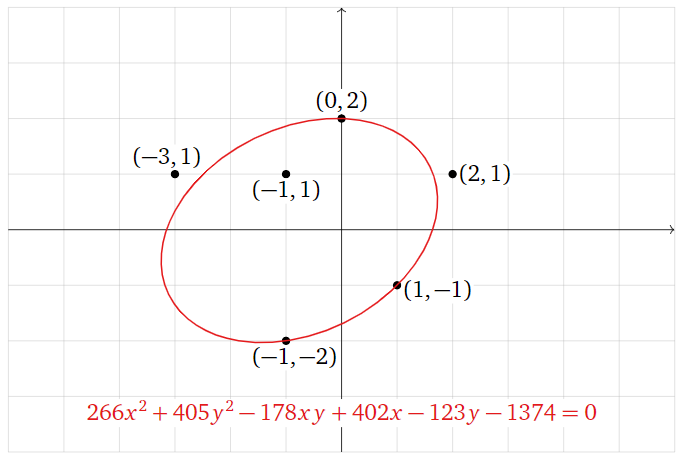
Малюнок\(\PageIndex{3}\)
Кожна веб-сторінка має певну важливість, якою вона ділиться через вихідні посилання на інші сторінки. Це призводить до мільярдів рівнянь у мільярдах змінних. Ларрі Пейдж і Сергій Брін зрозуміли, що це проблема лінійної алгебри в своїй основі, і використали розуміння, щоб знайти Google. Цей приклад ми детально розберемо в розділі 5.5. Результатом є так званий «власнийвектор на 25 мільярдів доларів». Дивіться розділ 6.6 повної версії книги для детального обговорення цього прикладу.
Як користуватися цим підручником
Існує ряд різних категорій ідей, які містяться в більшості розділів. Вони перераховані у верхній частині розділу, в розділі Цілі, для зручного перегляду. Класифікуємо їх наступним чином.
- Рецепти: це алгоритми, які, як правило, прості (якщо іноді нудні), і зазвичай виконуються комп'ютером в реальному житті. Тим не менш, їм важливо вчитися і практикувати.
- Словникові слова: формування концептуального розуміння предмета лінійної алгебри означає вміти спілкуватися набагато точніше, ніж у звичайній мові. Словникові слова мають точні визначення, які повинні бути вивчені і використані правильно.
- Основні словникові слова: ці словникові слова є важливими тим, що вони формують суть предмета лінійної алгебри. Наприклад, якщо ви не знаєте визначення власноговектора, то за визначенням ви не можете претендувати на розуміння лінійної алгебри.
- Теореми: вони точно описують, як об'єкти, що представляють інтерес, пов'язані один з одним. Знання того, який рецепт використовувати в даній ситуації, як правило, означає визнання того, які словникові слова використовувати для опису ситуації, і розуміння того, які теореми застосовуються до цієї проблеми.
- Зображення: візуалізація геометрії, що лежить в основі алгебри, означає інтерпретацію та малювання зображень задіяних об'єктів. Картинки покликані бути основною частиною матеріалу в тексті: вони не просто гарне доповнення.
Цей підручник орієнтований виключно на Math 1553 в Georgia Tech. Таким чином, він містить саме той матеріал, який викладається в цьому класі; не більше, і не менше: учні математики 1553 несуть відповідальність за розуміння всього видимого змісту. В онлайн-версії прихований додатковий матеріал (наприклад, більшість прикладів і доказів), в якому потрібно натиснути на посилання, щоб розкрити його, наприклад:
Нарешті, зауважимо, що в тексті міститься понад 140 інтерактивних демонстрацій, які були створені для ілюстрації геометрії теми. Натисніть посилання «переглянути в новому вікні», і пограйте з ними! Вам знадобиться сучасний браузер. Internet Explorer не є сучасним браузером; спробуйте Safari, Chrome або Firefox. Ось демо з розділу 6.4:
Зворотній зв'язок
Кожна сторінка онлайн-версії має посилання внизу для надання зворотного зв'язку. Це перенесе вас на сторінку проблем GitHub для цієї книги. Для доступу потрібен логін Georgia Tech.

\ tikzset {середина стрілки/.style= {postaction= {прикраса = {маркування, позначка = в позиції #1 з {\ стрілка {Stealth [масштаб = 1]}},}, прикрашати},}, rmid стрілка/.style= {прикраса = {маркування, позначка = в позиції #1 з {\ стрілка зворотна {[Stealth scale = 1]}}}, прикрасити}}, середня стрілка/.default= {0.5}, стрілка rmid/. default= {0.5},}\ begin {tikzpicture} [масштаб = 2, товстий, кожен вузл/.style= {внутрішній sep=3pt, відстань мітки = 1 мм}]\ вузол в (0,2,4) {потік трафіку (автомобілі/год)};\ точка [масштаб = 1,5] (A) при (-1,1);\ точка [масштаб = 1.5] (B) при (-1);\ точка [масштаб = 1,5] (B) в (1,1));\ точка [масштаб = 1.5] (C) в (1, -1);\ точка [масштаб = 1.5] (D) в (-1, -1);\ малювати [середню стрілку] (a.Center) до ["$x$"] (b.Center);\ малювати [середню стрілку] (b.Center) до ["$y$"] (C.Center);\ намалювати [середню стрілку] (C.Center) до ["$z$"] (D.Center);\ малювати [стрілка середини] (d.Center) до ["$w$"] (a.Center);\ малювати [стрілка rmid = .3] (a.Center)) до ["$120$"] + (-1,0);\ малювати [середню стрілку=.7] (A.Center) до ["$250$"] + (0,1);\ малювати [середню стрілку=.7] (b.Center) до ["$70$» swap] + (1,0);\ малювати [rmid стрілка = .3] (b.Center) до ["$120$» своп] + (0,1);\ малювати [rmid стрілка = .3] (C.Center) до ["$530$"] + (1,0);\ малювати [середина стрілка = .7] (C.Center) до ["$390 $"] + (0, -1);\ малювати [середина стрілка = .7] (D.Center) до ["$175 $» своп] + (-1,0);\ draw [rmid стрілка = .3] (d.Center) до ["$115 $» своп] + (0, -1);\ end {tikzpicture}