4.3: Союзи та перехрестя

Ми можемо сформувати новий набір з існуючих множин, виконавши операцію набору.

Визначення: перетин

Задано два\(A\) множини і\(B\), визначити їх перетин, щоб бути множиною

\[A \cap B = \{ x\in{\cal U} \mid x \in A \wedge x \in B \} \nonumber\]

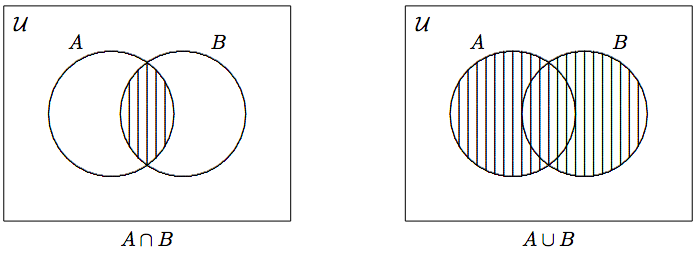
Вільно кажучи,\(A \cap B\) містить елементи, загальні для обох\(A\) і\(B\).

Визначення

Об'єднання\(A\) і\(B\) визначається як

\[A \cup B = \{ x\in{\cal U} \mid x \in A \vee x \in B \} \nonumber\]

Таким\(A \cup B\) чином, як випливає з назви, набір, що поєднує в собі всі елементи з\(A\) і\(B\).

Визначення

Встановлена різниця\(A-B\), іноді\(A \setminus B\) записувана як, визначається як

\[A- B = \{ x\in{\cal U} \mid x \in A \wedge x \not\in B \} \nonumber\]

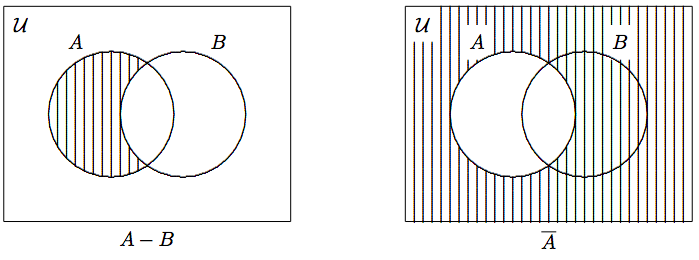
У словах\(A-B\) містить елементи, які можна знайти лише в,\(A\) але не в\(B\). Оперативно кажучи,\(A-B\) це набір,\(A\) отриманий від видалення елементів, які також належать\(B\). Тому множинну різницю ще\(A-B\) називають відносним доповненням\(B\) в\(A\). Зокрема,\({\cal U}-A\) називається доповненням\(A\), і позначається\(\overline{A}\),\(A'\) або\(A^c\).

Зауваження

Хочемо нагадати читачам, що серед авторів не рідкість приймають різні позначення для одного і того ж математичного поняття. Так само одне і те ж позначення може означати щось інше в іншому підручнику або навіть іншій галузі математики. Важливо виробити звичку вивчати контекст і переконатися, що ви розумієте сенс позначень, коли починаєте читати математичний виклад.

Приклад\(\PageIndex{1}\label{eg:unionint-01}\)

Нехай\({\cal U}=\{1,2,3,4,5\}\),\(A=\{1,2,3\}\), і\(B=\{3,4\}\). Знайти\(A\cap B\),\(A\cup B\),\(A-B\),\(B-A\),\(\overline{A}\), і\(\overline{B}\).

Рішення

У нас є\[\begin{array}{r c l} A\cap B &=& \{3\}, \\ A\cup B &=& \{1,2,3,4\}, \\ A - B &=& \{1,2\}, \\ B - A &=& \{4\}. \end{array} \nonumber\] Ми також знаходимо\(\overline{A} = \{4,5\}\), і\(\overline{B} = \{1,2,5\}\).

практичні вправи\(\PageIndex{1}\label{he:unionint-01}\)

Нехай\({\cal U} = \{\mbox{John}, \mbox{Mary}, \mbox{Dave}, \mbox{Lucy}, \mbox{Peter}, \mbox{Larry}\}\),\[A = \{\mbox{John}, \mbox{Mary}, \mbox{Dave}\}, \qquad\mbox{and}\qquad B = \{\mbox{John}, \mbox{Larry}, \mbox{Lucy}\}. \nonumber\] знайти\(A\cap B\),\(A\cup B\),,\(A-B\),\(B-A\),\(\overline{A}\), і\(\overline{B}\).

практичні вправи\(\PageIndex{2}\label{he:unionint-02}\)

\(A\subseteq B\)Якби, що б було\(A-B\)?

Приклад\(\PageIndex{2}\label{eg:unionint-02}\)

Безліч цілих чисел може бути записаний як\[\mathbb{Z} = \{-1,-2,-3,\ldots\} \cup \{0\} \cup \{1,2,3,\ldots\}. \nonumber\] Чи можемо ми\(\{0\}\) замінити на 0? Поясніть.

практичні вправи\(\PageIndex{3}\label{he:unionint-03}\)

Поясніть, чому наступні вирази синтаксично невірні.

1. \(\mathbb{Z} = \{-1,-2,-3,\ldots\} \cup \;0\; \cup \{1,2,3,\ldots\}\).
2. \(\mathbb{Z} = \ldots,-3,-2,-1 \;\cup\; 0 \;\cup\; 1,2,3,\ldots\,\)
3. \(\mathbb{Z} = \ldots,-3,-2,-1 \;+\; 0 \;+\; 1,2,3,\ldots\,\)
4. \(\mathbb{Z} = \mathbb{Z} ^- \;\cup\; 0 \;\cup\; \mathbb{Z} ^+\)

Як би ви виправили помилки в цих виразах?

Приклад\(\PageIndex{3}\label{eg:unionint-03}\)

Для будь-якого набору\(A\), що таке\(A\cap\emptyset\)\(A\cup\emptyset\),\(A-\emptyset\),\(\emptyset-A\) і\(\overline{\overline{A}}\)?

Відповідь

Зрозуміло, що\[A\cap\emptyset = \emptyset, \qquad A\cup\emptyset = A, \qquad\mbox{and}\qquad A-\emptyset = A. \nonumber\] З визначення множини різниці ми знаходимо\(\emptyset-A = \emptyset\). Нарешті,\(\overline{\overline{A}} = A\).

Приклад\(\PageIndex{4}\label{eg:unionint-04}\)

Запишіть, в інтервальних позначеннях,\([5,8)\cup(6,9]\) і\([5,8)\cap(6,9]\).

Відповідь

Відповіді є\[[5,8)\cup(6,9] = [5,9], \qquad\mbox{and}\qquad [5,8)\cap(6,9] = (6,8). \nonumber\] Вони отримані шляхом порівняння розташування двох інтервалів на дійсному числовому рядку.

практичні вправи\(\PageIndex{4}\label{he:unionint-04}\)

Запишіть, в інтервальних позначеннях,\((0,3)\cup[-1,2)\) і\((0,3)\cap[-1,2)\).

Приклад\(\PageIndex{5}\label{eg:unionint-05}\)

Тепер ми можемо описати наступний набір\[\{x\in\mathbb{R} \mid (x<5) \vee (x>7)\} \nonumber\] в інтервальних позначеннях. Він може бути написаний як\((-\infty,5)\cup(7,\infty)\) або, використовуючи комплемент,\(\mathbb{R}-[5,7\,]\). Отже, кажучи те\(x\notin[5,7\,]\) саме, що говорити\(x\in(-\infty,5) \cup(7,\infty)\), або еквівалентно\(x\in \mathbb{R}-[5,7\,]\).

Теорема\(\PageIndex{1}\label{thm:setprop}\)

Наступні властивості утримуються як для будь-яких наборів\(A\)\(B\), так і\(C\) в універсальному наборі\({\cal U}\).

1. Комутативні властивості:\(\begin{array}[t]{l} A \cup B = B \cup A, \\ A \cap B = B \cap A. \end{array}\)
2. Асоціативні властивості:\(\begin{array}[t]{l} (A \cup B) \cup C = A \cup (B \cup C), \\ (A \cap B) \cap C = A \cap (B \cap C). \end{array}\)
3. Розподільні закони:\(\begin{array}[t]{l} A \cup (B \cap C) = (A \cup B) \cap (A \cup C), \\ A \cap (B \cup C) = (A \cap B) \cup (A \cap C). \end{array}\)
4. Ідемпотентні закони:\(\begin{array}[t]{l} A \cup A = A, \\ A \cap A = A. \end{array}\)
5. Закони Де Моргана:\(\begin{array}[t]{l} \overline{A \cup B} = \overline{A} \cap \overline{B}, \\ \overline{A \cap B} = \overline{A} \cup \overline{B}. \end{array}\)
6. Закони виключеного середнього, або зворотного законів:\(\begin{array}[t]{l} A \cup \overline{A} = {\cal U}, \\ A \cap \overline{A} = \emptyset. \end{array}\)

Як ілюстрація, ми доведемо розподільний закон\[A \cup (B \cap C) = (A \cup B) \cap (A \cup C). \nonumber\] Ми повинні показати, що\[\forall x\in{\cal U}\, \big[x \in A \cup (B \cap C) \Leftrightarrow x \in (A \cup B) \cap (A \cup C) \big]. \nonumber\] еквівалентно, ми повинні показати, що Так\[A \cup (B \cap C) \subseteq (A \cup B) \cap (A \cup C), \qquad\mbox{and}\qquad (A \cup B) \cap (A \cup C) \subseteq A \cup (B \cap C). \nonumber\] чи інакше, нам потрібно встановити рівність у два кроки.

Ми зараз наводимо два докази розподільного закону\(A \cup (B \cap C) = (A \cup B) \cap (A \cup C)\).

Доказ 1

Нехай\(x\in A\cup(B\cap C)\). Потім\(x\in A\), або\(x\in B\cap C\). Ми знаємо, що\(x\in B\cap C\) означає, що\(x\in B\) і\(x\in C\). Отже, у нас є

1. \(x\in A\)або\(x\in B\), і
2. \(x\in A\)або\(x\in C\);

еквівалентно,

1. \(x\in A\cup B\), і
2. \(x\in A\cup C\).

Таким чином,\(x\in (A\cup B)\cap (A\cup C)\). Ми це довели\(A\cup(B\cap C) \subseteq (A\cup B)\cap(A\cup C)\).

Тепер давайте\(x\in (A\cup B)\cap(A\cup C)\). Потім\(x\in A\cup B\) і\(x\in A\cup C\). З визначення союзу знаходимо

1. \(x\in A\)або\(x\in B\), і
2. \(x\in A\)або\(x\in C\).

Обидві умови вимагають\(x\in A\), тому ми можемо переписати їх як

1. \(x\in A\), або
2. \(x\in B\)і\(x\in C\);

еквівалентно,

1. \(x\in A\), або
2. \(x\in B\cap C\).

Таким чином,\(x\in A\cup(B\cap C)\). Це доводить це\((A\cup B)\cap(A\cup C) \subseteq A\cup(B\cap C)\). Разом з\(A\cup(B\cap C) \subseteq (A\cup B)\cap(A\cup C)\), робимо висновок, що\(A\cup(B\cap C) = (A\cup B) \cap(A\cup C)\).

Нижче наведено альтернативний доказ. Цей тип аргументу коротший, але є більш символічним; отже, його складніше слідувати.

Доказ 2

З\[ \begin{array}{r l l} x \in A \cup (B \cap C) & \Leftrightarrow x \in A \vee x \in (B \cap C) & (\text{defn. of union}) \\ & \Leftrightarrow x \in A \vee (x \in B \wedge x \in C) & (\text{defn. of intersection}) \\ & \Leftrightarrow (x \in A \vee x \in B) \wedge (x \in A \vee x \in C) & (\text{distributive law}) \\ & \Leftrightarrow (x \in A \cup B) \wedge (x \in A \cup C) & (\text{defn. of union}) \\ & \Leftrightarrow x \in (A \cup B) \cap (A \cup B) & (\text{defn. of intersection}) \end{array} \nonumber\] цього випливає\(A \cup (B \cap C) = (A\cup B) \cap (A\cup C)\).

практичні вправи\(\PageIndex{5}\label{he:unionint-05}\)

Доведіть, що\(A\cap(B\cup C) = (A\cap B)\cup(A\cap C)\).

практичні вправи\(\PageIndex{6}\label{he:unionint-06}\)

Доведіть, що якщо\(A\subseteq B\) і\(A\subseteq C\), то\(A\subseteq B\cap C\).

Обговорення

Почнемо з чернетки. Заява, яку ми хочемо довести, має форму\[(A\subseteq B) \wedge (A\subseteq C) \Rightarrow A\subseteq B\cap C. \nonumber\] Отже, що ми припускаємо і що ми хочемо довести?

Припустимо:

Хочу довести:

Ви поставили ми припускаємо\(A\subseteq B\) і\(A\subseteq C\), і ми хочемо довести\(A\subseteq B\cap C\)? Чудово! Тепер, що це означає\(A\subseteq B\)? Як щодо\(A\subseteq C\)? У чому сенс\(A\subseteq B\cap C\)?

\(A\subseteq B\)означає: Для будь-якого\(x\in{\cal U}\), якщо\(x\in A\), то\(x\in B\) так само.

\(A\subseteq C\)означає:

\(A\subseteq B\cap C\)означає:

Як ви можете використовувати перші два фрагменти інформації, щоб отримати те, що нам потрібно встановити?

Тепер настав час зібрати все воєдино, і відшліфувати його до остаточного варіанту. Запам'ятайте три речі:

1. контур доказу,
2. причина в кожному кроці головного аргументу, і
3. вступ і висновок.

Помістіть повний доказ у простір нижче.

Ось два результати, пов'язані з доповненнями.

Теорема\(\PageIndex{1}\label{thm:subsetsbar}\)

Для будь-яких двох наборів\(A\) і\(B\), у нас є\(A \subseteq B \Leftrightarrow \overline{B} \subseteq \overline{A}\).

Теорема\(\PageIndex{1}\label{thm:genDeMor}\)

Для будь-яких наборів\(A\),\(B\) і\(C\),\[\begin{aligned} A-(B\cup C) &=& (A-B)\cap(A-C), \\ A-(B\cap C) &=& (A-B)\cup(A-C), \end{aligned} \nonumber\]

Резюме та огляд

• Запам'ятовуйте визначення перетину, об'єднання та встановлення різниці. Ми покладаємося на них, щоб довести або отримати нові результати.
• Перетин двох множин\(A\) і\(B\), позначається\(A\cap B\), являє собою сукупність елементів, загальних для обох\(A\) і\(B\). В символах,\(\forall x\in{\cal U}\,\big[x\in A\cap B \Leftrightarrow (x\in A \wedge x\in B)\big]\).
• Об'єднання двох множин\(A\) і\(B\), позначається\(A\cup B\), являє собою безліч, що поєднує в собі всі елементи в\(A\) і\(B\). В символах,\(\forall x\in{\cal U}\,\big[x\in A\cap B \Leftrightarrow (x\in A\vee x\in B)\big]\).
• Множинна різниця між двома множинами\(A\) і\(B\)\(A-B\), позначається, - це набір елементів, які можна знайти лише в,\(A\) але не в\(B\). У символі це означає\(\forall x\in{\cal U}\, \big[x\in A-B \Leftrightarrow (x\in A \wedge x\notin B)\big]\).
• Знати властивості перетину, об'єднання та набору відмінностей, перелічених у теоремі 4.3.1.

Вправа\(\PageIndex{1}\label{ex:unionint-01}\)

Запишіть кожен з наступних наборів, перерахувавши його елементи явно.

1. \([-4,4]\cap\mathbb{Z}\)
2. \((-4,4]\cap\mathbb{Z}\)
3. \((-4,\infty)\cap\mathbb{Z}\)
4. \((-\infty,4]\cap\mathbb{N}\)
5. \((-4,\infty)\cap\mathbb{Z}^-\)
6. \((4,5)\cap\mathbb{Z}\)

Вправа\(\PageIndex{2}\label{ex:unionint-02}\)

Припустимо\({\cal U} = \mathbb{Z}\), і нехай

\[ \begin{array}{c} A=\{\ldots, -6,-4,-2,0,2,4,6, \ldots \} = 2\mathbb{Z}, \\ B=\{\ldots, -9,-6,-3,0,3,6,9, \ldots \} = 3\mathbb{Z}, \\ C=\{\ldots, -12,-8,-4,0,4,8,12, \ldots \} = 4\mathbb{Z}. \end{array} \nonumber\]

Опишіть наступні набори, перерахувавши їх елементи явно.

1. \(A\cap B\)
2. \(C-A\)
3. \(A-B\)
4. \(A\cap\overline{B}\)
5. \(B-A\)
6. \(B\cup C\)
7. \((A\cup B)\cap C\)
8. \((A\cup B)-C\)

Вправа\(\PageIndex{3}\label{ex:unionint-03}\)

Ці твердження правдиві чи хибні?

• \([1,2]\cap[2,3] = \emptyset\)
• \([1,2)\cup(2,3] = [2,3]\)

Вправа\(\PageIndex{4}\label{ex:unionint-04}\)

Нехай універсальним набором\({\cal U}\) буде набір людей, які проголосували на президентських виборах в США 2012 року. Визначте\(B\) підмножини\(D\), і\(W\)\({\cal U}\) наступним чином:\[\begin{array}{r c l} D &=& \{x\in{\cal U} \mid x \mbox{ registered as a Democrat}\}, \\ B &=& \{x\in{\cal U} \mid x \mbox{ voted for Barack Obama}\}, \\ W &=& \{x\in{\cal U} \mid x \mbox{ belonged to a union}\}. \end{array} \nonumber\] Висловіть наступні\({\cal U}\) підмножини в терміні\(D\)\(B\), і\(W\).

1. Люди, які не голосували за Барака Обаму.
2. Члени профспілки, які проголосували за Барака Обаму.
3. Зареєстровані демократи, які голосували за Барака Обаму, але не належали до союзу.
4. Члени Союзу, які або не були зареєстровані як демократи, або проголосували за Барака Обаму.
5. Люди, які голосували за Барака Обаму, але не були зареєстровані як демократи і не були членами профспілки.
6. Люди, які або були зареєстровані як демократи і були членами профспілки, або не голосували за Барака Обаму.

Вправа\(\PageIndex{5}\label{ex:unionint-05}\)

Страхова компанія класифікує свій набір власників\({\cal U}\) полісів за наступними наборами:\[\begin{array}{r c l} A &=& \{x\mid x\mbox{ drives a subcompact car}\}, \\ B &=& \{x\mid x\mbox{ drives a car older than 5 years}\}, \\ C &=& \{x\mid x\mbox{ is married}\}, \\ D &=& \{x\mid x\mbox{ is over 21 years old}\}, \\ E &=& \{x\mid x\mbox{ is a male}\}. \end{array} \nonumber\] Опишіть кожну з наступних\({\cal U}\) підмножин з точки зору\(A\)\(B\),\(C\),\(D\), і\(E\).

1. Чоловічі поліси старше 21 року.
2. Власники полісів, які є жінками або керують автомобілями більше 5 років.
3. Жіночі поліси старше 21 року, які керують малогабаритними автомобілями.
4. Чоловіки-поліси, які перебувають або в шлюбі, або старше 21 року і не керують малогабаритними автомобілями.

Вправа\(\PageIndex{6}\label{ex:unionint-06}\)

\(B\)Дозволяти\(A\) і бути довільними множинами. Заповніть наступні твердження.

1. \(A\subseteq B \Leftrightarrow A\cap B = ~ \rule{3cm}{0.4pt}\).
2. \(A\subseteq B \Leftrightarrow A\cup B = ~ \rule{3cm}{0.4pt}\).
3. \(A\subseteq B \Leftrightarrow A - B = ~ \rule{3cm}{0.4pt}\).
4. \(A\subset B \Leftrightarrow (A-B=~ \rule{3cm}{0.4pt}\,\wedge\,B-A\neq~ \rule{3cm}{0.4pt}\,)\).
5. \(A\subset B \Leftrightarrow (A\cap B=~ \rule{3cm}{0.4pt}\,\wedge\,A\cap B\neq~ \rule{3cm}{0.4pt}\,)\).
6. \(A - B = B - A \Leftrightarrow ~ \rule{3cm}{0.4pt}\,\).

Вправа\(\PageIndex{7}\label{ex:unionint-07}\)

Наведіть приклади наборів\(A\) і\(B\) таких, що\(A\in B\) і\(A\subset B\).

Вправа\(\PageIndex{8}\label{ex:unionint-08}\)

Доведіть закони Де Моргана.

Вправа\(\PageIndex{9}\label{ex:unionint-09}\)

Нехай\(A\)\(B\), і\(C\) бути будь-які три набори. Доведіть, що якщо\(A\subseteq C\) і\(B\subseteq C\), то\(A\cup B\subseteq C\).

Вправа\(\PageIndex{10}\label{ex:unionint-10}\)

Довести теорему 4.3.2

Вправа\(\PageIndex{11}\label{ex:unionint-11}\)

Довести теорему 4.3.3

Вправа\(\PageIndex{12}\label{ex:unionint-12}\)

Нехай\(A\)\(B\), і\(C\) бути будь-які три набори. Доведіть, що

1. \(A-B=A\cap\overline{B}\)
2. \(A=(A-B)\cup(A\cap B)\)
3. \(A-(B-C) = A\cap(\overline{B}\cup C)\)
4. \((A-B)-C = A-(B\cup C)\)

Вправа\(\PageIndex{13}\label{ex:unionint-13}\)

Прокоментуйте наступні твердження. Вони синтаксично правильні?

1. \(x\in A \cap x\in B \equiv x\in A\cap B\)
2. \(x\in A\wedge B \Rightarrow x\in A\cap B\)

Вправа\(\PageIndex{14}\label{ex:unionint-14}\)

Довести або спростувати кожне з наступних тверджень про довільні\(A\) множини і\(B\). Якщо ви вважаєте, що твердження є істинним, доведіть його; якщо ви вважаєте, що це помилково, наведіть контрприклад.

1. \(\wp(A\cap B) = \wp(A)\cap\wp(B)\)
2. \(\wp(A\cup B) = \wp(A)\cup\wp(B)\)
3. \(\wp(A - B) = \wp(A) - \wp(B)\)

Зауваження

Щоб показати, що два\(U\) набори і\(V\) рівні, ми зазвичай хочемо довести це\(x\in U \Leftrightarrow x\in V\). У цій задачі елемент насправді\(x\) є множиною. Оскільки ми зазвичай використовуємо великі літери для позначення множин, ми повинні почати доказ (а) з «Нехай»\(S\in\wp(A\cap B)\). Якщо ви віддаєте перевагу використанню альтернативного підходу, це виглядає наступним чином:\[\begin{array}{r c l} S\in\wp(A\cap B) &\Leftrightarrow& \ldots \\ &\Leftrightarrow& \ldots \\ &\vdots& \\ &\Leftrightarrow& S\in\wp(A)\cap\wp(B). \end{array} \nonumber\] Ці зауваження також стосуються (b) та (c).