4.2: Підмножини та набори живлення

Зазвичай ми розглядаємо множини, що містять елементи схожих типів. Колекція всіх розглянутих предметів називається універсальним набором, і позначається\({\cal U}\). Наприклад, для чисел універсальний набір є\(\mathbb{R}\).

Приклад\(\PageIndex{1}\label{eg:subsets-geomfig}\)

Діаграми Венна корисні для демонстрації встановлених відносин. Нехай\[\begin{array}{c c l} {\cal U} &=& \mbox{set of geometric figures}, \\ S &=& \mbox{set of squares}, \\ P &=& \mbox{set of parallelogram}, \\ R &=& \mbox{set of rhombuses}, \\ L &=& \mbox{set of rectangles}, \\ C &=& \mbox{set of circles}. \end{array} \nonumber\] Їх зв'язок відображається на малюнку\(\PageIndex{1}\).

Малюнок\(\PageIndex{1}\): Взаємозв'язок між різними наборами геометричних фігур.

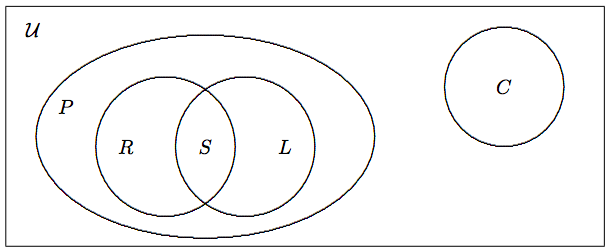
Мальовниче зображення на малюнку\(\PageIndex{1}\) називається діаграмою Венна. Ми використовуємо прямокутник для представлення універсального набору, а кола або овали для представлення множин всередині універсального набору. Відносні положення цих кіл і овалів вказують на взаємозв'язок відповідних множин. Наприклад, мати\(R\), і\(L\) всередині\(P\) означає\(S\), що ромби, квадрати і прямокутники є паралелограмами. Навпаки, кола незрівнянні з паралелограмами.

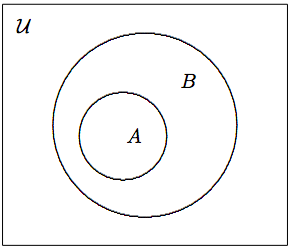
Множина\(A\) - це підмножина іншого\(B\) множини\(A \subseteq B\), позначається, якщо кожен елемент також\(A\) є елементом\(B\). Див\(\PageIndex{2}\). Малюнок. Ми також\(B\) називаємо супермножину\(A\), і пишемо\(B \supseteq A\), яка схожа на\(y\geq x\).

Малюнок\(\PageIndex{2}\): Діаграма Венна для\(A \subseteq B\).

Приклад\(\PageIndex{2}\label{eg:subsets-02}\)

Зрозуміло, що\(\mathbb{N}\subseteq\mathbb{Z}\) і\(\mathbb{Z}\subseteq\mathbb{R}\). Ми можемо вкласти ці два відносини в одне, і написати\(\mathbb{N}\subseteq\mathbb{Z} \subseteq\mathbb{R}\). Більш загально, у нас є\[\mathbb{N} \subseteq \mathbb{Z} \subseteq \mathbb{Q} \subseteq \mathbb{R}. \nonumber\] Порівняти це з\(x \leq y \leq z \leq w\). Ми виявимо багато подібності між\(\subseteq\) і\(\leq\).

Приклад\(\PageIndex{3}\label{eg:subsets-03}\)

Очевидно, що\[\{1,2,7\} \subseteq \{1,2,3,6,7,9\} \nonumber\] тому, що всі три елементи 1, 2 і 7 з набору зліва також виступають як елементи в наборі праворуч. Тим часом,\[\{1,2,7\} \nsubseteq \{1,2,3,6,8,9\} \nonumber\] тому що 7 належить до першого набору, а не другому.

Приклад\(\PageIndex{4}\label{eg:subsets-04}\)

Вірні такі твердження:

1. \(\{1,2,3\}\subseteq \mathbb{N}\).
2. \(\{x\in\mathbb{R} \mid x^2=1\} \subseteq \mathbb{Z}\).

Будьте впевнені, що ви можете чітко пояснити, чому ці зв'язки підмножини тримаються.

практичні вправи\(\PageIndex{1}\label{he:subsets-01}\)

Ці твердження правдиві чи хибні?

1. \(\{-1,2\} \nsubseteq \mathbb{N}\), і\(\{-1,2\} \subseteq \mathbb{Z}\).
2. \(\{x\in\mathbb{Z} \mid x^2\leq1\} \subseteq \mathbb{R}\).

Приклад\(\PageIndex{5}\label{eg:subsets-05}\)

Не варто вважати, що якщо\(A\nsubseteq B\) тоді ми повинні мати\(B\subseteq A\). Наприклад, якщо\(A=\{1,5,7\}\) і\(B=\{3,8\}\), то\(A \nsubseteq B\); але ми також маємо\(B \nsubseteq A\).

Останній приклад демонструє, що\(A\nsubseteq B\) це складніше, ніж просто зміна позначення підмножини, як ми робимо з нерівностями. Нам потрібно більш точне визначення співвідношення підмножини:

\[A \subseteq B \Leftrightarrow \forall x\in{\cal U} \,(x \in A \Rightarrow x \in B) \nonumber\]

Визначення\(A \subseteq B\).

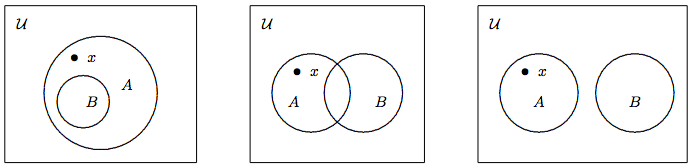
\[A \nsubseteq B \Leftrightarrow \exists x\in{\cal U} \,(x \in A \wedge x \not\in B). \nonumber\]Звідси випливає, що Отже, щоб показати, що\(A\) це не підмножина\(B\), нам потрібно знайти елемент\(x\), який належить,\(A\) але ні\(B\). Є три можливості; їх діаграми Венна зображені на малюнку\(\PageIndex{3}\).

Малюнок\(\PageIndex{3}\): Три випадки\(A \nsubseteq B\).

Приклад\(\PageIndex{6}\label{eg:subsets-06}\)

У нас є\([3,6]\subseteq[2,7)\), і\([3,6]\nsubseteq[4,7)\). У нас теж є\((3,4) \subseteq [3,4]\).

практичні вправи\(\PageIndex{2}\label{he:subsets-02}\)

Правда чи брехня:\([3,4) \subseteq (3,4)\)? Поясніть.

З поняттям універсальної множини тепер ми можемо уточнити визначення множини рівності:

\[A = B \Leftrightarrow \forall x\in{\cal U}\,(x\in A \Leftrightarrow x\in B) \nonumber\]

Логічно,\(x\in A \Leftrightarrow x\in B\) це еквівалентно\[(x\in A \Rightarrow x\in B) \wedge (x\in B\Rightarrow x\in A). \nonumber\] Тому ми також можемо визначити рівність множин за допомогою підмножини відносин:

\[A = B \Leftrightarrow (A \subseteq B) \wedge (B \subseteq A) \nonumber\]

які можна порівняти з\[x=y \Leftrightarrow (x\leq y) \wedge (y\leq x) \nonumber\] для дійсних чисел\(x\) і\(y\).

Це нове визначення множинної рівності говорить про те, що для того, щоб довести це\(A=B\), ми могли б використовувати цей двоетапний аргумент:

1. Покажіть, що\(A \subseteq B\).
2. Покажіть, що\(B \subseteq A\).

Цей прийом стане в нагоді, коли неможливо або недоцільно перерахувати елементи\(A\) і\(B\) для порівняння. Це особливо вірно, коли\(A\) і\(B\) визначаються абстрактно. Ми будемо застосовувати цю техніку в наступних розділах.

Ці два відносини\(\subseteq\) і мають багато\(\leq\) спільних властивостей. Перехідне властивість - ще один приклад.

Теорема\(\PageIndex{1}\label{thm:setstrans}\)

Нехай\(A\)\(B\), і\(C\) бути набори. Якщо\(A\subseteq B\) і\(B\subseteq C\), то\(A\subseteq C\).

Обговорення

Твердження теореми має форму імплікації. Щоб довести\(p\Rightarrow q\), ми починаємо з припущення і використовуємо його\(p\), щоб показати, що також\(q\) має бути правдою. У цьому випадку ці два кроки стають

1. Припустимо, що\(A\subseteq B\) і\(B\subseteq C\).
2. Покажіть, що\(A\subseteq C\).

Як ми можемо це довести\(A\subseteq C\)? Ми знаємо, що\(A\subseteq C\) це означає\[\forall x\in{\cal U}\,(x\in A\Rightarrow x\in C). \nonumber\] Отже, ми повинні почати з\(x\in A\), і спробувати показати це\(x\in C\) також. Як ми можемо це показати\(x\in C\)? Потрібно скористатися припущенням\(A\subseteq B\) і\(B\subseteq C\).

Доказ

Припустимо\(A\subseteq B\) і\(B\subseteq C\). Нехай\(x\in A\). Так як\(A\subseteq B\), у нас теж є\(x\in B\). Так само це\(B\subseteq C\) означає\(x\in C\). Оскільки кожен елемент\(x\) в також\(A\) є елементом\(C\), ми робимо висновок, що\(A\subseteq C\).

Доказ спирається на визначення зв'язку підмножини. Багато доказів в математиці досить прості, якщо ви знаєте основні визначення.

Приклад\(\PageIndex{7}\label{eg:subsets-07}\)

Доведіть\(x \in A \Leftrightarrow \{x\} \subseteq A\), що для будь-якого елемента\(x\in{\cal U}\)

Обговорення

Ми називаємо\(p\Leftrightarrow q\) двозастережним твердженням, оскільки воно складається з двох наслідків\(p \Rightarrow q\) і\(p\Leftarrow q\). Значить, нам потрібно довести це в два етапи:

1. Покажіть, що\(p \Rightarrow q\).
2. Покажіть, що\(q \Rightarrow p\).

Ми називаємо ці два наслідки необхідністю і достатністю біумовного твердження і позначаємо їх (\(\Rightarrow\)) і (\(\Leftarrow\)) відповідно. У цій проблемі

• (\(\Rightarrow\)) означає «\(x\in A\Rightarrow\{x\}\subseteq A\)».
• (\(\Leftarrow\)) означає «\(\{x\}\subseteq A\Rightarrow x\in A\)».

Ось як може виглядати доказ:

\[\begin{array}{c c c} (\Rightarrow) & \quad \text{ Assume } x\in A. & \qquad\ldots\qquad & \text{Therefore } x \subseteq A. \\ (\Leftarrow) & \quad \text{Assume } x \subseteq A. & \qquad\ldots\qquad & \text{ Therefore } x \in A. \end{array} \nonumber\]

Тепер приступаємо до завершення доказу.

Відповідь

(\(\Rightarrow\)) Припустимо\(x \in A\). Набір\(\{x\}\) містить лише один елемент\(x\), який також є елементом\(A\). Таким чином, кожен елемент також\(\{x\}\) є елементом\(A\). За визначенням,\(\{x\} \subseteq A\).

(\(\Leftarrow\)) Припустимо\(\{x\} \subseteq A\). Визначення відношення підмножини стверджує, що кожен елемент також\(\{x\}\) є елементом\(A\). Зокрема,\(x\) є елементом\(\{x\}\), тому він також є елементом\(A\). Таким чином,\(x \in A\).

Визначення

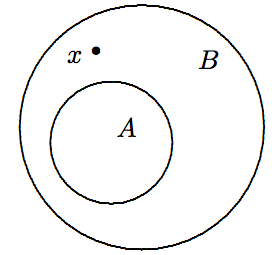
Множина\(A\) є належною підмножиною\(B\), позначається\(A \subsetneq B\) або\(A \subset B\), якщо\(A\) є підмножиною\(B\), і\(A\neq B\). Символічно,\(A \subset B \Leftrightarrow (A \subseteq B) \wedge (A \neq B)\). Аналогічно,\[A \subset B \Leftrightarrow (A \subseteq B) \wedge \exists x\in{\cal U}\,(x \in B \wedge x \not\in A). \nonumber\] див. Діаграму Венна на малюнку\(\PageIndex{4}\).

Малюнок\(\PageIndex{4}\): Визначення належної підмножини.

Приклад\(\PageIndex{8}\label{eg:subsets-08}\)

Зрозуміло, що\([0,5]\subset\mathbb{R}\). У нас також є\[\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R}. \nonumber\] Зверніть увагу на подібність між\(\subset\) і\(<\). Порівняти останній вираз з\[x < y < z < w. \nonumber\] Here - це ще одна схожість між\(\subset\) і\(<\). Для чисел,\(x<y\) і\(y<z\) разом мають на увазі, що\(x<z\). Ми називаємо це перехідним властивістю. Аналогічним чином, для наборів, якщо\(A\subset B\) і\(B\subset C\), то\(A\subset C\); див. Теорема\(4.2.1\).

практичні вправи\(\PageIndex{3}\label{he:subsets-03}\)

Правда чи брехня:\((3,4)\subset[3,4]\)? Як щодо\((3,4)\subset(3,4]\)?

Теорема\(\PageIndex{2} \label{thm:twosubsets}\)

Для будь-якого набору\(A\) у нас є\(\emptyset \subseteq A\) і\(A \subseteq A\). Зокрема,\(\emptyset\subseteq\emptyset\).

Доказ

Оскільки кожен елемент\(A\) також з'являється в\(A\), відразу випливає, що\(A\subseteq A\). Щоб показати це\(\emptyset\subseteq A\), нам потрібно перевірити підтекст\[x\in\emptyset \Rightarrow x\in A \nonumber\] для будь-якого довільного\(x\in{\cal U}\). Оскільки\(\emptyset\) порожній, завжди\(x\in\emptyset\) хибний; отже, імплікація завжди вірна. Отже,\(\emptyset\subseteq A\) для будь-якого набору\(A\). Зокрема, коли\(A=\emptyset\), отримаємо\(\emptyset\subseteq \emptyset\).

Приклад\(\PageIndex{9}\label{eg:subsets-09}\)

Визначте істинні значення цих виразів.

1. \(\emptyset \in \emptyset\)
2. \(1 \subseteq \{1\}\)
3. \(\emptyset \in \{\emptyset\}\)

Відповідь

1. За визначенням, порожній набір не містить жодного елемента. Отже, твердження\(\emptyset\in\emptyset\) є помилковим.
2. Відношення підмножини існує лише між двома множинами. Зліва від символу\(\subseteq\) у нас є тільки число, яке не є набором. Значить, твердження є помилковим. Насправді цей вислів синтаксично невірно.
3. Набір\(\{\emptyset\}\) містить один елемент, який буває порожнім набором. Порівняйте це з порожнім ящиком всередині іншого ящика. Зовнішня коробка описується парою встановлених дужок\(\{\,\ldots\,\}\), а (порожня) коробка всередині -\(\emptyset\). Звідси випливає, що\(\emptyset\in\{\emptyset\}\) є правдивим твердженням.

практичні вправи\(\PageIndex{4}\label{he:subsets-04}\)

Визначте істинні значення цих виразів.

1. \(\emptyset \subseteq \{\emptyset\}\)
2. \(\{1\} \subseteq \big\{1,\{1,2\}\big\}\)
3. \(\{1\} \subseteq \big\{\{1\},\{1,2\}\big\}\)

Визначення

Безліч всіх підмножин\(A\) називається множиною потужності\(A\), що позначається\(\wp(A)\).

Оскільки сам набір потужності є набором, нам потрібно використовувати пару лівих і правих фігурних дужок (встановити дужки), щоб укласти всі його елементи. Її елементи являють собою самі набори, для кожного з яких потрібна своя пара лівих і правих фігурних дужок. Отже, нам потрібно щонайменше два рівні встановлених дужок для опису набору потужності.

Приклад\(\PageIndex{10}\label{eg:subsets-10}\)

Нехай\(A=\{1,2\}\) і\(B=\{1\}\). \(A\)Підмножини\(\emptyset\) are\(\{1\}\),\(\{2\}\) і\(\{1,2\}\). Тому подібним\[\wp(A) = \big\{ \emptyset, \{1\}, \{2\}, \{1,2\} \big\}. \nonumber\] чином ми знаходимо\[\wp(B) = \big\{ \emptyset, \{1\} \big\}. \nonumber\] Ми можемо писати безпосередньо,\[\wp(\{1,2\}) = \big\{ \emptyset, \{1\}, \{2\}, \{1,2\} \big\}, \qquad\mbox{and}\qquad \wp(\{1\}) = \big\{ \emptyset, \{1\} \big\} \nonumber\] не вводячи листи для представлення наборів, що беруть участь.

практичні вправи\(\PageIndex{5}\label{he:subsets-05}\)

Давайте оцінимо\(\wp(\{1,2,3,4\})\). Щоб переконатися, що жодна підмножина не пропущена, ми перерахуємо ці підмножини відповідно до їх розмірів. Оскільки\(\emptyset\) є підмножиною будь-якої множини, завжди\(\emptyset\) є елементом у наборі потужності. Це підмножина розміру 0. Далі перелічіть одноелементні підмножини (підмножини з одним елементом). Потім підмножини doubleton, і так далі. Заповніть наступну таблицю.

\[\begin{array}{|c|l|} \hline \mbox{size} & \mbox{subsets} \\ \hline 0 & \emptyset \\ 1 & \{1\}, \{2\}, \ldots \qquad \\ 2 & \{1,2\}, \{1,3\}, \ldots \hskip2in \\ 3 & \{1,2,3\}, \ldots \hskip1in \\ 4 & \ldots \\ \hline \end{array} \nonumber\]Так як\(A\subseteq A\) для будь-якого набору\(A\) потужність набір\(\wp(A)\) завжди містить\(A\) сам себе. В результаті остання підмножина в списку повинна бути\(A\) сама.

Тепер ми готові зібрати їх разом, щоб сформувати набір потужності. Все, що вам потрібно, це помістити всі підмножини всередині пари великих фігурних дужок (набір потужності сам по собі набір; отже, йому потрібна пара фігурних дужок у своєму описі). Помістіть остаточну відповідь у простір нижче.

Перевірте, щоб переконатися, що ліва і права дужки ідеально збігаються.

Приклад\(\PageIndex{11}\label{eg:subsets-11}\)

Оскільки\(A\) є підмножиною\(A\), вона належить до\(\wp(A)\). Тим не менш, це неправильно сказати\(A \subseteq \wp(A)\). Чи можете ви пояснити чому? Якими повинні бути правильні позначення?

Відповідь

Набір потужності\(\wp(A)\) - це сукупність всіх підмножин\(A\). Таким чином, елементи в\(\wp(A)\) є підмножинами\(A\). Однією з таких підмножин є\(A\) сама множина. Отже,\(A\) сама з'являється як елемент в\(\wp(A)\), і ми пишемо,\(A\in\wp(A)\) щоб описати це членство.

Це відрізняється від того, щоб сказати, що\(A\subseteq\wp(A)\). Для того, щоб мати зв'язок \(A\subseteq\wp(A)\)підмножини, кожен елемент в також\(A\) повинен відображатися як елемент в\(\wp(A)\). Елементи\(\wp(A)\) є множинами (вони є підмножинами\(A\), а підмножини - множинами). Елемент не\(A\) збігається з підмножиною\(A\). Тому, хоча і\(A\subseteq\wp(A)\) синтаксично коректно, його істинне значення хибне.

практичні вправи\(\PageIndex{6}\label{he:subsets-06}\)

Поясніть різницю між\(\emptyset\) і\(\{\emptyset\}\). Скільки елементів є в\(\emptyset\) і\(\{\emptyset\}\)? Це правда\(\wp(\emptyset) = \{\emptyset\}\)?

Теорема\(\PageIndex{3}\label{thm:powersetcard}\)

Якщо\(A\) набір\(n\) -element, то\(\wp(A)\) має\(2^n\) елементи. Іншими словами, набір\(n\) -element має\(2^n\) різні підмножини.

Доказ

Скільки підмножин ми\(A\) можемо побудувати? Щоб сформувати підмножину, ми проходимо кожен з\(n\) елементів і запитуємо себе, чи хочемо ми включити цей конкретний елемент чи ні. Оскільки існує два варіанти (так чи ні) для кожного з\(n\) елементів у\(A\), ми знайшли\(\underbrace{2\cdot2\cdot\cdots2}_{\mbox{n times}}\, =2^n\) підмножини.

практичні вправи\(\PageIndex{7}\label{he:subsets-07}\)

Скільки елементів є в\(\wp(\{\alpha,\beta, \gamma\})\)? Які вони?

практичні вправи\(\PageIndex{8}\label{he:subsets-08}\)

У чому полягає кардинальність\(\emptyset\)? Як щодо\(\wp(\emptyset)\)? Опишіть\(\wp(\emptyset)\).

практичні вправи\(\PageIndex{9}\label{he:subsets-09}\)

Чи правильно писати\(|\wp(A)|=2^{|A|}\)? Як щодо\(|\wp(A)|=2^A\)? Поясніть.

Приклад\(\PageIndex{12}\label{eg:subsets-12}\)

Коли набір містить набори як елементи, його набір потужності може стати досить складним. Ось два приклади. \[\begin{aligned} \wp(\big\{\{ a\},\{1\}\big\}) &=& \Big\{ \emptyset, \big\{\{a\}\big\}, \big\{\{1\}\big\}, \big\{\{a\},\{1\}\big\} \Big\}, \\ \wp(\big\{\emptyset,\{1\}\big\}) &=& \Big\{ \emptyset, \{\emptyset\}, \big\{\{1\}\big\}, \big\{\emptyset,\{1\}\big\} \Big\}. \end{aligned} \nonumber\]Переконайтеся, що ви розумієте позначення, використовувані в цих прикладах. Зокрема, вивчіть кількість рівнів встановлених дужок, які використовуються в кожному прикладі.

Резюме та огляд

• Множина\(S\) є підмножиною іншого\(T\) множини тоді і тільки тоді, коли кожен елемент в\(S\) можна знайти в\(T\).
• В символах,\(S\subseteq T \Leftrightarrow \forall x\in{\cal U}\, (x\in S \Rightarrow x\in T)\).
• Отже, щоб показати\(S\subseteq T\), що, ми повинні почати з довільного елемента\(x\) в\(S\), і показати, що\(x\) також належить\(T\).
• Визначення відношення підмножини має на увазі, що для будь-якої\(S\) множини у нас завжди є\(\emptyset\subseteq S\) і\(S\subseteq S\).
• Потужність множини\(S\), що позначається\(\wp(S)\), містить всі підмножини\(S\).
• Якщо\(|S|=n\), то\(|\wp(S)|=2^n\). Отже, набір\(n\) -element має\(2^n\) підмножини.
• Для побудови\(\wp(S)\) перерахуйте підмножини\(S\) відповідно до їх розмірів. Обов'язково використовуйте пару фігурних дужок для кожної підмножини та вкладіть усі їх у пару зовнішніх фігурних дужок.

Вправи 4.2

Вправа\(\PageIndex{1}\label{ex:subsets-01}\)

Визначте, які з наведених нижче тверджень є істинними, а які - помилковими.

1. \(\{1,2,3\} \subseteq \{0,1,2,3,4\}\)
2. \(\{1,2,3\} \subseteq \mathbb{N}\)
3. \(\{1,2\} \subset [1,2]\)
4. \([2,4] \subseteq (0,6)\)
5. \([2,4) \subset [2,4]\)
6. \([2,4) \subseteq (2,4]\)

Вправа\(\PageIndex{2}\label{ex:subsets-02}\)

Визначте, які з наведених нижче тверджень є істинними, а які - помилковими.

1. \(a \subseteq \{a\}\)
2. \(\{a\} \subseteq \{a,b\}\)
3. \(\emptyset \subseteq \emptyset\)
4. \(\emptyset \subseteq \{\emptyset\}\)
5. \(\emptyset \subset \{\emptyset\}\)
6. \(\{a\} \subseteq \wp(\{\{a\},\{b\}\})\)

Вправа\(\PageIndex{3}\label{ex:subsets-03}\)

Поясніть, чому\(\mathbb{Z} \subseteq \mathbb{Q}\). Зокрема, пояснити, як виражати ціле число як раціональне число.

Вправа\(\PageIndex{4}\label{ex:subsets-04}\)

Правда чи брехня:\(\mathbb{N} \subseteq 6\mathbb{N}\)? Поясніть.

Вправа\(\PageIndex{5}\label{ex:subsets-05}\)

Якщо\(A\subseteq B\)\(B\subseteq C\), і\(C\subseteq D\), це правда\(A\subseteq D\)? Як ви називаєте цю властивість?

Вправа\(\PageIndex{6}\label{ex:subsets-06}\)

Визначте, чи є такі твердження істинними чи хибними:

1. Порожній набір\(\emptyset\) є підмножиною\(\{1,2,3\}\).
2. Якщо\(A=\{1,2,3\}\), то\(\{1\}\) є підмножиною\(\wp(A)\).

Вправа\(\PageIndex{7}\label{ex:subsets-07}\)

Знайдіть набір потужності наступних наборів.

1. \(\{a,b\}\)
2. \(\{4,7\}\)
3. \(\{x,y,z,w\}\)
4. \(\big\{\{a\}\big\}\)
5. \(\big\{ a,\{b\} \big\}\)
6. \(\big\{ \{x\},\{y\} \big\}\)

Вправа\(\PageIndex{8}\label{ex:subsets-08}\)

Оцініть наступні набори.

1. \(\wp(\{\emptyset\})\)
2. \(\wp(\wp(\{a,b\}))\)
3. \(\wp(\wp(\wp(\emptyset)))\)

Вправа\(\PageIndex{9}\label{ex:subsets-09}\)

Ми дізналися, що\(A\subseteq A\) для будь-якого набору\(A\). Тоді ми повинні писати\(A\in\wp(A)\) чи\(A\subseteq\wp(A)\)? Поясніть.

Вправа\(\PageIndex{10}\label{ex:subsets-10}\)

Доведіть, що\(X\in\wp(A)\) якщо і тільки якщо\(X\subseteq A\).

Вправа\(\PageIndex{11}\label{ex:subsets-11}\)

Визначте, які з наведених нижче тверджень є істинними, а які - помилковими. Поясніть!

1. \(\{a\}\in \{a,b,c\}\)
2. \(\{a\}\subseteq\{\{a\},b,c\}\)
3. \(\{a\}\in \wp(\{\{a\},b,c\})\)

Вправа\(\PageIndex{12}\label{ex:subsets-12}\)

Визначте, які з наведених нижче тверджень є істинними, а які - помилковими. Поясніть!

1. \(\{a\}\subseteq\{a,b,c\}\)
2. \(\{a\}\subseteq\{\{a,b\},c\}\)
3. \(\{a\}\subseteq\wp(\{\{a\},b,c\})\)