4.1: Вступ до наборів

Last updated
Save as PDF

Page ID: 64156

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Набір - це сукупність предметів. Об'єкти в наборі називаються його елементами або членами. Елементи в наборі можуть бути будь-якими типами об'єктів, включаючи набори! Члени набору навіть не обов'язково повинні бути однотипними. Наприклад, хоча він може і не мати ніякого значущого застосування, набір може складатися з цифр і імен.

Зазвичай ми використовуємо великі літери, такі як$A$$B$,$C$,$S$, і$T$ для представлення множин, і позначаємо їх загальні елементи відповідними малими літерами$a$$b$,$c$,$s$, і$t$, відповідно. Щоб вказати, що$b$ є елементом$B$ множини, ми приймаємо позначення$b\in B$, що означає «$b$належить$B$» або «$b$є елементом»$B$. Ми також пишемо$B\mathbb{N}i b$, і говоримо «$B$містить$b$ (як елемент)».

Ми позначаємо ці позначення для деяких спеціальних наборів чисел:\[\begin{array}{c c l} \mathbb{R} &=& \mbox{the set of real numbers}, \\ \mathbb{Q} &=& \mbox{the set of rational numbers}, \\ \mathbb{Z} &=& \mbox{the set of integers}, \\ \mathbb{N} &=& \mbox{the set of natural numbers (positive integers)}. \end{array} \nonumber\] Всі вони є нескінченними множинами, тому що всі вони містять нескінченно багато елементів. На відміну від цього, кінцеві множини містять скінченно багато елементів.

Ми можемо використовувати метод реєстру для опису набору, якщо він має лише невелику кількість елементів. Ми перераховуємо всі його елементи явно, як у\[A = \mbox{the set of natural numbers not exceeding 7} = \{1,2,3,4,5,6,7\}. \nonumber\] For sets з більшою кількістю елементів, показуємо перші кілька записів, щоб відобразити шаблон, і використаємо крапку, щоб вказати «і так далі». Наприклад,\[\{1,2,3,\ldots,20\} \nonumber\] представляє множину перших 20 натуральних чисел. Повторюваний візерунок може бути продовжений на невизначений час, як у\[\begin{array}{c c l} \mathbb{N} &=& \{1,2,3,\ldots\} \\ \mathbb{Z} &=& \{\ldots,-2,-1,0,1,2,\ldots\} \end{array} \nonumber\] Існує три види цілих чисел: додатне, від'ємне і беззнакове ціле число нуль. Що стосується парності, ціле число є парним або непарним. Ціле число є парним, якщо і тільки якщо воно ділиться на два. Тому множина парних цілих чисел може бути описана як$\{\ldots,-4,-2,0,2,4,\ldots\}$.

Ми можемо використовувати позначення set-builder для опису множини. Наприклад, набір натуральних чисел визначається як\[\mathbb{N} = \{x\in\mathbb{Z} \mid x>0 \}. \nonumber\] Тут, вертикальна смуга$\mid$ читається як «такий, що» або «для чого». Отже, права частина рівняння вимовляється як «множина$x$ належності до множини цілих чисел, таких що»$x>0$, або просто «множина цілих чисел$x$ такі, що»$x>0$. В цілому цей описовий метод з'являється в форматі\[\{\,\mbox{membership}\;\mid\;\mbox{properties}\,\}. \nonumber\] Позначення$\mid$ означає «такий, що» або «для чого» тільки тоді, коли він використовується в заданих позначеннях. Це може означати щось інше в іншому контексті. Тому не пишіть «нехай$x$ буде дійсним числом$\mid$$x^2>3$», якщо ви хочете сказати «нехай$x$ буде дійсне число таке, що»$x^2>3$. Вважається неправильним використання математичного позначення в якості абревіатури.

Приклад$\PageIndex{1}\label{eg:setintro-01}$

Запишіть ці два набори\[\{x\in\mathbb{Z} \mid x^2 \leq 1\} \quad\mbox{and}\quad \{x\in\mathbb{N} \mid x^2 \leq 1\} \nonumber\], перерахувавши їх елементи явно.

Відповідь: Перший набір має три елементи, і дорівнює$\{-1,0,1\}$. Другий набір - одноелементний набір; він дорівнює$\{1\}$.

практичні вправи$\PageIndex{1}\label{he:setintro-01}$

Використовуйте метод реєстру для опису наборів$\{x\in\mathbb{Z} \mid x^2\leq20\}$ і$\{x\in\mathbb{N} \mid x^2\leq20\}$.

практичні вправи$\PageIndex{2}\label{he:setintro-02}$

Використовуйте метод реєстру для опису множини\[\{x\in\mathbb{N} \mid x\leq20 \mbox{ and $x=n^2$ for some integer $n$}\}. \nonumber\]

Існує дещо інший формат позначення set-builder. Перед вертикальною смугою описуємо форму, яку припускають елементи, а після вертикальної смуги вказуємо, звідки ми збираємося підбирати ці елементи:\[\{\,\mbox{pattern}\;\mid\;\mbox{membership}\,\}. \nonumber\] Тут вертикальна смуга$\mid$ означає «де». Наприклад,\[\{ x^2 \mid x\in\mathbb{Z} \} \nonumber\] це набір$x^2$ де$x\in\mathbb{Z}$. Він являє собою набір квадратів:$\{0,1,4,9,16,25,\ldots\}$.

Приклад$\PageIndex{2}\label{eg:setintro-02}$

Набір\[\{ 2n \mid n\in\mathbb{Z} \} \nonumber\] описує набір парних чисел. Ми також можемо записати набір як$2\mathbb{Z}$.

практичні вправи$\PageIndex{3}\label{he:setintro-03}$

$\{2n+1 \mid n\in\mathbb{Z}\}$Опишіть набір методом реєстру.

практичні вправи$\PageIndex{4}\label{he:setintro-04}$

Використовуйте метод реєстру для опису набору$\{3n \mid n\in\mathbb{Z}\}$.

Інтервал - це набір дійсних чисел, всі з яких лежать між двома дійсними числами. Якщо кінцеві точки будуть включені або виключені, залежить від того, чи є інтервал відкритий, закритий або напіввідкритий. Для їх опису ми приймаємо такі інтервальні позначення:\[\displaylines{ (a,b) = \{x\in\mathbb{R} \mid a < x < b \}, \cr [a,b] = \{x\in\mathbb{R} \mid a\leq x\leq b \}, \cr [a,b) = \{x\in\mathbb{R} \mid a\leq x < b \}, \cr (a,b] = \{x\in\mathbb{R} \mid a < x\leq b \}. \cr} \nonumber\] Мається на увазі, що$a$ повинно бути менше або дорівнює$b$. Значить, позначення$(5,3)$ не має особливого сенсу. Як щодо$[3,3]$? Це законне позначення?

Інтервал містить не просто цілі числа, а всі числа між двома кінцевими точками. Під числами ми маємо на увазі цілі числа і десяткові числа. Наприклад,$(1,5) \neq \{2,3,4\}$ тому що інтервал$(1,5)$ також включає десяткові числа, такі в$1.276$$\sqrt{2}$, і$\pi$.

Ми можемо використовувати$\pm\infty$ в інтервальному позначенні:\[\begin{array}{r c l} (a,\infty) &=& \{ x\in\mathbb{R} \mid a<x \}, \\ (-\infty,a) &=& \{ x\in\mathbb{R} \mid x<a \}. \end{array} \nonumber\] Однак ми не можемо писати$(a,\infty]$ або$[-\infty,a)$, тому що$\pm\infty$ це не числа. Це нісенітниця сказати$x\leq\infty$ чи$-\infty\leq x$. З цієї ж причини ми можемо написати$[a,\infty)$ і$(-\infty,a]$, але ні$[a,\infty]$ або$[-\infty,a]$.

Приклад$\PageIndex{3}\label{eg:setintro-03}$

Пишіть інтервали$(2,3)$$[2,3]$, причому$(2,3]$ в описовій формі.

Рішення: Згідно з визначенням інтервалу, ми знаходимо\[\begin{array}{c c l} {(2,3)} &=& \{x\in\mathbb{R} \mid 2<x<3\}, \\ {[2,3]} &=& \{x\in\mathbb{R} \mid 2\leq x\leq 3\}, \\ {(2,3]} &=& \{x\in\mathbb{R} \mid 2 < x\leq 3\}. \end{array} \nonumber\] Що б ви сказали про$[2,3)$?

Приклад$\PageIndex{4}\label{eg:setintro-04}$

Запишіть ці\[\{x\in\mathbb{R} \mid -2 \leq x < 5\} \quad\mbox{and}\quad \{x\in\mathbb{R} \mid x^2 \leq 1\} \nonumber\] множини у вигляді інтервалу.

Рішення: $[-2,5)$Відповіді є і$[-1,1]$, відповідно. Членство$x$ впливає на відповіді. Якщо ми змінимо другий набір на$\{x\in\mathbb{Z} \mid x^2\leq 1\}$, відповідь була б$\{-1,0,1\}$. Чи можете ви пояснити чому$\{-1,0,1\} \neq [-1,1]$?

Приклад$\PageIndex{5}\label{eg:setintro-05}$

Переконайтеся, що ви використовуєте правильні типи чисел. Порівняйте ці два\[\begin{array}{c c l} S &=& \{x\in\mathbb{Z} \mid x^2 \leq 5 \}, \\ T &=& \{x\in\mathbb{R} \mid x^2 \leq 5 \}. \end{array} \nonumber\] множини Один складається тільки з цілих чисел, а інший містить дійсні числа. Таким чином$S=\{-2,-1,0,1,2\}$, і$T=\big[-\sqrt{5},\sqrt{5}\,\big]$.

практичні вправи$\PageIndex{5}\label{he:setintro-05}$

Які з наведених множин\[\{x\in\mathbb{Z} \mid 1<x<7\} \quad\mbox{and}\quad \{x\in\mathbb{R} \mid 1<x<7\} \nonumber\] можуть бути представлені інтервальними позначеннями$(1,7)$? Поясніть.

практичні вправи$\PageIndex{6}\label{he:setintro-06}$

Поясніть чому$[2,7\,] \neq\{2,3,4,5,6,7\}$.

практичні вправи$\PageIndex{7}\label{he:setintro-07}$

Правда чи брехня:$(-2,3)=\{-1,0,1,2\}$? Поясніть.

$S$Дозволяти бути набір чисел; ми визначаємо\[\begin{array}{c c l} S^+ &=& \{ x\in S \mid x>0 \}, \\ S^- &=& \{ x\in S \mid x<0 \}, \\ S^* &=& \{ x\in S \mid x \neq 0 \}. \end{array} \nonumber\] In plain English,$S^+$ є підмножиною$S$ містить тільки ті елементи, які є позитивними,$S^-$ містить тільки негативні елементи$S$, і$S^*$ містить тільки ненульові елементи$S$.

Приклад$\PageIndex{6}\label{eg:setintro-06}$

Це повинно бути очевидно, що$\mathbb{N}=\mathbb{Z}^+$.

практичні вправи$\PageIndex{8}\label{he:setintro-08}$

Що таке позначення множини від'ємних цілих чисел?

Деякі математики також приймають ці позначення:\[\begin{aligned} bS &=& \{ bx \mid x\in S \}, \\ a+bS &=& \{ a+bx \mid x\in S \}. \end{aligned} \nonumber\] Відповідно, ми можемо записати безліч парних цілих чисел як$2\mathbb{Z}$, а набір непарних цілих чисел може бути представлений$1+2\mathbb{Z}$.

Порожній набір - це набір, який не містить жодного елемента. Обидва\[\{x\in\mathbb{R} \mid x>0 \mbox{ and } x<0\} \qquad\mbox{and}\qquad \{x\in\mathbb{R} \mid x^2 < 0\} \nonumber\] є прикладами порожніх наборів. Другий приклад ілюструє типове застосування порожнього набору. Це забезпечує зручний спосіб заявити, що проблема не має рішення: ми говоримо, що набір рішень є порожнім набором. Позначимо порожній набір з позначенням$\emptyset$ або$\{\,\}$. Наприклад, чи можете ви пояснити чому$(3,3)=\emptyset$?

практичні вправи$\PageIndex{9}\label{he:setintro-09}$

Що$[7,7\,]$ означають позначення? Як би ви описали$(7,7\,]$ набори$(7,7)$, і$[7,7)$?

Приклад$\PageIndex{7}\label{eg:setintro-07}$

Визначте, яке з цих тверджень вірно. \[\begin{aligned} \{x\in\mathbb{R} \mid (x^2+2)(x^2+3) = 0\} &=& \emptyset, \\ \{x\in\mathbb{Z} \mid (x^2-2)(x^2+3) = 0\} &=& \emptyset, \\ \{x\in\mathbb{R} \mid (x^2-2)(x^2+3) = 0\} &=& \emptyset, \\ \{x\in\mathbb{R} \mid (x^2-2)(x^2+3)\geq0\} &=& \emptyset. \end{aligned} \nonumber\]

Рішення: Відповіді такі: істинний, істинний, хибний і хибний відповідно.

Приклад$\PageIndex{8}\label{eg:setintro-08}$

Коли ми пишемо$3,4,5,\ldots,n$, ми маємо на увазі список цілих чисел між 3 і$n$ включно. Мається на увазі, що$n\geq3$. Отже, набір\[\{3,4,5,\ldots,n\} \nonumber\] порожній, коли$n=2$.

Два$A$$B$ множини і вважаються рівними, якщо вони містять однакову колекцію елементів. Більш суворо, ми визначаємо\[A = B \Leftrightarrow \forall x \, (x \in A \Leftrightarrow x \in B). \nonumber\] Оскільки елементи множини можуть самі бути множинами, проявляйте обережність і використовуйте правильні позначення, коли ви порівнюєте вміст двох наборів.

Приклад$\PageIndex{9}\label{eg:setintro-09}$

Поясніть чому$\big\{0,\{1\}\big\} \neq \{0,1\}$.

Рішення

Множина$\big\{0,\{1\}\big\}$ складається з двох елементів: цілого числа$0$ і множини$\{1\}$. Множина$\{0,1\}$ також складається з двох елементів, обидва з яких цілих чисел; а саме 0 та 1.

Вам може знадобитися наступна аналогія. Уявіть собі, що набір є коробкою. Ви відкриваєте вікно, щоб подивитися на його вміст. Саму коробку можна порівняти з фігурними дужками$\{$ і$\}$. Те, що він тримає, - це саме те, що ми називаємо елементами набору, який він представляє. Вміст двох наборів$\big\{0,\{1\}\big\}$ і$\{0,1\}$ зображені в коробках, показаних на рис$\PageIndex{1}$.

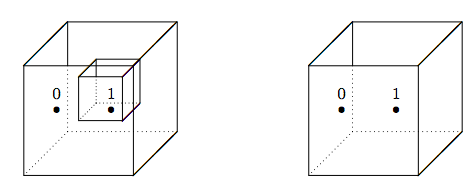
Знімок екрана 2020-01-06 в 2.54.04 PM.png — Малюнок$\PageIndex{1}$: Два$\big\{0,\{1\}\big\}$ набори і${0,1}$.

Коли ви відкриєте перший ящик, ви знайдете два предмети. Один з них - це число 0; інший - ще один ящик, який містить число 1. Друге поле також містить два пункти, які є обома числами. Те, що ви знайдете в цих двох коробках, не однакове. Отже, набори, які вони представляють, різні.

практичні вправи$\PageIndex{10}\label{he:setintro-10}$

Назвіть деякі відмінності між множинами$\big\{0,\{1\}\big\}$ і$\big\{\{0\},\{1\}\big\}$.

Приклад$\PageIndex{10}\label{eg:setintro-10}$

Правда чи брехня:$\mathbb{Z}=\big\{\{\ldots,-3,-2,-1\},0,\{1,2,3,\ldots\}\big\}$?

Рішення

Набір зліва є$\mathbb{Z}$, і\[\mathbb{Z} = \{\ldots,-3,-2,-1,0,1,2,3,\ldots\}. \nonumber\] Це нескінченний набір. Набір праворуч складається всього з трьох елементів:

множина$\{\ldots,-3,-2,-1\}$, яка є множиною від'ємних цілих чисел,
ціле число 0, і
множина$\{1,2,3,\ldots\}$, яка є множиною натуральних чисел.

Значить, їм немає рівних. Зверніть увагу, що\[\mathbb{Z} \neq \big\{\{\ldots,-3,-2,-1\}, \{0\}, \{1,2,3,\ldots\}\big\} \nonumber\] або, тому що набір праворуч - це набір з трьох наборів, тоді як набір ліворуч є набором цілих чисел. Один має три елементи; інший має нескінченно багато елементів.

Щоб зменшити плутанину, замість того, щоб говорити набір наборів, ми могли б сказати колекцію наборів або сімейство наборів. Наприклад,\[\big\{\{1,3,5,\ldots,\}, \{2,4,6,\ldots\,\}\big\} \nonumber\] це сімейство з двох множин, одна з яких є множиною натуральних непарних чисел; інша - множина позитивних парних чисел.

Визначення

Безліч вважається кінцевим, якщо він має кінцеву кількість елементів. Кількість елементів в скінченній множині$A$ називається його кардинальністю, і позначається$|A|$. Отже,$|A|$ завжди ненегативний. Якщо$A$ нескінченний набір, деякі автори пишуть$|A|=\infty$.

Приклад$\PageIndex{11}\label{eg:setintro-11}$

Хоча це банально$|\{1,4,7,8\}| = 4$, і$|\{0,1\}| = 2$, може бути не очевидно, що\[\big|\big\{0,\{1\}\big\}\big| = 2, \nonumber\] і\[\big|\big\{\{\ldots,-3,-2,-1\},0,\{1,2,3,\ldots\,\}\big\}| = 3. \nonumber\] Що важливо кількість записів у наборі, яке можна порівняти з тим, скільки предметів ви можете знайти, коли ви відкриваєте коробку. Ось ще один приклад:\[|\{x\in\mathbb{R} \mid x^2=9\}| = 2 \nonumber\] тому що рівняння$x^2=9$ має два реальних рішення. Що таке$|\{x\in\mathbb{N} \mid x^2=9\}|$?

практичні вправи$\PageIndex{11}\label{he:setintro-11}$

Визначте ці кардинальності:

$|\{x\in\mathbb{Z} \mid x^2-7x-6=0\}|$
$|\{x\in\mathbb{R} \mid x^2-x-12<0\}|$
$|\{x\in\mathbb{Z} \mid \mbox{ x is prime and x is even}\}|$

Нагадаємо, що ваші відповіді повинні бути ненегативними.

практичні вправи$\PageIndex{12}\label{he:setintro-12}$

Закриваємо цей розділ важливим зауваженням про набори. З визначення рівності множин випливає, що повторювані елементи ми не вважаємо окремими елементами. Наприклад, припустимо, невеликий студентський клуб має трьох офіцерів:

стілець:	Мері,
заступник голови:	Джон,
секретар:	Джон;

і нехай$A$ представляють сукупність її посадових осіб, і$B$ сукупність посад в її виконавчій раді, то$|A|=2$ і$|B|=3$, тому що\[A = \{ \mbox{Mary}, \mbox{John} \}, \nonumber\] і\[B = \{ \mbox{chair}, \mbox{vice chair}, \mbox{secretary}\}. \nonumber\]

Приклад$\PageIndex{12}\label{eg:setintro-12}$

Знайдіть помилки в наступному твердженні:\[|\{-2,2\}| = \{\,|-2|,|2|\} = \{2\} = 2, \nonumber\] і виправте їх.

Рішення

Це твердження містить кілька помилок. Перша помилка полягає в тому, що ми можемо розподілити символи «абсолютного значення»$|\quad|$ над вмістом набору:\[|\{-2,2\}| \neq \{\,|-2|,|2|\}. \nonumber\] Зрештою, дві вертикальні смуги в цьому випадку не означають абсолютного значення. Замість цього мається на увазі кардинальність набору$\{-2,2\}$. Отже,$|\{-2,2\}|=2$.

Друге$\{\,|-2|,|2|\} = \{2\}$ рівність правильне. Після прийняття абсолютних значень обидві записи стають 2. Однак ми не пишемо$\{|-2|,|2|\} = \{2,2\}$, тому що набір не повинен містити повторення. Тому правильно сказати$\{\,|-2|,|2|\} = \{2\}$.

Останнє рівність$\{2\}=2$ неправильне. Ми не можемо порівняти набір з числом. Уявіть собі набір$\{2\}$ як поле, що містить лише один об'єкт, і цей об'єкт є числом 2. На відміну від цього, 2 з правого боку залишаються на відкритому повітрі без будь-якого стримування. Зрозуміло, що$\{2\} \neq 2$.

Вся заява містить кілька помилок; деякі з них є синтаксичними помилками, а деякі є концептуальними. Тим не менш, у нас є$|\{-2,2\}|=2$. Хоча остаточна відповідь правильна, аргумент, який використовується для її отримання, не є.

У деяких ситуаціях ми хочемо вважати повторювані елементи як окремі елементи, як в$S=\{1,2,2,2,3,3,4,4\}$. Називаємо таку колекцію мультісетом замість звичайного набору. В даному випадку,$|S|=8$.

Резюме та огляд

Набір - це сукупність предметів (без повторів).
Щоб описати множину, або перерахуйте всі його елементи явно, або скористайтеся описовим методом.
Інтервали - це множини дійсних чисел.
Елементи в множині можуть бути будь-яким типом об'єкта, включаючи множини.
Ми навіть можемо мати набір, що містить різнорідні елементи. Зокрема, ми можемо змішувати елементи та набори всередині набору.
Якщо множина$A$ скінченна, його кардинальність$|A|$ - це кількість елементів, які вона містить. Отже,$|A|$ завжди ненегативний.

Вправи 4.1

Вправа$\PageIndex{1}\label{ex:setintro-01}$

Запишіть кожен з цих наборів, перерахувавши його елементи явно (тобто використовуючи метод реєстру).

$\{n\in\mathbb{Z} \mid -6<n<4\}$
$\{n\in\mathbb{N} \mid -6<n<4\}$
$\{x\in\mathbb{Q} \mid x^3-x^2-6x=0\}$
$\{x\in\mathbb{Q} \mid x^4-11x^2+18=0\}$.

Вправа$\PageIndex{2}\label{ex:setintro-02}$

Використовуйте метод реєстру для опису цих наборів:

$\{x\in\mathbb{N} \mid \mbox{ x<20 and x is a multiple of 3 }\}$
$\{x\in\mathbb{Z} \mid \mbox{ |x|<20 and x is a multiple of 3 or a multiple of 5 }\}$
$\{x\in\mathbb{Z} \mid \mbox{ |x|<20 and x is a multiple of 3 and a multiple of 5}\}$
$\{x\in\mathbb{N} \mid \mbox{ x<20 and x is a multiple of 3 but not a multiple of 5}\}$

Вправа$\PageIndex{3}\label{ex:setintro-03}$

Запишіть кожен з наступних множин у вигляді$\{n\in\mathbb{Z} \mid p(n)\}$ з логічним твердженням,$p(n)$ що описує властивість$n$.

$\{\ldots,-3,-2,-1\}$
$\{\ldots,-27,-8,-1,0,1,8,27,\ldots\}$
$\{0,1,4,9,16,\ldots\}$
$\{\ldots,-15,-10,-5,0,5,10,15,\ldots\}$
$\{0,4,8,12,\ldots\}$
$\{\ldots,-14,-8,-2,4,10,16,\ldots\}$

Вправа$\PageIndex{4}\label{ex:setintro-04}$

Повторіть попередню задачу, але запишіть множини у вигляді$\{ f(n) \mid n\in S\}$, де$f(n)$ знаходиться формула, яка описує візерунок елементів, і$S$ є відповідним набором чисел.

Вправа$\PageIndex{5}\label{ex:setintro-05}$

Коли це можливо, висловіть набори в Задачі 3 у вигляді$S^+$$S^-$$bS$, або$a+bS$ для якогось відповідного набору$S$.

Вправа$\PageIndex{6}\label{ex:setintro-06}$

Визначте, чи є наступні множини порожніми, кінцевими множинами або нескінченними множинами:

$\{2n+1 \mid n\in\mathbb{N}\}$
$\{x\in\mathbb{R} \mid x^2<0\}$
$\{x\in\mathbb{Q} \mid x\geq0 \mbox{ and } x\leq0\}$
$\{x\in\mathbb{N} \mid x<0 \mbox{ or } x>0\}$

Вправа$\PageIndex{7}\label{ex:setintro-07}$

Запишіть кожен з цих множин в інтервальне позначення.

$\{x\in\mathbb{R} \mid -4<x<7\}$
$\{x\in\mathbb{R} \mid -4<x\leq7\}$
$\{x\in\mathbb{R}^+\mid -4<x\leq7\}$
$\{x\in\mathbb{R} \mid -4<x\}$
$\{x\in\mathbb{R} \mid x\leq6\}$
$\{x\in\mathbb{R}^-\mid 0\leq x\leq6\}$

Вправа$\PageIndex{8}\label{ex:setintro-08}$

Чи є$[-\infty,\infty]$ законним або правильним позначенням? Поясніть.

Вправа$\PageIndex{9}\label{ex:setintro-09}$

Оцініть наступні вирази.

$|\{x\in\mathbb{Z} \mid -4<x<7\}|$
$|\{x\in\mathbb{Z} \mid -4<x\leq7\}|$
$|\{x\in\mathbb{N} \mid -4<x\leq7\}|$
$|\{x\in\mathbb{R} \mid x^4-2x^3-35x^2=0\}|$
$|\{-3,-2,2,3\}|$
$|\{x\in\mathbb{Q} \mid x^2=3\}|$

Вправа$\PageIndex{10}\label{ex:setintro-10}$

Визначте, які з наведених нижче тверджень є істинними, а які - помилковими.

$a\in\{a\}$
$\{3,5\}=\{5,3\}$
$\emptyset\in\emptyset$
$\emptyset=\{\emptyset\}$
$\{\;\}=\emptyset$
$\emptyset\in\{\emptyset\}$

Вправа$\PageIndex{11}\label{ex:setintro-11}$

Визначте, які з наведених нижче тверджень є істинними, а які - помилковими.

$2\in(2,7)$
$\sqrt{2}\in(1,3)$
$\big(\sqrt{5}\,\big)^2\in\mathbb{Q}$
$-5\in\mathbb{N}$

Вправа$\PageIndex{12}\label{ex:setintro-12}$

Наведіть приклади наборів$A$,$B$ причому$C$ такі, що:

$A\in B$і$B\in C$, і$A \notin C$
$A\in B$і$B\in C$, і$A\in C$

Вправа$\PageIndex{13}\label{ex:setintro-13}$

Визначте, чи правильні чи синтаксично наведені нижче твердження. Для тих, хто синтаксично коректний, визначте їх значення істинності; для тих, які синтаксично невірні, запропонуйте способи їх виправлення.

$(3,7\,]=3<x\leq7$.
$\{x\in\mathbb{R}\mid x^2<0\} \equiv \emptyset$.

Вправа$\PageIndex{14}\label{ex:setintro-14}$

$\frac{7}{4}\in[2,\sqrt{7})$.
Не існує$x$ таких, що$x\in\mathbb{R}^+$ і$\mathbb{R}^-$.
Якщо$(0,\infty)$,$x$ то позитивний.