5.4: Додавання та віднімання раціональних виразів

Last updated
Save as PDF

Page ID: 59576

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Дріб - це пропорція. Дріб повідомляє кількість частин з цілого.

$\dfrac{a}{b} \dfrac{\textcolor{blue}{\longleftarrow \text{The part is the numerator.}}}{\textcolor{blue}{\longleftarrow \text{The whole is the denominator.}}}$

Наприклад, коробка для яєць, зображена нижче, містить$10$ яйце. Частина яєць коричнева ($7$яєць), а решта білі ($3$яєчні). Фракція$\dfrac{a}{b}$ швидко повідомляє частку яєць, які коричневі або білі. Пропорції також можуть бути вказані у вигляді десяткової або відсоткової величини.

$clipboard_e3c5408e1d01cd0704f558548ac275e13.png$

Пропорція коричневих яєць:$\dfrac{7}{10} = 7 ÷ 10 = 0.7 = 70 \%$

Пропорція білих яєць:$\dfrac{3}{10} = 3 ÷ 10 = 0.3 = 30 \%$

Пропорція коричневих і білих яєць описує всі яйцеклітини. Інтуїтивно ми знаємо, що ця пропорція є$100 \%$. Математика повинна відповідати нашій інтуїції, тому давайте досліджуємо.

$\begin{array} &70 \% + 30 \% &= 100 \% \\ \dfrac{7}{10} + \dfrac{3}{10} &= \dfrac{10}{10} \end{array}$

Наше дослідження змушує нас зробити висновок, що ми додаємо чисельники, але не знаменники.

Додавання або віднімання дробів (знаменник однаковий)

Додайте або відніміть чисельники.
Тримайте однаковий знаменник.
Зменшіть при необхідності.

\[\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a+b}{c}\]

Те, що працює для дійсних чисел, також працює для алгебраїчних величин. Алгебра дотримується тих же правил, що є відмінним якорем, з якого можна виконувати власні алгебраїчні дослідження.

Приклад Template:index

Додати$\dfrac{2x}{x+3} + \dfrac{x}{x+3}$

Рішення

Знаменники збігаються. Додайте два чисельника, але збережіть знаменник.

$\dfrac{2x}{x+3} + \dfrac{x}{x+3} = \dfrac{2x+x}{x+3} = \dfrac{3x}{x+3}$

Оскільки результат не може бути додатково спрощений, відповідь$\dfrac{3x}{x+3}$

Приклад Template:index

Віднімати$\dfrac{y^2+2y+8}{y^2−2y−15} − \dfrac{y^2+2}{y^2−2y−15}$

Рішення

Знаменники однакові. Відніміть чисельники. Пам'ятайте, що кожен чисельник - це величина.

$\begin{array} &\dfrac{y^2+2y+8}{y^2−2y−15} − \dfrac{y^2+2}{y^2−2y−15} &= \dfrac{y^2+2y+8−(y^2+2)}{y^2−2y−15} &\text{Numerator: subtract the quantity \((y^2 + 2)$.}\\ & =\ dfrac {y^2+2y+8−y^2−2} {y^2−2y−15} &\ text {Кожен член кількості віднімається.}\\ & =\ dfrac {2y+6} {y^2−2y−15} &\ text {Віднімання завершено.} \\ & =\ dfrac {2 (y+3)} {(y−5) (y+3)} &\ text {Факторний чисельник і знаменник. Скасувати.}\\ &=\ dfrac {2} {y−5} &\ text {Відповідь найбільш спрощена.} \ end {масив}\)

Додавання і віднімання з різними знаменниками

Для того щоб скласти раціональні числа або раціональні вирази, нам потрібно знайти спільний знаменник. Створюйте спільні знаменники, використовуючи еквівалентні дроби. Тобто,$\dfrac{a \cdot \textcolor{red}{d}}{b \cdot \textcolor{red}{d}} = \dfrac{ad}{bd}$. Потім скористайтеся процесом додавання дробів із загальними знаменниками.

Приклад Template:index

Додати$\dfrac{7}{75a^2b} + \dfrac{13}{180ab}$

Рішення

Щоб знайти найменш спільний знаменник, ми граємо в гру «у кого більше?» для кожного знаменника. Розбийте знаменники на прості множники. Уявіть, що кожен знаменник - це набір карт, а кожна карта - коефіцієнт знаменника. Оскільки у нас є два знаменника, у нас є два гравці, які гратимуть у гру, «у кого більше?». Який гравець має більшу частину фактора «виграє», і вони поміщають ці карти у виграшну купу. Готові грати?

Гравець #$1$:$75a^2 \longrightarrow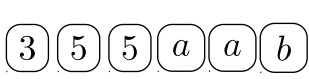$ $clipboard_e82900e65b6134c70d503b2fed4be7096.png$

Гравець #$2$:$180ab \longrightarrow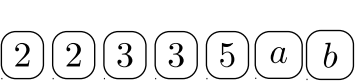$ $clipboard_ec69093ffe99e21d390dcc4c691e250bf.png$

У кого більше?	Гравець #$1$	Гравець #$2$	Виграшна купа
$2$'и		$\checkmark$	$2 \cdot 2$
$3$'и		$\checkmark$	$3 \cdot 3$
$5$'и	$\checkmark$		$5 \cdot 5$
$a$'и	$\checkmark$		$a \cdot a$
$b$'и	КРАВАТКА	КРАВАТКА	$b$

Виграшна купа$= 2^2 \cdot 3^2 \cdot 5^2 \cdot a^2 \cdot b$

Найменш спільний знаменник$= 900a^2b$

Використовуйте найменш спільний знаменник для створення спільного знаменника. Визначте, які фактори відсутні в кожному знаменнику. Помножте відсутні коефіцієнти на знаменник, а також на чисельник. Потім додаємо.

$\dfrac{7}{75a^2b} + \dfrac{13}{180ab} = \dfrac{7 \textcolor{red}{\cdot 12}}{75a^2b \textcolor{red}{\cdot 12}} + \dfrac{13 \textcolor{red}{\cdot 5a}}{180ab \textcolor{red}{\cdot 5a}} = \dfrac{84}{900a^2b} + \dfrac{65a}{900a^2b} = \dfrac{84+65a}{900a^2b} $.

Відповідь така:$\dfrac{84+65a}{900a^2b}$

Приклад Template:index

Додати$\dfrac{2y+1}{(4y+1)^2(y+6)} + \dfrac{5}{(4y+1)(y+6)}$

Рішення

У грі «у кого більше?» величини$(4y + 1)$ і$(y + 6)$ виступають як одиничні числа.

Гравець #$1$:$(4y + 1)^2 (y + 6) \longrightarrow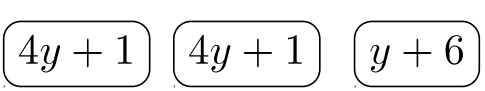$ $clipboard_ee200f708cfb0a13a36f0a1987aee86af.png$

Гравець #$2$:$(4y + 1)(y + 6) \longrightarrow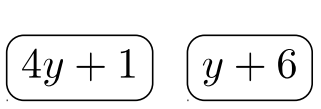$ $clipboard_e96fc9cb8c18dcb8c3ca506179e29e468.png$

Виграшна купа$(4y + 1)^2 (y + 6)$ = = Найменш спільний знаменник

$\begin{array} &\dfrac{2y+1}{(4y+1)^2(y+6)} + \dfrac{5}{(4y+1)(y+6)} &= \dfrac{2y+1}{(4y+1)^2(y+6)} + \dfrac{5 \textcolor{red}{\cdot (4y+1)}}{(4y+1)(y+6) \textcolor{red}{\cdot (4y+1)}} \\ &= \dfrac{2y+1+(20y+5)}{(4y+1)^2(y+6)} &\text{Simplify the numerator, but leave the denominator in factored form.} \\ &= \dfrac{22y+6}{(4y+1)^2(y+6)} &\text{The numerator is simplified. This is the answer!} \end{array}$

Порада: чисельник може бути врахований за допомогою GCF$= 2$:$22y + 6 = 2(11y + 3)$. Однак така факторизація не призводить до скасування. Тому віддається перевагу заявленому чисельнику.

Приклад Template:index

Віднімати$\dfrac{u^2+2u}{u^2+3u−10} − \dfrac{2u}{3u−6}$

Рішення

Щоб порівняти коефіцієнти кожного знаменника, нам потрібно коефіцієнт.

$ \begin{array} &&\dfrac{u^2+2u}{u^2+3u−10} − \dfrac{2u}{3u−6} = \dfrac{u^2+2u}{(u+5)(u−2)} − \dfrac{2u}{3(u−2)} &\text{The denominators are factored.} \end{array}$

Грайте в гру «у кого більше?» знайти найменш спільний знаменник. Величини виступають як одиничні числа.

Гравець #$1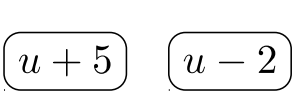$: $clipboard_e5b29d8142e8dc9709ca5f8f83c112282.png$

Гравець #$2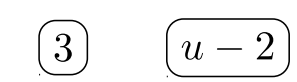$: $clipboard_e9db21ccf70da655263da0e7093153b56.png$

Виграшна купа$= 3(u + 5)(u − 2) =$ Найменш спільний знаменник

$\begin{array} &\dfrac{u^2+2u}{(u+5)(u−2)} − \dfrac{2u}{3(u−2)} &= \dfrac{\textcolor{red}{3}(u^2+2u)}{\textcolor{red}{3}(u+5)(u−2)} − \dfrac{2u \textcolor{red}{(u+5)}}{3(u−2) \textcolor{red}{(u+5)}} &\text{Determine the missing factors & multiply.} \\ &= \dfrac{3u^2+6u}{3(u+5)(u−2)} − \dfrac{2u^2+10u}{3(u+5)(u−2)} &\text{Simplify numerators.} \\ &= \dfrac{3u^2+6u−(2u^2+10u)}{3(u+5)(u−2)} &\text{Numerator: subtract the quantity.} \\ &= \dfrac{3u^2+6u−2u^2−10u}{3(u+5)(u−2)} &\text{Subtract each term of the quantity.} \\ &= \dfrac{u^2−4u}{3(u+5)(u−2)} &\text{The numerator is simplified. This is the answer!} \end{array}$

Порада: чисельник може бути врахований за допомогою GCF$= u$:$u^2 − 4u = u(u − 4)$. Однак така факторизація не призводить до скасування. Тому віддається перевагу заявленому чисельнику.

Приклад Template:index

Віднімати$\dfrac{3c}{49−c^2} − \dfrac{1}{c^2−7c}$

Рішення

Щоб порівняти коефіцієнти кожного знаменника, нам потрібно коефіцієнт.

$\begin{array} &&\dfrac{3c}{(7−c)(7+c)} − \dfrac{1}{c(c−7)} &\text{The denominators are factored.} \end{array}$

Грайте в гру «у кого більше?» знайти найменш спільний знаменник. Величини виступають як одиничні числа.

Гравець #$1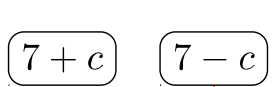$: $clipboard_e536c760e466e1d3499db5678220afecb.png$

Гравець #$2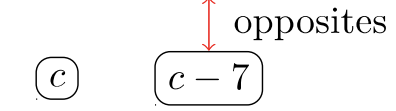$: $clipboard_e078fec96a07e13d83128820663fd76ea.png$

Примітка:$7 − c$ і$c − 7$ є протилежностями. Оскільки вони протилежні, одна величина може бути «схожа» на іншу.

$7 − c = −(c − 7)$

Далі відскакують негатив до чисельника. Вуаля! Ось як ми робимо найменш спільний знаменник.

Виграшна купа$= c(c + 7)(c − 7) =$ Найменш спільний знаменник

$\begin{array} &\dfrac{3c}{(7−c)(7+c)} − \dfrac{1}{c(c−7)} &= \dfrac{3c}{\textcolor{red}{−}(c−7)(7+c)} −\dfrac{1}{c(c−7)} &\text{Replace \(7 − c$с$−(c − 7)$.} \\ & =\ dfrac {\ textcolor {червоний} {−} 3c} {(c−7) (7+c)}} −\ dfrac {1} {c (c−7)} &\ текст {Оскільки$\dfrac{a}{−b} = \dfrac{-a}{b}$, покладіть мінус зверху.}\\ & =\ dfrac {−3c\ cdot\ textcolor {червоний} {c}} {textcolor {червоний} {c} (c−7) (c+7)} −\ dfrac {1\ textcolor {червоний} {\ cdot (c+7)}} {c (c−7)\ textcolor {червоний} {(c+7)}} &\ text {Побудувати РК-дисплей. Примітка:$7 + c = c + 7$.}\\ & =\ dfrac {−3c^2− (c+7)} {c (c−7) (c+7)} &\ text {Чисельник: відніміть кількість.}\\ &=\ dfrac {−3c^2−c−7} {c (c−7) (c+7) (c+7)} &\ text {Чисельник спрощено.}\ &=\ dfrac {− 3c^2+c+7} {c (c−7) (c+7)} &\ текст {Фактор поза$−1$.} \ end {масив}\)

Будь-який з останніх двох рядків може бути вашою остаточною відповіддю. Якому ви віддаєте перевагу? Це ваш вибір!

Примітка

Спростивши чисельник, зробіть паузу і запитайте себе: «Що ще можна зробити, щоб спростити?» Якщо чисельник є факторним, перевірте, чи однакові коефіцієнти, що й у знаменнику. Якщо так, скасуйте загальні фактори. Тримайте знаменник фактором, щоб нагадати собі (і своєму читачеві), які фактори не скасовують.

Спробуйте! (Вправи)

Для #1 -20 додайте або відніміть раціональні вирази, як зазначено.

$\dfrac{5x}{3y^2} + \dfrac{x}{3y^2}$
$\dfrac{14a}{5b} − \dfrac{4a}{5b}$
$\dfrac{4r}{9qp} + \dfrac{1}{3q^2p}$
$\dfrac{1−n}{6n} + \dfrac{2n+1}{3n}$
$\dfrac{n+2}{12m^3} − \dfrac{2}{3m^3n}$
$\dfrac{t+6}{t+5} + \dfrac{t+4}{t+5}$
$\dfrac{6c+1}{(5c+2)^3} − \dfrac{c−1}{(5c+2)^3}$
$\dfrac{2}{x−3} + \dfrac{3}{10}$
$\dfrac{4}{y+2} + \dfrac{2}{3y+6}$
$\dfrac{3}{x+3} − \dfrac{3}{x−3}$
$\dfrac{h−2}{(h+1)^2} + \dfrac{2}{3h+3}$
$\dfrac{5}{y−1} − \dfrac{3}{y^2−1}$
$\dfrac{−2}{a^2−5a+6} + \dfrac{2}{a−3}$
$\dfrac{4}{d−3} − \dfrac{5d−12}{d^2−6d+9}$
$\dfrac{5}{v^2−5v} − \dfrac{v}{5v−25}$
$\dfrac{1−n}{n^2−4} − \dfrac{n−2}{n^2−2n−8}$
$3 + \dfrac{x}{ x+2}$
$\dfrac{3p−1}{p^2+5p+6} + \dfrac{2p−3}{p^2+3p+2}$
$\dfrac{3}{q+3} + \dfrac{2q}{q^2+8q+15}$
$\dfrac{w+2}{4w+16} − \dfrac{2}{w^2+4w}$

Для #21 -30 відбуваються протилежні величини. Додайте або відніміть раціональні вирази, як зазначено.

$\dfrac{3}{8} + \dfrac{5}{−8}$
$\dfrac{y^2}{y−5} + \dfrac{4y+5}{5−y}$
$\dfrac{6}{w−2} + \dfrac{w+3}{2−w}$
$\dfrac{2a−7}{5a−8} + \dfrac{6+10a}{8−5a}$
$\dfrac{u^2−2}{2u^2−u−3} + \dfrac{u−2}{3−2u}$
$\dfrac{b−23}{b^2−b −20} − \dfrac{2}{5−b}$
$\dfrac{t+1}{t−1} − \dfrac{3t^2−1}{1−t^2}$
$\dfrac{2}{6−3x} + \dfrac{x}{x^2−4}$
$\dfrac{5r}{1−2r} − \dfrac{2r}{2r+1} + \dfrac{3}{4r^2−1}$
$\dfrac{2y}{y^2−9} − 1 + \dfrac{4}{3−y}$

У кого більше?	Гравець #\(1\)	Гравець #\(2\)	Виграшна купа
\(2\)'и		\(\checkmark\)	\(2 \cdot 2\)
\(3\)'и		\(\checkmark\)	\(3 \cdot 3\)
\(5\)'и	\(\checkmark\)		\(5 \cdot 5\)
\(a\)'и	\(\checkmark\)		\(a \cdot a\)
\(b\)'и	КРАВАТКА	КРАВАТКА	\(b\)