2.3: Огляд факторингу
- Page ID
- 59476
Факторинг є необхідним навиком, щоб мати в пречислення і всі математичні класи поза пречислення. Факторинг - це інструмент для спрощення виразів і полегшення розрахунків. Це допомагає нам визначити коріння поліномів, роблячи швидку роботу графіків без необхідності комп'ютерів або графічних калькуляторів. Таким же чином арифметичні правила інформують алгебраїчні властивості, проста факторизація дійсних чисел інформує поліноми факторизації. Наступні дійсні числа були враховані у добуток простих чисел:
\(\begin{array} &36 &= 2 \cdot 2 \cdot 3 \cdot 3 \\ 40 &= 2 \cdot 2 \cdot 2 \cdot 5 \\ 45 &= 3 \cdot 3 \cdot 5 \\ 455 &= 5 \cdot 7 \cdot 13 \end{array}\)
Поліноміальна факторизація моделює одне і те ж поняття: розбивають многочлен вниз на добуток його простих многочленів.
У цьому розділі будуть описані наступні методики факторингу:
- Найбільший загальний фактор (GCF)
- Триміальна факторизація:\(x^2 − bx + c\)
- Триноміальна факторизація:\(ax^2 − bx + c\) де\(a \neq 1\).
- Різниця квадратів
- Ідеальні квадратні триноми
- Різниця кубів
- Сума кубів
Найбільший загальний фактор (GCF)
Подумайте про факторинг GCF як про зворотний (або скасування) розподільної властивості.
\(\xrightarrow{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\text{multiply}} \\ a(b+c+d + ...) = a(b) + a(c) + a(d)+ ... \\ \xleftarrow[\text{factor}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;]{\text{}} \)
Щоб знайти GCF, перерахуйте фактори кожного терміну. Визначте загальні фактори. Потім коефіцієнт за допомогою методу GCF, як показано на прикладі нижче.
Фактор триноміалу\(16x^5 + 8x^3 − 4x^2\).
Рішення
Розбийте кожен з\(3\) термінів триноміалу на його фактори наступним чином:
\(\begin{array} &16x^5 &= \textcolor{red}{2} \cdot \textcolor{blue}{2} \cdot 2 \cdot 2 \cdot \textcolor{green}{x} \cdot \textcolor{pink}{x} \cdot x \cdot x \cdot x \\ 8x^3 &= \textcolor{red}{2} \cdot \textcolor{blue}{2} \cdot 2 \cdot \textcolor{green}{x} \cdot \textcolor{pink}{x} \cdot x \\ 4x^2 &= \textcolor{red}{2} \cdot \textcolor{blue}{2} \cdot \textcolor{green}{x} \cdot \textcolor{pink}{x} \end{array}\)
\(2 \cdot 2 \cdot x \cdot x = \textcolor{red}{4x^2 = \text{GCF}}\)
Наступний крок: зарахуйте GCF з кожного з умов.
Усередині дужок збережіть розміщення трьох термінів та операції додавання та віднімання:
\(\textcolor{red}{\text{GCF}}(\textcolor{green}{\text{Term 1}} + \textcolor{green}{\text{Term 2}} - \textcolor{green}{\text{Term 3}} )\).
Відповідь Факторна форма многочлена є\(4x^2(4x^3 + 2x -1)\)
Примітка: Ви можете перевірити свою відповідь за допомогою властивості distributive. Цей крок є необов'язковим, але, помноживши факторну форму, ви засвоїте поняття, що продукт є оригінальним поліном.

Порада: Факторизація GCF завжди є першою технікою, яку слід шукати в будь-якому поліномі. Іноді многочлен вимагатиме декількох різних методів факторингу, щоб повністю зарахувати многочлен.
Тримінал факторизації x 2+ bx+c
Якщо провідний коефіцієнт триноміала\(2^{\text{nd}}\) ступеня дорівнює\(1\), ми можемо перерахувати триноміал у добуток двох біноміалів:\((x + m)(x + n)\). Дві умови на\(m\) і\(n\) повинні дотримуватися:
\(\left. \begin{array}{ll} mn = c\\ m + n =b \end{array} \right\} \text{Factoring Technique} \Longrightarrow x^2 + bx + c = (x + m)(x + n) \)
Фактор триноміалу\(x^2 −x − 12\).
Рішення
Подумайте про пару цілих чисел,\(m\) і\(n\), такі, що дві умови тримають:
\(\left. \begin{array}{ll} mn = -12\\ m + n = -1 \end{array} \right\}\)
Можливі значення\(m\), (n\):
| Продукт є\(−12\) | Успіх, якщо сума є\(−1\), |
| \((−1)(12) = −12 \\ (1)(−12) = −12\) | \( \left.\begin{array}{ll} \textcolor{red}{\times}\;\; − 1+ 12 = −11\\ \textcolor{red}{\times} \;\;12 + (−1) = 11 \end{array} \right\} \text{opposites} \) |
| \((−2)(6) = −12 \\ (2)(−6) = −12\) | \( \left.\begin{array}{ll} \textcolor{red}{\times} \;\;− 2+ 6 = 4\\ \textcolor{red}{\times} \;\;2 + (−6) = −4 \end{array} \right\} \text{opposites} \) |
| \((−3)(4) = −12 \\ (3)(−4) = −12\) | \( \left.\begin{array}{ll} \textcolor{red}{\times} \;\;−3 + 4 = 1\\ \textcolor{green}{\checkmark} \;\;3 + (−4) = −1 \end{array} \right\} \text{opposites} \) |
Відповідь Факторна форма\(x^2 − x − 12\) є\((x + 3)(x − 4)\).
Примітка: Ви можете перевірити свою відповідь за допомогою методу FOIL. Цей крок є необов'язковим, але, помноживши факторну форму, ви засвоїте поняття, що продукт є оригінальним поліном.
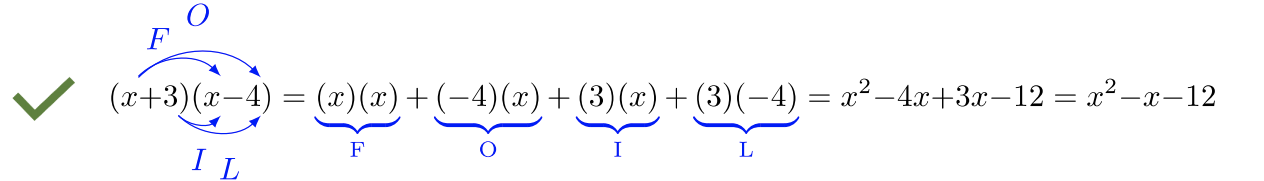
Деякі многочлени є простими, що означає, що многочлен не може бути врахований. Якщо кожен можливий метод факторингу зазнає невдачі, поліном є простим поліномом.
Тримінал факторизації Макс 2 + x x x x, де a ≠ 1
Якщо провідний коефіцієнт триноміала\(2^{\text{nd}}\) ступеня не є\(1\), для множника множника буде потрібно більше проб і помилок. Мета, як і у випадку\(a=1\), полягає у створенні двох біноміалів, які при множенні на метод FOIL виробляють заданий многочлен. Однак\(a\) значення −value додасть більше спроб випробувань. Не забувайте, що деякі поліноми є простими і не можуть бути враховані. Наведені нижче кроки орієнтують ваш підхід до факторингу.
Крок 1: Чи є GCF в триноміалі? Фактор загальне значення, якщо ви знайдете його.
Крок 2: Перерахуйте пари факторів\(a\) і пари факторів\(c\).
Крок 3: Побудувати біноми. Заповніть\(4\) поля відповідним чином.

Крок 4: F O IL: O uter = великий смайлик-особа. Внутрішній = маленька смайлик-особа. Помножте, щоб знайти Зовнішній і Внутрішній F O IL. Знайдіть вдалу комбінацію таку, що Outer + Внутрішня\(= bx =\) цільова сума.

Крок 5: Тримайте\(a\) -фактори фіксованими, але подумайте про зворотні\(c\) -фактори, якщо випробування не вдається виробити\(bx\).
Крок 6: Якщо всі комбінації факторів не дають Цільової суми\(bx\), триноміал є простим.
Фактор\(2x^2 + 3x + 1\)
Рішення
Перший термін триноміалу - це\(2x^2\). Так як\(a \neq 1\), давайте пройдемося по кожному кроку:
Крок 1: GCF\(= 1\), тому немає загальних факторів.
Крок 2: Перерахуйте пари факторів\(a\) і з\(c\):
| \(a = 2\) | \(c = 1\) |
| \(\textcolor{red}{2 \cdot 1}\) | \(\textcolor{blue}{1 \cdot 1}\) |
Крок 3:\((\textcolor{red}{2}x + \textcolor{blue}{1})(\textcolor{red}{1}x + \textcolor{blue}{1}) \)
Крок 4: Давайте перевіримо Зовнішній і Внутрішній, щоб переконатися, що їх сума є\(bx = 3x\).

\(\text{Outer } + \text{ Inner } = 2x + x = 3x\)
Успіху! Ми знайшли правильну факторизацію!
Відповідь: Факторна форма тріумфу\(2x^2 + 3x + 1 = (2x+1)(x+1)\)
Фактор\(6t^2 − 28t + 16\)
Рішення
Крок 1: GCF\(=2\). Фактор з загального фактора:\(2(3t^2 − 14t + 8)\)
Крок 2: Перерахуйте пари факторів\(a\) і з\(c\):
Зверніть увагу, що цільова сума є негативною.
\(bx = −14t\)
Однак\(c\) є позитивним. Ці\(c\) -фактори повинні бути негативними (див. Таблицю нижче)
| \(a=3\) | \(c=8\) |
| \(\textcolor{red}{3 \cdot 1}\) | \(\textcolor{blue}{-8 \cdot -1}\) |
| \(\textcolor{blue}{-4 \cdot -2}\) |
Крок 3: Помістіть\(a\) -фактори, а потім виберіть пару\(c\) -факторів. Оскільки цільова сума є\(−14t\), більш імовірно, що менші числа будуть успішними.
Пробна версія 1:\(2(\textcolor{red}{3}t − \textcolor{blue}{4})(\textcolor{red}{1}t − \textcolor{blue}{2})\)
Крок 4: Давайте перевіримо Зовнішній і Внутрішній.
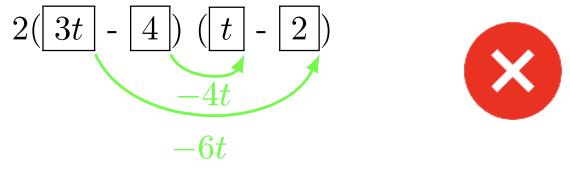
Пробний процес 1 не вдається. \(−4t − 6t \neq −14t\)
Пробна версія 2:\(2(\textcolor{red}{3}t − \textcolor{blue}{2})(\textcolor{red}{1}t − \textcolor{blue}{4})\)
Крок 5: Давайте перевіримо Зовнішній і Внутрішній

Проба 2 - це успіх! \(−12t − 2t = −14t\)
Відповідь\(6t^2 − 28t + 16 = 2(3t-2)(t-4)\). Тримінал повністю врахований.
Різниця квадратів
Нижче наведено три приклади, які демонструють візерунок після використання методу FOIL.
| Помножте біноміали | Фольга метод | Спрощений результат | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| \((x + 3)(x − 3)\) | \(=\) | \(x^2 + \underbrace{−3x + 3x}_{\text{O + I cancels}} −3 \cdot 3\) | \(=\) | \(x^2 − 9\) | ||||||
| \((y-10)(y+10)\) | \(=\) | \(y^2 + \underbrace{+10y - 10y}_{\text{O + I cancels}} −10 \cdot 10\) | \(=\) | \(y^2 - 100\) | ||||||
| \((n^2 + 4)(n^2 − 4)\) | \(=\) | \(n^4 + \underbrace{-4n^2 + 4n^2}_{\text{O + I cancels}} −4 \cdot 4\) | \(=\) | \(n^4-16\) | ||||||
Два бічлена множаться. Один - сполучений інший. Тобто в одному біном\(x\) і\(a\) додаються, а в іншому\(x\) і\(a\) віднімаються. Зверніть увагу, що зовнішні і внутрішні терміни завжди скасовують один одного за цим шаблоном.
Спеціальний продукт = Різниця квадратів:\((A+B)(A-B) = A^2 - B^2\)
Факторинг - це зворотне множення. Для того, щоб фактор, ми повинні розквадратувати ідеальні квадрати, створивши продукт:
\(\xrightarrow{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\text{multiply}} \\ (x+a)(x-a) = \underbrace{x^2-a^2}_{\text{difference of squares}} \\ \xleftarrow[\text{factor}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;]{\text{}} \)
Фактор:\(n^2 − 64\)
Рішення
Обидва терміни є ідеальними квадратами. Ми будемо використовувати формулу Спеціальний продукт у зворотному напрямку:\(A^2 − B^2 = (A + B)(A − B)\). Для того, щоб фактор, нам потрібен unsquare кожного члена!

Ось,\(A=n\) і\(B=8\). Формула керує нашим факторингом:
\(\begin{array} &&(A+B)(A-B) \\ &(n+8)(n-8) \end{array}\)
Відповідь\(n^2 − 64 = (n+8)(n-8)\)
Фактор повністю. \(4x^2y − 81x\)
Рішення
При факторингу перше, на що слід звернути увагу, це найбільший загальний фактор (GCF). Обидва члени многочлена поділяють множник\(y\). Після факторингу GCF ми враховуємо дужки як різницю квадратів.
\(4x^2y - 81y\)
GCF\(= y\) Фактор з GCF
\(=y(4x^2-81)\)
Різниця квадратів\(A=2x\) і\(B=9\)
\(=y(2x+9)(2x-9)\)
Слово «різниця» перекладається як «віднімання». Різниця квадратів вимагає віднімання між двома квадратними термінами:\(A^2 − B^2\). Крім загальних факторів, сума квадратів не\(A^2 + B^2\) є факторною.
Фактор\(n^2 + 25\).
Рішення
Хоча обидва терміни є ідеальними квадратами, це не різниця квадратів. Операція між квадратами не є відніманням. GCF\(=1\). Оскільки ми не можемо виділити загальний фактор, ми робимо висновок, що\(n^2 + 25\) це простий многочлен.
Ідеальні квадратні триноми
Інша закономірність з'являється, коли множаться два однакових бічлена. Нижче наведено три приклади, які демонструють візерунок після використання методу FOIL.
| Помножте біноміали | Фольга метод | Спрощений результат | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| \((t + 5)(t + 5)\) | \(=\) | \(t^2 + \underbrace{−5t + 5t}_{\text{O + I} = 2(5t)} + 5^2\) | \(=\) | \(t^2 + 10t + 25\) | ||||||
| \((2y − 9)(2y − 9)\) | \(=\) | \((2y)^2 - \underbrace{18y - 18y}_{\text{O + I} =2(2y)(−10)} + 9^2\) | \(=\) | \(4y^2 − 36y + 81\) | ||||||
| \((pq + 7)(pq + 7)\) | \(=\) | \((pq)^2 + \underbrace{7pq + 7pq}_{\text{O + I} =2(7pq)} + 7^2\) | \(=\) | \(p^2q^2 + 14pq + 49\) | ||||||
Спеціальний продукт = Ідеальний квадратний Trinomial
\( \begin{array} &&(A + B)^2 = (A + B)(A + B) = A^2 + 2AB + B^2 \\ &(A − B)^2 = (A − B)(A − B) = A^2 − 2AB + B^2 \end{array} \)
Факторинг - це зворотне множення. Для того, щоб фактор, визначити неквадрат першого і останнього члена. Тобто знайти\(A\) і\(B\), потім слідувати формулам вище.
Фактор\(25n^2 − 90n + 81\)
Рішення
Тримінал має GCF\(= 1\). Однак перший і останній члени - ідеальні квадрати, а многочлен - тріноміал. Давайте подивимося, чи нам дали ідеальний квадратний триноміал.
- Зіставте формулу з заданим триноміалом.
- Визначте значення\(A\) і\(B\).
- Перевірте, що\(2AB\) також збігається.
- Символ мінус є основною підказкою, яка говорить нам, яку спеціальну формулу продукту ми будемо використовувати.
- \(A^2 − 2AB + B^2 = (A − B)^2\)
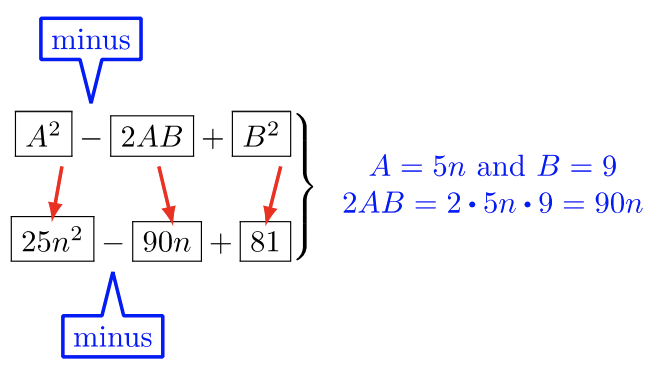
Обов'язково переконайтеся, що\(2AB\) також відповідає даному середньому терміну. У\(2.3.8\) прикладі нам дали Perfect Square Trinomial, тому що\(2AB\) збігалися з середнім терміном,\(90n\). Тому ми можемо зарахувати цей триноміал за допомогою формули факторингу Perfect Square Trinomials.
Відповідь:\(25n^2 − 90n + 81 = (5n-9)^2\)
Увага: Якщо многочлен не може бути врахований одним методом факторингу, це не обов'язково означає, що многочлен є простим. Не здавайся! Вичерпніть всі можливі методи факторингу, перш ніж зробити висновок, що поліном є простим.
Фактор\(9y^2 + 15y + 4\)
Рішення
GCF\(=1\). Однак перший і останній члени - ідеальні квадрати, а многочлен - тріноміал. Давайте подивимося, чи нам дали ідеальний квадратний триноміал.

Зіставивши терміни, визначаємо\(A = 3y\) і\(B = 2\). Однак\(2AB = 12y\) не відповідає заданому середньостроковому терміну\(15y\). Триноміал не є ідеальним квадратним триноміалом.
Однак триноміал не є простим. Це може бути враховано за допомогою методу trial-and-error.
Крок 1: GCF\(=1\). Загального фактора немає.
Крок 2: Перерахуйте пари факторів\(a\) і з\(c\): (див. діаграму нижче).
| \(a=9\) | \(c=4\) |
| \(\textcolor{red}{9 \cdot 1}\) | \(\textcolor{blue}{4 \cdot 1}\) |
| \(\textcolor{red}{3 \cdot 3}\) | \(\textcolor{blue}{2 \cdot 2}\) |
\(bx = 15y = \text{ Target Sum}\)
Крок 3: Помістіть a-фактори, а потім виберіть пару\(c\) -факторів. Ми вже знаємо, що\((3y + 2)(3y + 2)\) не працює. Спробуємо:\((3y + 4)(3y + 1)\)
Крок 4: Давайте перевіримо Зовнішній і Внутрішній
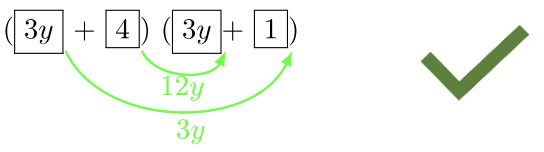
Цей судовий процес має успіх! \(12y + 3y = 15y\)
Інші випробування, які зазнають невдачі:
| \((3y + 2)(3y + 2)\) | \(6y + 6y= 12y\) | \(\neq 15y\) |
| \((9y + 4)(y + 1)\) | \(4y + 9y = 13y\) | \(\neq 15y\) |
| \((9y + 1)(y + 4)\) | \(y+36y=37y\) | \(\neq 15y\) |
Відповідь\(9y^2 + 15y + 4 = (3y+4)(3y+1)\).
Факторна сума кубів та різниця кубів
Для того, щоб визначити правильну стратегію факторингу, непогано запам'ятати хоча б перші п'ять кубів. Формули, наведені нижче, направляють наш факторинг.
\(\begin{array} &&1^3 = 1 \\ &2^3 = 8 \\ &3^3 = 27 \\&4^3 = 84 \\&5^3 = 125 \end{array}\)
Факторинг сум і відмінностей кубів
\(\begin{array} &&A^3 + B^3 = (A + B)(A^2 − AB + B^2 ) \\ &A^3 − B^3 = (A − B)(A^2 + AB + B^2 ) \end{array}\)
Фактор\(27 − 8m^3\)
Рішення
Біноміал - це різниця кубиків.
Використовуйте формулу з\(A = 3\) і\(B = 2m\).

\(27 − 8m^3 = (3 − 2m)(9 + 6m + 4m^2)\)
Спробуйте! (Вправи)
Фактор #1 -3 наступний за допомогою факторизації GCF:
- \(12u − 6u^2\)
- \(10x^3y + 15xy^2\)
- \(12z^3 − 9z^2 − 3z\)
Фактор #4 -6 використовуючи трійну факторизацію:
- \(t^2 + 2t - 15\)
- \(h^2 − 12h + 20\)
- \(r^2 + 14r + 24\)
Фактор #7 -12, що використовує як GCF, так і тріноміальну факторизацію:
- \(3b^2 + 12b + 9\)
- \(4q^2 − 4q − 80\)
- \(x^3 − 11x^2 + 10x\)
- \(2a^2b + 24ab − 56b\)
- \(7x^4 + 49x^3 + 70x^2\)
- \(3n^2m − 12mn − 63m\)
Фактор #13 -18 з використанням триноміальної факторизації, де провідний коефіцієнт\(\neq 1\).
- \(2d^2 − 9d − 18\)
- \(3h^2 − 29h + 18\)
- \(7t^2 + 17t − 12\)
- \(4y^2 − 3y − 7\)
- \(10n^2 − 11n − 8\)
- \(8x^2 + 6x − 9\)
Фактор #19 -24 з використанням різниці квадратів факторизації:
- \(r^2 − 100\)
- \(81 − h^2\)
- \(4t^2 − 1\)
- \(25 − n^4\)
- \(v^4 − 36\)
- \(16p^2 − 25q^2\)
Фактор #25 -27 використовуючи формулу суми кубів:
- \(c^3 + 125\)
- \(27 + 64n^3\)
- \(1 + a^6\)
Фактор #28 -30 з використанням різниці кубів формули:
- \(q^3 − 8\)
- \(125d^3 − 27\)
- \(64u^3 − v^3\)
Фактор #31 -36 за допомогою будь-якого відповідного методу. Фактор повністю.
- \(30m^2 − 5m − 5\)
- \(2c^2 − 8\)
- \(h^4 − 81\)
- \(6p^3q + 6q\)
- \(15k^3 − 2k^2 − k\)
- \(a^2b^2 − a^2\)
- Що таке простий многочлен? Наведіть\(3\) приклади простих триноміалів.
- Наведіть приклад суми квадратів. Чи є це факторним? Поясніть.
- Число\(64\) є одночасно ідеальним квадратом і кубом. Які ще числа є і квадратом, і кубом? Як ви думаєте, їх всього кілька або нескінченно багато?
