Skip to main content
LibreTexts - Ukrayinska

5.3: Десяткові операції (частина 1)

  1. Last updated
  2. Save as PDF
  • Page ID
    57915

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Цілі навчання
    • Додавання та віднімання десяткових знаків
    • Множення десяткових знаків
    • Ділимо десяткові
    • Використовуйте десяткові знаки в грошових додатках
    будьте готові!

    Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.

    1. Спростити\(\dfrac{70}{100}\). Якщо ви пропустили цю проблему, перегляньте приклад 4.3.1.
    2. Помножити\(\dfrac{3}{10} \cdot \dfrac{9}{10}\). Якщо ви пропустили цю проблему, перегляньте приклад 4.3.7.
    3. Ділимо −36 ÷ (−9). Якщо ви пропустили цю проблему, перегляньте приклад 3.7.3.

    Додавання та віднімання десяткових знаків

    Давайте ще раз подивимося на порядок обіду з початку Десяткових знаків, цього разу помітивши, як цифри були складені разом.

    \[\begin{split} & $3.45 \quad Sandwich \\ & $1.25 \quad Water \\ + & $0.33 \quad Tax \\ \hline & $5.03 \quad Total \end{split}\]

    Всі три предмети (сендвіч, вода, податок) були оцінені в доларах і центах, тому ми вишикували долари під доларами, а центи під центами, а десяткові крапки вишикувалися між ними. Тоді ми просто додали кожен стовпець, як якщо б ми додавали цілі числа. Вибудовуючи десяткові числа таким чином, ми можемо додати або відняти відповідні значення місця так само, як ми робили з цілими числами.

    ЯК: ДОДАВАННЯ АБО ВІДНІМАННЯ ДЕСЯТКОВИХ ЗНАКІВ

    Крок 1. Запишіть цифри вертикально, щоб десяткові крапки вибудовувалися.

    Крок 2. Використовуйте нулі в якості власників місця, якщо потрібно.

    Крок 3. Додайте або відніміть числа так, ніби вони були цілими числами. Потім помістіть десяткову кому у відповіді під десятковими крапками в заданих числах.

    Приклад\(\PageIndex{1}\):

    Додайте: 3,7+12,4.

    Рішення

    Запишіть цифри вертикально, щоб десяткові крапки вибудовувалися. $\ begin {спліт} 3. &7\\ + 12. &4\\\ hline\ кінець {спліт} $$
    Місцеві утримувачі не потрібні, оскільки обидва числа мають однакову кількість десяткових знаків.  
    Складіть числа так, ніби вони цілі числа. Потім помістіть десяткову кому у відповіді під десятковими крапками в заданих числах. $$\ begin {спліт}\ стекер {1} {3}. &7\\ + 12. &4\\\ лінія 16. &1\ кінець {спліт} $$
    Вправа\(\PageIndex{1}\):

    Додайте: 5,7 + 11,9.

    Відповідь

    \(17.6\)

    Вправа\(\PageIndex{2}\):

    Додайте: 18.32 + 14.79.

    Відповідь

    \(13.11\)

    Приклад\(\PageIndex{2}\):

    Додайте: 23,5 + 41,38.

    Рішення

    Запишіть цифри вертикально, щоб десяткові крапки вибудовувалися. $\ begin {спліт} 23. &5\\ + 41. &38\\\ hline\ кінець {спліт} $$
    Помістіть 0 як місце власника після 5 в 23.5, так що обидва числа мають два знака після коми. $\ begin {спліт} 23. &5\ колір тексту {червоний} {0}\\ + 41. &38\\\ hline\ кінець {спліт} $$
    Складіть числа так, ніби вони цілі числа. Потім помістіть десяткову кому у відповіді під десятковими крапками в заданих числах. $\ begin {спліт} 23. &50\\ + 41. &38\\\ лінія 64. &88\ кінець {спліт} $$
    Вправа\(\PageIndex{3}\):

    Додайте: 4,8 + 11,69.

    Відповідь

    \(16.49\)

    Вправа\(\PageIndex{4}\):

    Додайте: 5.123 + 18.47.

    Відповідь

    \(23.593\)

    Скільки змін ви б отримали, якби передали касиру рахунок у 20 доларів за покупку в 14.65 доларів? Ми покажемо кроки для обчислення цього в наступному прикладі.

    Приклад\(\PageIndex{3}\):

    Відніміть: 20 − 14,65.

    Рішення

    Запишіть цифри вертикально, щоб десяткові крапки вибудовувалися. Пам'ятайте, що 20 - це ціле число, тому розмістіть десяткову крапку після 0. $\ begin {спліт} 20. &\\ - 14. &65\\\ hline\ кінець {спліт} $$
    Помістіть два нулі після десяткової крапки в 20, як місця, щоб обидва числа мали два знака після коми.

    \[\begin{split} 20.& \textcolor{red}{00} \\ - 14.&65 \\ \hline \end{split}\]
    Відніміть числа так, ніби вони цілі числа. Потім помістіть десяткову кому у відповіді під десятковими крапками в заданих числах. $$\ begin {спліт}\ стекер {1} {\ cancel {2}}\ стекер {\ stackerl {9} {\ cancel {10}}} {\ cancel {0}} &. \ стекер {\ стекерл {9} {\ скасувати {10}}} {\ скасувати {0}}\ стекерл {\ stackerl {9} {\ скасувати {10}}} {\ cancel {0}}\ - 1\;\; 4\;\; &\; 6\;\; 6\;\; 5\\ hline 5\;\;\;\;\; 3;\; 5\ кінець {спліт} $$
    Вправа\(\PageIndex{5}\):

    Відніміть: 10 − 9,58.

    Відповідь

    \(0.42\)

    Вправа\(\PageIndex{6}\):

    Відніміть: 50 − 37,42.

    Відповідь

    \(12.58\)

    Приклад\(\PageIndex{4}\):

    Відніміть: 2,51 − 7,4.

    Рішення

    Якщо відняти 7.4 з 2.51, відповідь буде негативною, починаючи з 7.4 > 2.51. Щоб легко відняти, ми можемо відняти 2,51 з 7.4. Потім помістимо негативний знак в результат.

    Запишіть цифри вертикально, щоб десяткові крапки вибудовувалися. $\ begin {спліт} 7. &4\\ - 2. &51\\\ hline\ кінець {спліт} $$
    Поставте нуль після 4 в 7.4 як тримач місця, так що обидва числа мають два знака після коми. $\ begin {спліт} 7. &4\ колір тексту {червоний} {0}\\ - 2. &51\\\ hline\ кінець {спліт} $$
    Відніміть і помістіть десяткове число у відповіді. $\ begin {спліт} 7. &40\\ - 2. &51\\\ лінія 4. &89\ кінець {спліт} $$
    Пам'ятайте, що ми дійсно віднімаємо 2,51 − 7.4, тому відповідь негативна. 2.51 − 7.4 = − 4.89
    Вправа\(\PageIndex{7}\):

    Відніміть: 4,77 − 6,3.

    Відповідь

    \(-1.53\)

    Вправа\(\PageIndex{8}\):

    Відніміть: 8,12 − 11,7.

    Відповідь

    \(-3.58\)

    Множення десяткових знаків

    Множення десяткових знаків дуже схоже на множення цілих чисел - ми просто повинні визначити, де розмістити десяткову крапку. Процедура множення десяткових знаків матиме сенс, якщо ми спочатку розглянемо множення дробів.

    Ви пам'ятаєте, як множити дроби? Щоб помножити дроби, ви множите чисельники, а потім множите знаменники. Отже, давайте подивимося, що ми отримаємо як добуток десяткових знаків, перетворюючи їх у дроби в першу чергу. Ми зробимо два приклади пліч-о-пліч у таблиці 5.22. Шукайте викрійку.

    Таблиця\(\PageIndex{1}\)
    A Б
      (0.3) (0.7) (0.2) (0.46)
    Перетворити на дробові дроби. $$\ ліворуч (\ dfrac {3} {10}\ праворуч)\ ліворуч (\ dfrac {7} {10}\ праворуч) $$ $$\ ліворуч (\ dfrac {2} {10}\ праворуч)\ ліворуч (\ dfrac {46} {100}\ праворуч) $$
    Помножити. $$\ фрак {21} {100} $$ $$\ фрак {92} {100} $$
    Перетворити назад до десяткових знаків 0,21 0.092

    Є візерунок, який ми можемо використовувати. У A ми помножили два числа, кожне з яких має один десятковий знак, а добуток мав два знака після коми. У B ми помножили число з одним десятковим знаком на число з двома знаками після коми, а твір мав три знака після коми.

    Скільки знаків після коми ви очікуєте для добутку (0,01) (0,004)? Якщо ви сказали «п'ять», ви розпізнали закономірність. Коли ми множимо два числа з десятковими знаками, ми підраховуємо всі десяткові розряди у факторах - у цьому випадку два плюс три - щоб отримати кількість десяткових знаків у продукті - у цьому випадку п'ять.

    Верхній рядок говорить 0,01 раз 0,004 дорівнює 0,00004. Нижче 0.01 він говорить 2 місця. Нижче 0.004 він говорить про 3 місця. Нижче 0.00004, він говорить про 5 місць. У нижньому рядку сказано, що 1 більше 100 разів 4 понад 1000 дорівнює 4 понад 100 000.

    Як тільки ми знаємо, як визначити кількість цифр після десяткової крапки, ми можемо помножити десяткові числа, не перетворюючи їх у дроби спочатку. Число десяткових знаків у добутку - це сума кількості десяткових знаків у множниках.

    Правила множення позитивних і негативних чисел стосуються і десяткових знаків теж, звичайно.

    Визначення: Множення двох чисел

    При множенні двох чисел

    • якщо їх ознаки однакові, продукт позитивний.
    • якщо їх ознаки різні, продукт негативний.

    Коли ви множите знакові десяткові числа, спочатку визначте знак добутку, а потім помножте так, ніби числа обидва позитивні. Нарешті, напишіть виріб відповідним знаком.

    ЯК: МНОЖИТИ ДЕСЯТКОВІ ЧИСЛА

    Крок 1. Визначте ознаку вироби.

    Крок 2. Напишіть цифри у вертикальному форматі, вибудовуючи цифри праворуч.

    Крок 3. Помножте числа так, ніби вони цілі числа, тимчасово ігноруючи десяткові крапки.

    Крок 4. Розставте десяткову крапку. Число десяткових знаків у добутку - це сума кількості десяткових знаків у множниках. Якщо потрібно, використовуйте нулі як заповнювачі.

    Крок 5. Напишіть виріб відповідним знаком.

    Приклад\(\PageIndex{5}\):

    Множимо: (3,9) (4,075).

    Рішення

    Визначте ознаку вироби. Прикмети ті ж. Продукт буде позитивним.
    Напишіть цифри у вертикальному форматі, вибудовуючи цифри праворуч. $\ begin {спліт} 4.07&5\\\ раз 3. &9\\\ hline\ кінець {спліт} $$
    Помножте числа так, ніби вони цілі числа, тимчасово ігноруючи десяткові крапки. $\ begin {спліт} 4.07&5\\\ раз 3. &9\\\ hline 3667&5\\ 12225&\;\\\ hline 15892&5\ кінець {спліт} $$
    Розставте десяткову крапку. Додайте кількість десяткових знаків у множниках (1 + 3). Поставте десяткову крапку на 4 розряди праворуч. $\ begin {спліт} 4.07&5\ quad\ textcolor {синій} {3\; місця}\\\ раз 3. &9\ квадратний\ колір тексту {синій} {1\; місце}\\ hline 3667&5\\ 12225&\;\\ hline 15892&5\ quad\ textcolor {синій} {4\; місця}\ кінець {спліт} $$
    Продукт позитивний. (3,9) (4.075) = 15,8925
    Вправа\(\PageIndex{9}\):

    Множення: 4,5 (6,177).

    Відповідь

    \(27.4815\)

    Вправа\(\PageIndex{10}\):

    Множення: 10,79 (8,12).

    Відповідь

    \(87.6148\)

    Приклад\(\PageIndex{6}\):

    Помножте: (−8,2) (5.19).

    Рішення

    Прикмети бувають різні. Продукт буде негативним.
    Пишіть у вертикальному форматі, вишикуючи цифри праворуч. $\ begin {спліт} 5. &19\\\ раз 8. &2\\\ hline\ кінець {спліт} $$
    Помножити. $\ begin {спліт} 5. &19\\\ раз 8. &2\\\ hline 10&38\\ 415&2\;\\\ hline 425&58\ кінець {спліт} $$
    $\ begin {спліт} 5. &19\\\ раз 8. &2\\\ hline 10&38\\ 415&2\;\\\ hline 42.5&58\ кінець {спліт} $$
    Продукт негативний. (−8.2) (5.19) = −42,558
    Вправа\(\PageIndex{11}\):

    Помножте: (4,63) (−2,9).

    Відповідь

    \(-13.427\)

    Вправа\(\PageIndex{12}\):

    Помножте: (−7,78) (4,9).

    Відповідь

    \(-38.122\)

    У наступному прикладі нам потрібно буде додати кілька заповнювачів нулів, щоб правильно розмістити десяткову крапку.

    Приклад\(\PageIndex{7}\):

    Множимо: (0,03) (0,045).

    Рішення

    Продукт позитивний. (0.03) (0.045)
    Пишіть у вертикальному форматі, вишикуючи цифри праворуч. $\ почати {спліт} 0.04&5\\\ раз 0,0&3\\ hline\ кінець {спліт} $$
    Помножити. $\ почати {спліт} 0.04&5\\\ раз 0,0&3\\\ hline 13&5\ кінець {спліт} $$

    Додайте нулі в міру необхідності, щоб отримати 5 місць.
    Продукт позитивний. (0.03) (0.045) = 0,00135
    Вправа\(\PageIndex{13}\):

    Множимо: (0,04) (0,087).

    Відповідь

    \(0.00348\)

    Вправа\(\PageIndex{14}\):

    Множимо: (0.09) (0.067).

    Відповідь

    \(0.00603\)

    Помножте на сили 10

    У багатьох галузях, особливо в науках, прийнято множити десяткові числа на ступені 10. Давайте подивимося, що станеться, коли ми помножимо 1,9436 на деякі сили 10.

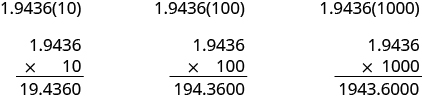
    Верхній ряд говорить 1,9436 раз 10, потім 1,9436 раз 100, потім 1,9436 раз 1000. Нижче кожного знаходиться вертикальна задача множення. Вони показують, що 1,9436 разів 10 є 19,4360, 1,9436 разів 100 - 194,3600, а 1,9436 разів 1000 - 1943,6000.

    Подивіться на результати без кінцевих нулів. Ви помічаєте закономірність?

    \[\begin{split} 1.9436(10) & = 19.436 \\ 1.9436(100) & = 194.36 \\ 1.9436(1000) & = 1943.6 \end{split}\]

    Кількість знаків, на які перемістилася десяткова крапка, збігається з кількістю нулів у степені десяти. У таблиці 5.26 підсумовуються результати.

    Таблиця\(\PageIndex{2}\)
    Помножити на Кількість нулів Кількість знаків після коми
    10 1 1 місце праворуч
    100 2 2 місця праворуч
    1 000 3 3 місця праворуч
    10 000 4 4 місця праворуч

    Ми можемо використовувати цей шаблон як ярлик для множення на повноваження десять замість множення за допомогою вертикального формату. Ми можемо порахувати нулі в ступені 10, а потім перемістити десяткову крапку, що ж з місць вправо. Так, наприклад, щоб помножити 45,86 на 100, перемістіть десяткову крапку на 2 розряди вправо.

    45.86 разів 100 показано рівним 4586. Існує стрілка з десяткового переходу на 2 місця від після 5 до після 6.

    Іноді, коли нам потрібно перемістити десяткову крапку, не вистачає десяткових знаків. У цьому випадку ми використовуємо нулі як заповнювачі. Наприклад, помножимо 2,4 на 100. Нам потрібно перемістити десяткову крапку на 2 розряди вправо. Оскільки праворуч від десяткової крапки є лише одна цифра, ми повинні записати 0 на сотих місцях.

    У 2,4 рази 100 показано рівним 240. Існує стрілка з десяткової коми переходить через 2 місця після 2 до після 0.

    ЯК: ПОМНОЖИТИ ДЕСЯТКОВУ КОМУ НА СТУПІНЬ 10

    Крок 1. Перемістіть десяткову крапку вправо на ту ж кількість знаків, що і кількість нулів в ступені 10.

    Крок 2. Запишіть нулі в кінці числа як заповнювачі, якщо потрібно.

    Приклад\(\PageIndex{8}\):

    Помножте 5,63 на множники (a) 10 (b) 100 (c) 1000.

    Рішення

    Дивлячись на кількість нулів, кратних десяти, ми бачимо кількість знаків, які нам потрібно перемістити десяткове вправо.

    (а) 5.63 (10)

    Існує 1 нуль в 10, тому перемістіть десяткову крапку на 1 місце вправо.
      56.3

    (б) 5.63 (100)

    Є 2 нулі в 100, тому перемістіть десяткову крапку на 2 розряди вправо.
      563

    (с) 5.63 (1000)

    Є 3 нулі в 1000, тому перемістіть десяткову крапку на 3 розряди вправо.
    В кінці потрібно додати нуль. 5 630
    Вправа\(\PageIndex{15}\):

    Помножте 2,58 на множники (a) 10 (b) 100 (c) 1000.

    Відповідь на

    \(25.8\)

    Відповідь б

    \(258\)

    Відповідь c

    \(2,580\)

    Вправа\(\PageIndex{16}\):

    Помножте 14,2 на множники (a) 10 (b) 100 (c) 1000.

    Відповідь на

    \(142\)

    Відповідь б

    \(1,420\)

    Відповідь c

    \(14,200\)

    Дописувачі та атрибуція