1.S: Цілі цифри (резюме)

Last updated
Save as PDF

Page ID: 57740

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Ключові умови

координувати	Число в парі з точкою на числовій лінії.
підрахунок чисел	Підрахувальні числа - це цифри 1, 2, 3,...
різниця	Результат віднімання двох і більше чисел.
дивідендів	Число, яке ділиться при діленні двох чисел.
дільник	Число, що ділить дивіденд при діленні двох чисел.
номер рядка	Для візуалізації чисел використовується числовий рядок. Числа на числовому рядку стають більшими, оскільки вони йдуть зліва направо, і менше, коли вони йдуть справа наліво.
походження	Точка з позначкою 0 на числовому рядку.
місце вартість система	Наша система числення називається системою значень місця, тому що значення цифри залежить від її положення, або місця, в числі.
продукт	Результат множення двох і більше чисел.
частка	Результат ділення двох чисел.
округлення	Процес наближення числа.
сума	Результат додавання двох і більше чисел.
цілих чисел	Цілими числами є числа 0, 1, 2, 3,...

Ключові концепції

1.1 - Вступ до цілих чисел

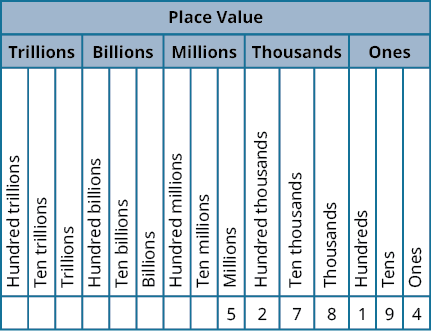
$Діаграма під назвою «Place Value» з п'ятнадцятьма стовпцями та 4 рядками, зі стовпцями, розбитими на п'ять груп по три. Рядок заголовка показує трильйони, мільярди, мільйони, тисячі та одиниці. Наступний ряд має значення «Сто трильйонів», «Десять трильйонів», «трильйони», «сто мільярдів», «десять мільярдів», «сто мільйонів», «десять мільйонів», «мільйони», «сто тисяч», «десять тисяч», «сотні», «десятки» та «одиниці». Перші 8 значень у наступному рядку є порожніми. Починаючи з дев'ятого стовпця, значеннями є «5», «2», «7», «8», «1», «9» та «4».$

Назвіть ціле число прописом.
1. Починаючи з цифри зліва, назвіть число в кожному періоді, а потім - назва періоду. Не включайте назву періоду для них.
2. Використовуйте коми в числі, щоб відокремити періоди.
Використовуйте значення місця, щоб записати ціле число.
1. Визначте слова, які вказують на періоди. (Пам'ятайте, що ті період ніколи не названий.)
2. Намалюйте три заготовки, щоб вказати кількість місць, необхідних в кожному періоді.
3. Назвіть номер у кожному періоді та розмістіть цифри у правильній позиції значення місця.
Округляйте ціле число до певного значення місця.
1. Знайдіть задане значення місця. Всі цифри зліва від цього місця не змінюються.
2. Підкресліть цифру праворуч від заданого значення місця.
3. Визначте, чи ця цифра більше або дорівнює 5. Якщо так — додайте 1 до цифри у вказаному значенні місця. Якщо ні — не змінюйте цифру в заданому місці значення.
4. Замініть всі цифри праворуч від заданого значення місця нулями.

1.2 - Додати цілі числа

• Додавання позначення: Щоб описати додавання, ми можемо використовувати символи та слова.

Операція	Позначення	Вираз	Читати як	Результат
Додавання	+	3 + 4	три плюс чотири	сума 3 і 4

Ідентифікаційна властивість додавання: Сума будь-якого числа a та 0 - це число. $$\ begin {спліт} a + 0 &= a\\ 0 + a &= a\ кінець {спліт} $$
Комутативна властивість додавання: Зміна порядку доповнень a та b не змінює їх суму. $а+ б = б + а\ ldotp$$
Додайте цілі числа.

Запишіть числа так, щоб кожне місце значення вибудовувалося вертикально.
Додайте цифри в кожному місці значення. Працюйте справа наліво, починаючи з тих місць. Якщо сума у значенні місця більше 9, перенесіть на наступне місце значення.
Продовжуйте додавати значення кожного місця справа наліво, додаючи кожне значення місця та переносячи, якщо потрібно.

1.3 - Відніміть цілі числа

Операція	Позначення	Вираз	Читати як	Результат
Віднімання	-	7 - 3	вісім мінус три	різниця 7 і 3

Відніміть цілі числа.

Запишіть числа так, щоб кожне місце значення вибудовувалося вертикально.
Відніміть цифри в кожному місці значення. Працюйте справа наліво, починаючи з тих місць. Якщо цифра зверху менше, ніж цифра нижче, запозичуйте в міру необхідності.
Продовжуйте віднімати кожне значення місця справа наліво, запозичуючи при необхідності.
Перевірте шляхом додавання.

1.4 - Множення цілих чисел

Операція	Позначення	Вираз	Читати як	Результат
множення	×	3 × 8	три рази вісім	продукт 3 і 8
	•	3 • 8
	()	3 (8)

Властивість множення нуля: добуток будь-якого числа і 0 дорівнює 0. $$\ почати {спліт} a\ cdot 0 &= 0\\ 0\ cdot a &= 0\ кінець {спліт} $$
Властивість ідентичності множення: добуток будь-якого числа і 1 - це число. $$\ begin {спліт} 1\ cdot a &= a\ a\ cdot 1 &= a\ кінець {спліт} $$
Комутативна властивість множення: Зміна порядку факторів не змінює їх добутку. $а\ точка б = б\ точка а\ ldotp$$
Помножте два цілих числа, щоб знайти твір.

Запишіть числа так, щоб кожне місце значення вибудовувалося вертикально.
Помножте цифри в кожному місці значення.
Працюйте справа наліво, починаючи з тих, що розміщуються в нижньому номері.
Помножте нижнє число на цифру одиниць у верхньому числі, потім на цифру десятків і так далі.
Якщо товар в місці значення більше 9, перенесіть на наступне місце значення.
Напишіть часткові вироби, вибудовуючи цифри в значення місця з цифрами вище. Повторіть для десятків місце в нижньому числі, сотні місце і так далі.
Вставте нуль як заповнювач з кожним додатковим частковим твором.
Додайте часткові продукти.

1.5 - Розділіть цілі числа

Операція	Позначення	Вираз	Читати як	Результат
Відділ	÷	12 ÷ 4	Дванадцять розділених на чотири	частка 12 і 4
	$\dfrac{a}{b}$	$\dfrac{12}{4}$
	$b \overline{) a}$	$4 \overline{\smash{)}12}$
	а/б	12/4

Властивості поділу одного:
- Будь-яке число (крім 0), розділене саме по собі, дорівнює одиниці. $а\ дів а = 1$$
- Будь-яке число, розділене на одиницю, є однаковим числом. $$а\ дів 1 = а$$
Властивості поділу нуля:
- Нуль ділиться на будь-яке число 0. $$0\ div a = 0 $$
- Ділення числа на нуль не визначено. $$a\ div 0 = невизначено$$
Розділіть цілі числа.

Ділимо першу цифру дивіденду на дільник. Якщо дільник більше першої цифри дивіденда, розділіть перші дві цифри дивіденду на дільник і так далі.
Напишіть коефіцієнт вище дивідендів.
Помножте частку на дільник і запишіть добуток під дивідендом.
Відніміть цей продукт із дивідендів.
Збиваємо наступну цифру дивідендів.
Повторюйте з кроку 1, поки не буде більше цифр у дивіденді, щоб збити.
Перевірте, множивши частку на дільник.