Skip to main content
LibreTexts - Ukrayinska

3.2: Явні граничні умови

  1. Last updated
  2. Save as PDF
  • Page ID
    61102

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Для задач, що цікавлять тут, ми розглянемо лише лінійні крайові умови, які виражають лінійне співвідношення між функцією та її частинними похідними, наприклад,\[u(x,y=0) + x \frac{\partial u}{\partial x}(x,y=0)=0. \nonumber \] як і раніше максимальний порядок похідної в граничній умові на порядок нижче порядку PDE. Для диференціального рівняння другого порядку ми маємо три можливі типи граничних умов.

    Крайова умова Діріхле

    Коли ми вказуємо значення\(u\) на межі, ми говоримо про граничні умови Діріхле. Прикладом для вібруючої струни з її кінцями, в\(x=0\) і\(x=L\), закріпленими буде

    \[u(0,t) = u(L,t) = 0. \nonumber \]

    Граничні умови фон Неймана

    У багатовимірних задачах похідна функції w.r.t. до кожної зі змінних утворює векторне поле (тобто функцію, яка приймає векторне значення в кожній точці простору), зазвичай називається градієнтом. Для трьох змінних це набуває вигляду\[\mbox{grad} \space f(x,y,z) = {\nabla} f(x,y,z) = \left (\frac{\partial f}{\partial x}(x,y,z),\frac{\partial f}{\partial y}(x,y,z),\frac{\partial f}{\partial z}(x,y,z)\right ). \nonumber \]

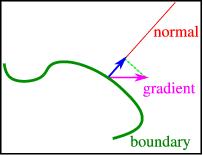
    vonNeuman.png

    Рисунок\(\PageIndex{1}\): Ескіз нормальних похідних, що використовуються в граничних умовах фон Неймана.

    Зазвичай ми не можемо вказати градієнт на кордоні, оскільки це занадто обмежує, щоб дозволити рішення. Ми можемо — а у фізичних задачах часто потрібно — вказати компонент нормаль до межі, див.\(\PageIndex{1}\) Рис. Коли ця нормальна похідна вказана, ми говоримо про граничні умови фон Неймана.

    У разі ізольованого (нескінченно тонкого) стрижня довжини\(a\), ми не можемо мати тепловий потік за кінцями, щоб градієнт температури повинен зникнути (тепло може протікати тільки там, де існує різниця температур). Це призводить до БК

    \[\frac{\partial u}{\partial x}(0,t) = \frac{\partial u}{\partial x}(a,t) = 0. \nonumber \]

    Змішані (Робіна) граничні умови

    Звичайно, ми можемо змішати граничні умови Діріхле та фон Неймана. Для прикладу тонкого стрижня, наведеного вище, ми могли б зажадати

    \[u(0,t) + \frac{\partial u}{\partial x}(0,t) = u(a,t) + \frac{\partial u}{\partial x}(a,t) = 0. \nonumber \]