3.3.1: Приклади

Last updated
Save as PDF

Page ID: 61754

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Приклад 3.3.1.1: Рівняння Белтрамі

\ begin {екнаррей}
\ мітка {belt1}\ тег {3.3.1.1}
WU_X-BV_X-CV_Y&=&0\
\ мітка {belt2}\ тег {3.3.1.2}
WU_Y+AV_X+BV_Y&=&0,
\ end {eqnarray}

де$W,\ a,\ b,\ c$ задані функції в залежності від$(x,y)$,$W\not=0$ і матриця

$
\ ліворуч (\ begin {масив} {cc}
a&b\
b&c
\ end {масив}\ праворуч)
\]

є позитивним певним.

Система Бельтрамі є узагальненням рівнянь Коші-Рімана. Функція$f(z)=u(x,y)+iv(x,y)$, де$z=x+iy$, називається квазівідповідним відображенням, див. Наприклад [9], Глава 12, для застосування до рівнянь з частинними похідними.

Набір

$
A^1=\ лівий (\ begin {масив} {cc}
W&-b\\
0&a
\ end {масив}\ праворуч),\\
A^2=\ left (\ begin {масив} {cc}
0&-c\\
w&b
\ end {масив}\ праворуч).
\]

Тоді систему (\ ref {belt1}), (\ ref {belt2}) можна записати як

$
A^1\ left (\ begin {масив} {c}
u_x\ v_x
\ кінець {масив}\ праворуч) +
A^2\ ліворуч (\ begin {масив} {c}
u_y
\ end {масив}\ право) =\ left (\ begin {масив} {c} 0\ end {масив}\ праворуч).
\]

Таким чином,

\ begin {екнаррай*}
C (x, y,\ зета) =\ ліворуч |\ почати {масив} {cc}
W\ zeta_1&-b\ zeta_1-c\ zeta_2\\
W\ zeta_2&a\ zeta_1+b\ zeta_2
\ кінець {масив}\ право|
= W (a\ zeta_1^2+2b zeta_1\ zeta_2+c\ zeta_2^2),
\ end {екнаррай*}

який відрізняється від нуля, якщо$\zeta\not=0$ за вищевказаними припущеннями. Таким чином, система Бельтрамі є еліптичною.

Приклад 3.3.1.2: Рівняння Максвелла

Рівняння Максвелла в ізотропному випадку

\ begin {eqnarray}
\ мітка {max1}\ тег {3.3.1.3}
c\\ текст {rot} _x\ H &=&\ лямбда E+\ epsilon e_t\
\ мітка {max2}\ тег {3.3.1.4}
c\ text {rot} _x\ E&=&-\ mu H_t,
\ end {eqnarray}

де

$E=(e_1,e_2,e_3)^T$напруженість електричного поля$e_i=e_i(x,t)$,$x=(x_1,x_2,x_3)$,
$H=(h_1,h_2,h_3)^T$напруженість магнітного поля$h_i=h_i(x,t)$,
$c$швидкість світла,
$\lambda$питома провідність,
$\epsilon$постійна діелектричність,
$\mu$магнітна проникність.

Ось$c,\ \lambda,\ \epsilon$ і$\mu$ позитивні константи.

Набір$p_0=\chi_t,\ p_i=\chi_{x_i}$$i=1,\ldots 3$, то характерне диференціальне рівняння

$
\ ліворуч |\ почати {масив} {cccccc}
\ епсилон p_0/c&0&0&0&p_3&-p_2\\
0&\ епсилон
p_0/c&0&-p_3&0&0&0&0&0&епсилон p_0/c&-2&-p_1&0\\
0&0&0 p_3&p_2&\ му р_0/с&0&0\\
p_3&0&-p_1&0&\ му p_0/c&0\\
-p_2&p_1&0&0&\ му p_0/c
\ кінець {масив}\ право|= 0.
\]

Наступні маніпуляції спрощують це рівняння:

Перші три стовпці множимо на$\mu p_0/c$,
помножте 5-й стовпець з$-p_3$ і 6-й стовпець з$p_2$ і додайте суму до 1-го стовпця,
помножте 4-й стовпець з$p_3$ і 6-й стовпець з$-p_1$ і додайте суму до 2-го стовпця,
помножте 4-й стовпець з$-p_2$ і 5-й стовпець з$p_1$ і додайте суму до 3-го стовпця,
розгорніть отриманий визначник щодо елементів 6-го, 5-го і 4-го ряду.

Отримуємо

$
\ ліворуч |\ почати {масив} {ccc}

q+p_1^2&p_1p_2&p_1p_3\\
p_1p_2&q+p_2^2&p_2p_3\\ p_1p_3&q+p_3^2
\ кінець {масив}\ право|=0,
\]

де

$
q: =\ frac {\ епсилон\ му} {c^2} p_0^2-g^2
\]

с$g^2:=p_1^2+p_2^2+p_3^2$. Оцінка вищевказаного рівняння призводить до$q^2(q+g^2)=0$, тобто,

$
\ chi_t^2\ ліворуч (\ frac {\ epsilon\ mu} {c^2}\ chi_t^2-|\ nabla_x\ chi|^2\ праворуч) =0.
\]

Відразу випливає, що рівняння Максвелла - це гіперболічна система, див. Вправу.
Існує два розв'язки цього характеристичного рівняння. Перші - це характерні поверхні$\mathcal{S}(t)$, визначені тим$\chi(x,t)=0$, які задовольняють$\chi_t=0$. Ці поверхні називаються стаціонарними хвилями. Другий тип характерних поверхонь визначається розчинами

$
\ frac {\ епсилон\ му} {c^2}\ chi_t^2=|\ nabla_x\ chi|^2.
\]

Функції,$\chi=f(n\cdot x-Vt)$ визначені, є розв'язками цього рівняння.
Ось$f(s)$ довільна функція з$f'(s)\not=0$,$n$ є одиничним вектором і$V=c/\sqrt{\epsilon\mu}$.
Пов'язані$\mathcal{S}(t)$ характерні поверхні визначаються

$
\ чі (х, т)\ екв f (n\ cdot Х-ВТ) =0,
\]

Тут ми припускаємо, що$0$ знаходиться в діапазоні$f:\ \mathbb{R}^1\mapsto\mathbb{R}^1$. Таким чином,$\mathcal{S}(t)$ визначається тим$n\cdot x-Vt=c$, де$c$ знаходиться фіксована константа. Звідси випливає, що площини$\mathcal{S}(t)$ з нормальною швидкістю$n$ рухаються$V$ у напрямку$n$, див. Малюнок 3.3.1.1.

$альт$

Малюнок 3.3.1.1:$d'(t)$ це швидкість плоских хвиль

$V$називається швидкістю плоскої хвилі$\mathcal{S}(t)$.

Зауваження. Згідно з попередніми обговореннями, особливості розв'язку рівнянь Максвелла розташовані максимум на характерних поверхнях.

Окремим випадком рівнянь Максвелла є телеграфні рівняння, які випливають з рівнянь Максвелла if$\text{\div}\ E=0$ і$\text{div}\ H=0$$ i. e.,$E$ і$H$ є полями, вільними від джерел. Насправді, достатньо припустити, що це припущення задовольняється$t_0$ лише у встановлений час, див. Вправу.

Так як

$
\ текст {rot} _x\\ текст {rot} _x\ A=\ mbox {град} _x\\ текст {div} _x\ A-\ трикутник_ха
\]

для кожного$C^2$ -векторного поля$A$ з рівнянь Максвелла випливає незв'язана система

\ begin {екнаррай*}\ трикутник_xe&= &\ frac {\ epsilon\ му} {c^2} E_ {tt} +\ frac {\ лямбда\ му} {c^2} E_t\
\ трикутник_xh&=&\ frac {\ epsilon\ mu} {c^2} H_ {tt} +\ frac {\ лямбда\ му} {c^2} h_t.
\ end {еканаррай*}

Приклад 3.3.1.3: Рівняння газодинаміки

Розглянемо наступні квазілінійні рівняння першого порядку.

$$
v_t+ (v\ cdot\ nabla_x)\ v+\ frac {1} {\ rho}\ nabla_x p =f\\\ mbox {(рівняння Ейлера)}.
\]

Ось

$v=(v_1,v_2,v_3)$вектор швидкості$v_i=v_i(x,t)$,$x=(x_1,x_2,x_3)$,
$p$тиск$p=(x,t)$,
$\rho$щільність$\rho=\rho(x,t)$,
$f=(f_1,f_2,f_3)$щільність зовнішньої сили$f_i=f_i(x,t)$,

$(v\cdot\nabla_x)v\equiv (v\cdot\nabla_x v_1,v\cdot\nabla_x v_2,v\cdot\nabla_x v_3))^T$.

Друге рівняння

$
\ rho_t+v\ cdot\ nabla_x\ rho+\ rho\\ text {div} _x\ v=0\\\ mbox {(збереження маси)}.
\]

Припустимо, що газ стисливий і що існує функція (рівняння стану)

$
р=р (\ рхо),
\]

де$p'(\rho)>0$ якщо$\rho>0$. Тоді вищевказана система з чотирьох рівнянь

\ begin {eqnarray}
\ мітка {лінійка}\ тег {3.3.1.5}
v_t+ (v\ cdot\ nabla) v+\ frac {1} {\ rho} p' (\ rho)\ nabla\ rho&=&f\\
\ етикетка {cont}\ тег {3.3.1.6}
\ rho_t+\ rho\ text {div}\ v+v\ dot\ nabla\ rho&=&0,
\ end {екнаррей}

де$\nabla\equiv\nabla_x$ і$\text{div}\equiv\text{div}_x$, тобто, ці оператори застосовуються лише до просторових змінних.

Характерне диференціальне рівняння тут
$$
\ left|\ begin {масив} {cccc}
\ frac {d\ chi} {dt} &0&\ frac {1} {\ rho} p'\ chi_ {x_1}\\
0&\ frac {d\ chi} {dt} &0&\ frac {1} {\ rho} p'\ chi_ {xi_ {xi_ {xi_ {x_ _2}\\
0&0&\ розриву {d\ chi} {dt} &\ розриву {1} {\ rho} p '\ chi_ {x_3}\\ rho
\ chi_ {x_1} &\ rho\ chi_ {x_2} &\ rho\ chi_ {x_3} &\ frac {d\ chi} {dt}
\ кінець {масив}\ right|= 0,
\]

де

$\ dfrac {д\ чі} {dt} :=\ chi_t+ (\ nabla_x\ chi)\ cdot v.\]

Оцінюючи детермінанту, отримаємо характеристичне диференціальне рівняння

\ begin {рівняння}
\ мітка {chargas}\ тег {3.3.1.7}
\ лівий (\ frac {d\ chi} {dt}\ праворуч) ^2\ ліворуч (\ frac {d\ chi} {dt}\ праворуч) ^2-p '(\ rho) |\ nabla_x\ chi|^2\ праворуч) =0.
\ end {рівняння}

Це рівняння має на увазі наслідки для швидкості характерних поверхонь, як показує наступний розгляд.

Розглянемо$\mathcal{S}(t)$ сімейство поверхонь в$\mathbb{R}^3$ визначається$\chi(x,t)=c$, де
$x\in\mathbb{R}^3 $ і$c$ є фіксованою константою. Як зазвичай, ми припускаємо, що$\nabla_x\chi\not=0$.
Одна з двох нормалей на$\mathcal{S}(t)$ точці поверхні$\mathcal{S}(t)$ задається, див. вправу,
\ begin {рівняння}
\ label {surfnormal}\ tag {3.3.1.8}
{\ bf n} =\ frac {\ nabla_x\ chi} {|\ nabla_x\ chi|}.
\ end {рівняння}
Нехай$Q_0\in\mathcal{S}(t_0)$ і нехай$Q_1\in\mathcal{S}(t_1)$ буде точкою на лінії$Q_0+s{\bf n}$, визначеної, де${\bf n}$ нормаль (\ ref {surfnormal}) на$\mathcal{S}(t_0)$ at$Q_0$ і$t_0<t_1$,$t_1-t_0$ мала, див. Рис. 3.3.1.2.

$альт$

3.3.1.2: Визначення швидкості поверхні

Визначення. Обмеження
$$
P=\ lim_ {t_1\ to t_0}\ frac {|Q_1-Q_0|} {t_1-t_0}
$$
називається швидкістю поверхні$\mathcal{S}(t)$.

Пропозиція 3.2. Швидкість поверхні$\mathcal{S}(t)$ дорівнює
\ begin {рівняння}
\ label {speedsurf}
P=-\ frac {\ chi_t} {|\ nabla_x\ chi|}.
\ end {рівняння}

Доказ. Доказ випливає з$\chi(Q_0,t_0)=0$ і$\chi(Q_0+d{\bf n},t_0+\triangle t)=0$, де$d=|Q_1-Q_0|$ і$\triangle t=t_1-t_0$.

$\Box$

Встановити$v_n:=v\cdot{\bf n}$, який є складовою вектора швидкості в напрямку${\bf n}$.
З ({\ ref {surfnormal}) отримуємо
$
v_n=\ frac {1} {|\ nabla_x\ chi|} v\ cdot\ nabla_x\ chi.
\]

Визначення. $V:=P-v_n$, Різниця швидкості поверхні і швидкості рідких частинок, називається відносною швидкістю.

$альт$

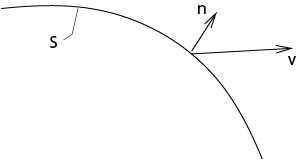
Малюнок 3.3.1.3: Визначення відносної швидкості

Використовуючи$P$ наведені вище формули для і$v_n$ слід
$
v=p-v_n=-\ frac {\ chi_t} {|\ nabla_x\ chi|} -\ frac {v\ cdot\ nabla_x\ chi} {|\ nabla_x\ chi|} дт}.
$$
Тоді з характеристичного рівняння (\ ref {chargas}), що
$$
V^2|\ nabla_x\ chi|^2\ left (V^2|\ nabla_x\ chi|^2-p '(\ rho) |\ nabla_x\ chi|^2\ праворуч) =0.
$$
Цікавим висновком є те, що існує дві відносні швидкості:$V=0$ або$V^2=p'(\rho)$.

Визначення. $\sqrt{p'(\rho)}$називається швидкістю звуку.