6: Стабільні та нестабільні многовиди рівноваг
- Page ID
- 61136
Для гіперболічних рівноваг автономних векторних полів лінеаризація фіксує локальну поведінку поблизу рівноваг для нелінійного векторного поля. Наведено результати, які обґрунтовують це твердження в контексті двовимірних автономних систем.
Розглянуто\(C^r\)\(r \ge 1\) двовимірне автономне векторне поле наступного вигляду:
\(\dot{x} = f(x,y)\),
\[\dot{y} = g(x, y), (x, y) \in \mathbb{R}^2. \label{6.1}\]
Нехай\(\phi_{t}(\cdot)\) позначають потік, що генерується (6.1). Припустимо,\((x_{0}, y_{0})\) це гіперболічна точка рівноваги цього векторного поля, тобто два власні значення якобійської матриці:
\(\begin{pmatrix} {\frac{\partial f}{\partial x}(x_{0},y_{0})}&{\frac{\partial f}{\partial y}(x_{0},y_{0})}\\ {\frac{\partial g}{\partial x}(x_{0},y_{0})}&{\frac{\partial g}{\partial y}(x_{0},y_{0})} \end{pmatrix}\)
- \((x_{0}, y_{0})\)є джерелом для лінеаризованого векторного поля,
- \((x_{0}, y_{0})\)є раковиною для лінеаризованого векторного поля,
- \((x_{0}, y_{0})\)є сідлом для лінеаризованого векторного поля.
Кожен випадок ми розглядаємо індивідуально.
- В даному випадку\((x_{0}, y_{0})\) є джерелом для (6.1). Точніше, існує сусідство U\((x_{0}, y_{0})\) такого, що для будь-якого\(p \in U\),\(\phi_{t}(p)\) залишає U у міру збільшення.
- В даному випадку\((x_{0}, y_{0})\) це раковина для (6.1). Точніше, існує сусідство S\((x_{0}, y_{0})\) такого, що для будь-якого\(p \in S\),\(\phi_{t}(p)\) наближається\((x_{0}, y_{0})\) з експоненціальною швидкістю, коли вона збільшується. В даному\((x_{0}, y_{0})\) випадку приклад притягує безліч і його басейн тяжіння наведено:
\(B \equiv \bigcup_{t \le 0} \phi_{t}(S).\)
- Для випадку гіперболічних сідлових точок структура сідлової точки все ще зберігається поблизу точки рівноваги для нелінійних систем. Ми зараз пояснимо, що саме це означає. Для того, щоб це зробити, нам потрібно буде більш уважно вивчити (6.1). Зокрема, нам потрібно буде перетворити (6.1) в систему координат, яка «локалізує» поведінку поблизу точки рівноваги і конкретно відображає структуру лінійної частини. Ми вже робили це кілька разів, вивчаючи поведінку поблизу конкретних рішень, тому не будемо повторювати ці деталі.
Трансформуючись локально поблизу\((x_{0}, y_{0})\) таким чином, ми можемо висловити (6.1) у наступному вигляді:
\[\begin{pmatrix} {\dot{\zeta}}\\ {\dot{\eta}} \end{pmatrix} = \begin{pmatrix} {-\alpha}&{0}\\ {0}&{\beta} \end{pmatrix} \begin{pmatrix} {\zeta}\\ {\eta} \end{pmatrix}+ \begin{pmatrix} {u(\zeta, \eta)}\\ {v(\zeta, \eta)} \end{pmatrix}, \alpha, \beta > 0, (\zeta, \eta) \in \mathbb{R}^2, \label{6.2}\]
де якобійський за походженням,
\[\begin{pmatrix} {-\alpha}&{0}\\ {0}&{\beta} \end{pmatrix}, \label{6.3}\]
відображає гіперболічний характер точки рівноваги. Лінеаризація (6.1) про походження дається:
\[\begin{pmatrix} {\dot{\zeta}}\\ {\dot{\eta}} \end{pmatrix} = \begin{pmatrix} {-\alpha}&{0}\\ {0}&{\beta} \end{pmatrix} \begin{pmatrix} {\zeta}\\ {\eta} \end{pmatrix}, \label{6.4}\]
Легко помітити для лінеаризованої системи, яка
\[E^s = {(\zeta, \eta)|\eta = 0}, \label{6.5}\]
є інваріантним стійким підпростором і
\[E^u = {(\zeta, \eta)|\zeta = 0}, \label{6.6}\]
є інваріантним нестабільним підпростором.
Викладено, як ця структура сідлової точки успадковується нелінійною системою шляхом постановки результатів стабільної та нестійкої теореми багатовидів гіперболічних рівноваг для двовимірних неавтономних векторних полів.
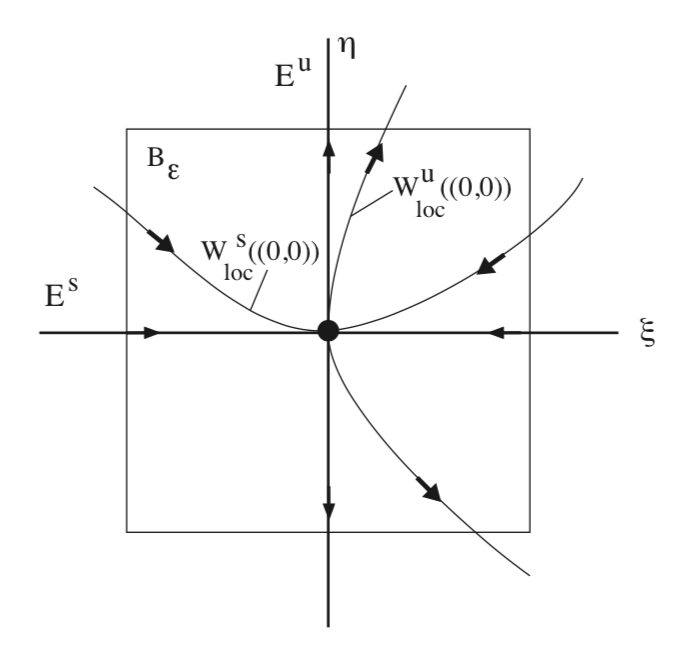
Спочатку розглянемо два інтервали осей координат, що містять початок, наступним чином:
\[I_{\zeta} \equiv {-\epsilon < \zeta < \epsilon}, \label{6.7}\]
і
\[I_{\eta} \equiv {-\epsilon < \eta < \epsilon}, \label{6.8}\]
для деяких дрібних\(\epsilon > 0\). Околиці походження будуються шляхом взяття декартового добутку цих двох інтервалів:
\[B_{\epsilon} \equiv \{(\zeta, \eta) \in \mathbb{R}^2|(\zeta, \eta) \in I_{\zeta} \times I_{\eta}\}, \label{6.9}\]
і це проілюстровано на рис.6.1. Теорема про стабільність та нестабільність багатовидів гіперболічних точок рівноваги автономних векторних полів говорить наступне.
Існує\(C^r\) крива, задана графіком функції\(\zeta\) змінних:
\[\eta = S(\zeta), \zeta \in I_{\zeta}, \label{6.10}\]
Ця крива має три важливі властивості.
Він проходить через початок, тобто S (0) = 0.
Він дотичний до\(E^s\) біля початку, т\(\frac{dS}{d\zeta} (0) = 0\). Е.
Це локально інваріантно в тому сенсі, що будь-яка траєкторія, що починається на кривій, наближається до початку з експоненціальною швидкістю як\(t \rightarrow \infty\), і вона залишає\(B_{\epsilon}\) як\(t \rightarrow -\infty\).
Більш того, крива, що задовольняє цим трьом властивостям, унікальна. З цих причин цю криву називають локальним стабільним многовидом походження, і позначається вона:
\[W_{loc}^{s}((0, 0)) = \{(\zeta, \eta) \in B_{\epsilon}|\eta = S(\zeta)\}. \label{6.11}\]
Аналогічно існує ще одна\(C^{r}\) крива, задана графіком функції\(\eta\) змінних:
\[\zeta = U(\eta), \eta \in I_{\eta}, \label{6.12}\]
Ця крива має три важливі властивості.
Вона проходить через початок, тобто U (0) = 0.
Він дотичний до\(E^u\) біля початку, т\(\frac{dU}{d\eta} (0) = 0\). Е.
Це локально інваріантно в тому сенсі, що будь-яка траєкторія, що починається на кривій, наближається до початку з експоненціальною швидкістю як\(t \rightarrow -\infty\), і вона залишає\(B_{\epsilon}\) як\(t \rightarrow \infty\).
З цих причин цю криву називають локальним нестабільним многовидом походження, і позначається вона:
\[W_{loc}^{u}((0, 0)) = \{(\zeta, \eta) \in B_{\epsilon}|\zeta = S(\zeta)\}. \label{6.13}\]
Крива, що задовольняє цим трьом властивостям, унікальна.
Ці локальні стабільні та нестабільні многовиди є «насінням» для глобальних стабільних та нестабільних многовидів, які визначаються наступним чином:
\[W^{s} ((0, 0)) \equiv \bigcup_{t \le 0} \phi_{t}(W_{loc}^{s}((0, 0))), \label{6.14}\]
і
\[W^{u} ((0, 0)) \equiv \bigcup_{t \ge 0} \phi_{t}(W_{loc}^{u}((0, 0))), \label{6.15}\]
Зараз ми розглянемо ряд прикладів, що показують, як використовуються ці ідеї.
Приклад\(\PageIndex{13}\)
Розглянуто наступне автономне, нелінійне векторне поле на площині:
\(\dot{x} = x\),
\[\dot{y} = y + x^2, (x, y) \in \mathbb{R}^2. \label{6.16}\]
Це векторне поле має точку рівноваги на початку, (x, y) = (0, 0). Якобіан векторного поля, оціненого за початком, задається:
\[\begin{pmatrix} {1}&{0}\\ {0}&{-1} \end{pmatrix}. \label{6.17}\]
З цього розрахунку можна зробити висновок, що походження - гіперболічна сідлова точка. Крім того, вісь x є нестабільним підпростором для лінеаризованого векторного поля, а вісь y - стійким підпростором для лінеаризованого векторного поля.
Далі розглянемо нелінійне векторне поле (6.16). Оглядаючи, ми бачимо, що вісь y (тобто x = 0) є глобальним стабільним колектором для початку. Далі розглянемо нестійкий колектор. Розділення другого рівняння на перше рівняння в (6.16) дає:
\[\frac{\dot{y}}{\dot{x}} = \frac{dy}{dx} = -\frac{y}{x} + x. \label{6.18}\]
Це лінійне неавтономне рівняння. Розв'язок цього рівняння, що проходить через початок, дається:
\[y = \frac{x^2}{3}, \label{6.19}\]
Він також дотичний до нестабільного підпростору біля початку. Це глобальне нестабільне різноманіття.
Розбираємо це твердження далі. Легко обчислити потік, що генерується за допомогою (6.16). X-компонент може бути розв'язаний і замінений у компонент y, щоб отримати лінійне неавтономне рівняння першого порядку. Отже, потік, що генерується (6.16), задається:
\(x(t, x_{0}) = x_{0}e^t\),
\[y(t, t_{0}) = (y_{0}-\frac{x_{0}^2}{3})e^{-t}+\frac{x_{0}^2}{3}e^{2t}, \label{6.20}\]
Глобальний нестабільний многовид походження - це сукупність початкових умов, що мають властивість, що траєкторії через ці початкові умови наближаються до походження з експоненціальною швидкістю як\(t \rightarrow -\infty\). Вивчаючи дві складові (6.20), ми бачимо, що компонент x наближається до нуля, як і\(t \rightarrow -\infty\) для будь-якого вибору\(x_{0}\). Однак компонент y наближається лише до нуля,\(t \rightarrow -\infty\) ніби\(y_{0}\) і\(x_{0}\) вибирається таким чином, що
\[y_{0} = \frac{x_{0}^2}{3}, \label{6.21}\]
Звідси (6.21) є глобальним нестабільним різноманіттям походження.
Приклад\(\PageIndex{14}\)
Розглянемо наступні нелінійні автономні векторні поля на площині:
\(\dot{x} = x-x^3\),
\[\dot{y} = -y, (x, y) \in \mathbb{R}^2. \label{6.22}\]
Зауважте, що компоненти x і y розвиваються незалежно.
Точки рівноваги і якобійців, пов'язані з їх лінеаризаціями, наведені наступним чином:
\[(x, y) = (0, 0); \begin{pmatrix} {1}&{0}\\ {0}&{-1} \end{pmatrix}; saddle \label{6.23}\]
\[(x, y) = (\pm 1, 0); \begin{pmatrix} {-2}&{0}\\ {0}&{-1} \end{pmatrix}; sinks \label{6.24}\]
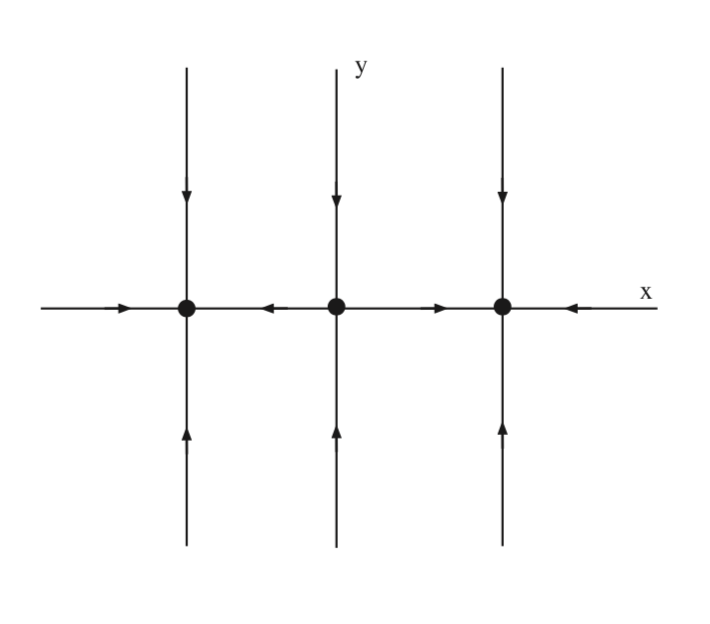
Зараз ми обчислюємо глобальні стабільні та нестабільні многовиди цих рівноваг. Починаємо з точки сідла біля початку.
\(W^{s} ((0, 0)) = \{(x, y)|x = 0\}\)
\[W^{u} ((0, 0)) = \{(x, y)|-1 < x < 1, y = 0\} \label{6.25}\]
Для раковин глобальний стабільний колектор є синонімом басейну тяжіння для раковини.
\[(1, 0): W^{s} ((1, 0)) = \{(x, y)|x > 0\} \label{6.26}\]
\[(-1, 0): W^{s} ((-1, 0)) = \{(x, y)|x < 0\} \label{6.27}\]
Приклад\(\PageIndex{15}\)
У цьому прикладі розглянуто наступне нелінійне автономне векторне поле на площині:
\(\dot{x} = -x\),
\[\dot{y} = y^{2}(1-y^{2}), (x, y) \in \mathbb{R}^2. \label{6.28}\]
Зауважте, що компоненти x і y розвиваються незалежно.
Точки рівноваги і якобійців, пов'язані з їх лінеаризаціями, наведені наступним чином:
\[(x, y) = (0, 0), (0, \pm 1) \label{6.29}\]
\[(x, y) = (0, 0); \begin{pmatrix} {-1}&{0}\\ {0}&{0} \end{pmatrix}; not hyperbolic \label{6.30}\]
\[(x, y) = (0, 1); \begin{pmatrix} {-1}&{0}\\ {0}&{-2} \end{pmatrix}; sink \label{6.31}\]
\[(x, y) = (0, -1); \begin{pmatrix} {-1}&{0}\\ {0}&{2} \end{pmatrix}; saddle \label{6.32}\]
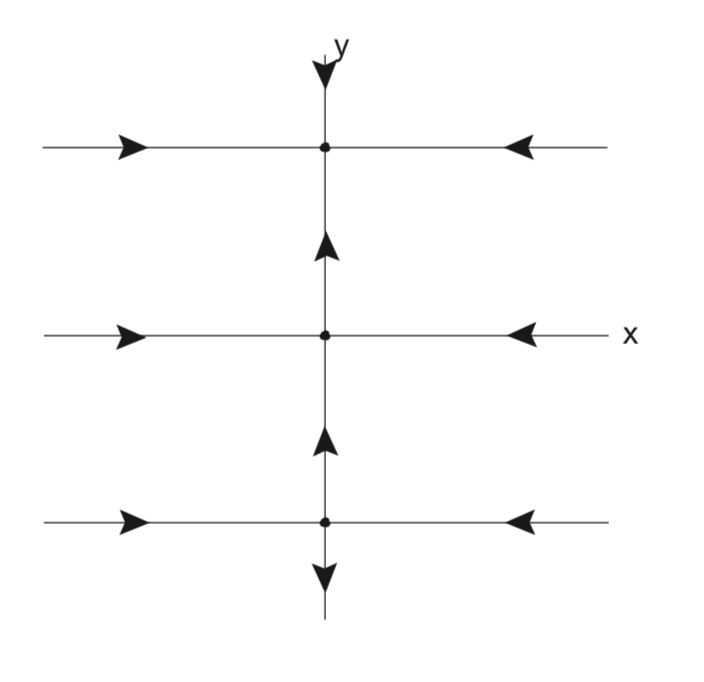
Тепер ми обчислюємо глобальну інваріантну структуру багатовидів для кожного з рівноваг, починаючи з (0, 0).
\(W^{s} ((0, 0)) = \{(x, y)|y = 0\}\)
\[W^{u} ((0, 0)) = \{(x, y)|-1 < y < 1, x = 0\} \label{6.33}\]
Вісь X - це явно глобальний стабільний колектор для цієї точки рівноваги. Відрізок на осі y між\(-1\) і 1 є інваріантним, але він не відповідає гіперболічному напрямку. Його називають центральним різноманіттям походження, і ми дізнаємося набагато більше про інваріантні многовиди, пов'язані з негіперболічними напрямками пізніше.
Точка рівноваги (0, 1) - це раковина. Його глобальний стабільний різноманіття (басейн тяжіння) дається:
\[W^{s} ((0, 1)) = \{(x, y)|y > 0\} \label{6.34}\]
Точка рівноваги\((0, -1)\) - це сідлова точка з глобальними стабільними та нестабільними многовидами, що задаються:
\(W^{s} ((0, -1)) = \{(x, y)|y = -1\}\)
\[W^{u} ((0, -1)) = \{(x, y)|-\infty < y < 0, x = 0\} \label{6.35}\]
Приклад\(\PageIndex{16}\)
У цьому прикладі розглянуто наступне нелінійне автономне векторне поле на площині:
\(\dot{x} = y\),
\[\dot{y} = x-x^{3}-\delta y, (x, y) \in \mathbb{R}^2, \delta > 0, \label{6.36}\]
\(\delta > 0\)де повинен розглядатися як параметр. Точки рівноваги задаються:
\[(x, y) = (0, 0), (\pm 1, 0). \label{6.37}\]
Ми хочемо класифікувати лінеаризовану стійкість рівноваг. Якобіан векторного поля задається:
\[A = \begin{pmatrix} {0}&{1}\\ {1-3x^2}&{-\delta} \end{pmatrix}, \label{6.38}\]
і власними значеннями якобійців є:
\[\lambda_{\pm} = -\frac{\delta}{2} \pm \frac{1}{2}\sqrt{\delta^2+4-12x^2}. \label{6.39}\]
Ми оцінюємо цей вираз для власних значень на кожному з рівноваг, щоб визначити їх лінеаризовану стійкість.
\[(0, 0); \lambda_{\pm} = -\frac{\delta}{2} \pm \frac{1}{2}\sqrt{\delta^2+4} \label{6.40}\]
Зауважте, що
\(\delta^2+4 > \delta^2\)
тому власні значення завжди дійсні і протилежного знака. Це означає, що (0, 0) є сідлом.
\[(\pm 1, 0); \lambda_{\pm} = -\frac{\delta}{2} \pm \frac{1}{2}\sqrt{\delta^2-8} \label{6.41}\]
По-перше, зверніть увагу, що
\(\delta^2-8 < \delta^2\).
Це означає, що ці дві нерухомі точки завжди є раковинами. Однак є два підвипадки.
\(\delta^2-8 < 0\): Власні значення мають ненульову уявну частину.
\(\delta^2-8 > 0\): Власні значення є чисто реальними.
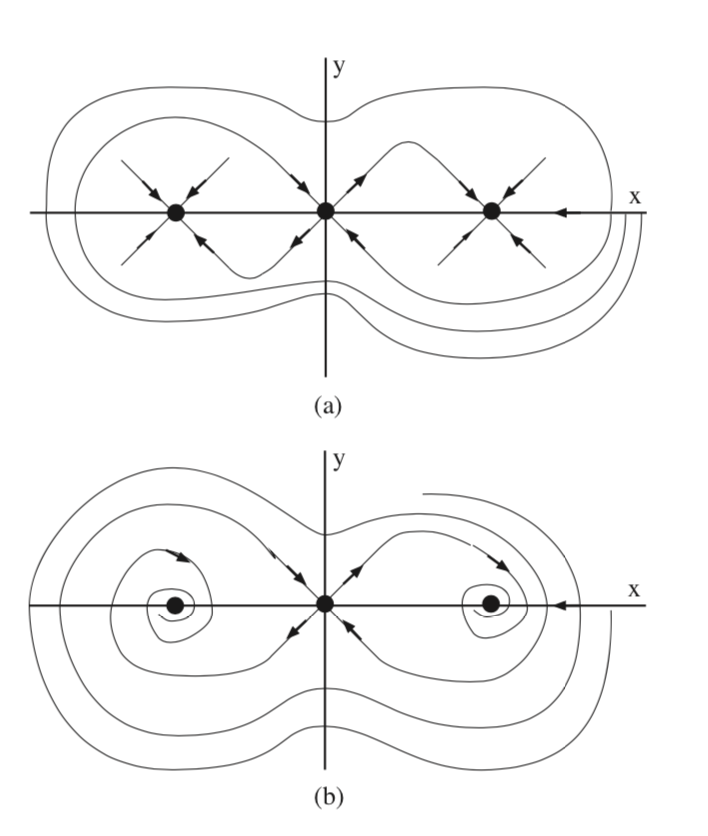
На рис. 6.4 ми накидаємо локальну інваріантну багатоподібну структуру для цих двох випадків.
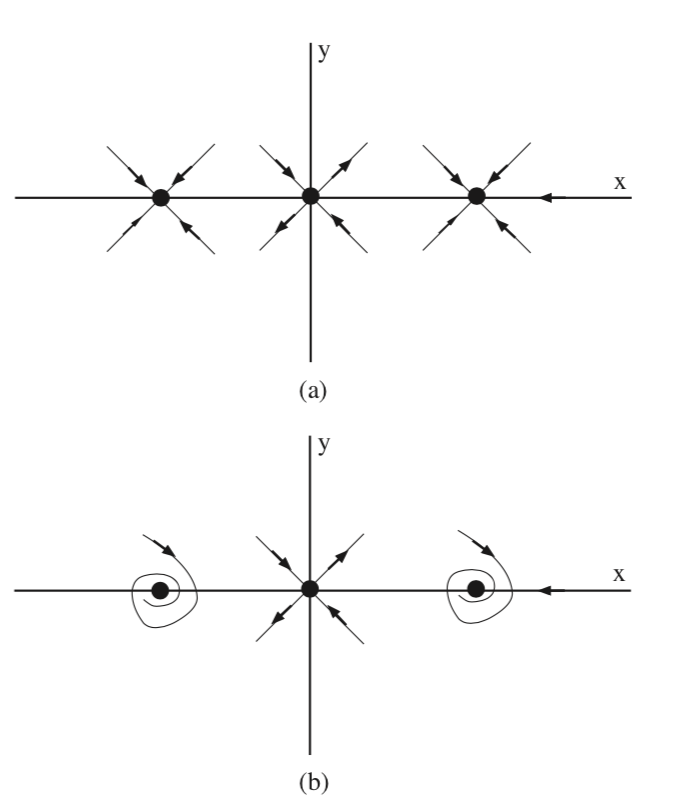
На рис. 6.5 ми намалюємо глобальну структуру інваріантного многовиду для двох випадків. У майбутніх лекціях ми дізнаємося, як можна виправдати цю цифру. Однак зверніть увагу на роль, яку відіграє стійкий колектор сідла у визначенні басейнів атракціонів двох раковин.