8.4: Функція кроку блоку
- Page ID
- 62165
У наступному розділі ми розглянемо задачі початкового значення
\[ay''+by'+cy=f(t),\quad y(0)=k_0,\quad y'(0)=k_1,\nonumber \]
де\(a\)\(b\), і\(c\) є константами і\(f\) є кусково-безперервним. У цьому розділі ми розробимо процедури використання таблиці перетворень Лапласа для пошуку перетворень Лапласа кусково-неперервних функцій та пошуку кусково-неперервних обертань перетворень Лапласа.
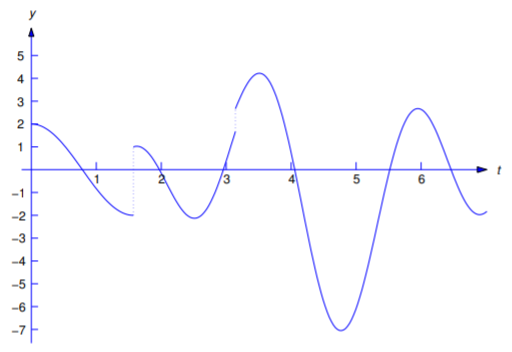
Використовуйте таблицю перетворень Лапласа, щоб знайти перетворення Лапласа
\[\label{eq:8.4.1} f(t)=\left\{\begin{array}{cl} 2t+1,&0\le t<2,\\[4pt]3t,&t\ge2 \end{array}\right.\]
(Рисунок Template:index).
Рішення
Так як формула для\(f\) змін на\(t=2\), пишемо
\[\label{eq:8.4.2} \begin{array}{ll} {\cal L}(f)&= \int_0^\infty e^{-st}f(t)\,dt \\{} &= \int_0^2 e^{-st}(2t+1)\,dt+\int_2^\infty e^{-st}(3t)\,dt. \end{array}\]
Щоб зв'язати перший член з перетворенням Лапласа, ми додаємо і віднімаємо
\[\int_2^\infty e^{-st}(2t+1)\,dt \nonumber\]
в Рівняння\ ref {eq:8.4.2} для отримання
\[\label{eq:8.4.3} \begin{array}{ll} {\cal L}(f) &{= \int_0^\infty e^{-st}(2t+1)\,dt+ \int_2^\infty e^{-st}(3t-2t-1)\,dt }\\ {}&= \int_0^\infty e^{-st}(2t+1)\,dt+ \int_2^\infty e^{-st}(t-1)\,dt \\{} &{={\cal L}(2t+1) + \int_2^\infty e^{-st}(t-1) \,dt.} \end{array}\]
Щоб зв'язати останній інтеграл з перетворенням Лапласа, ми робимо зміну змінної\(x=t-2\) і перепишемо інтеграл як
\[\begin{aligned} \int_2^\infty e^{-st}(t-1)\,dt &= \int_0^\infty e^{-s(x+2)}(x+1)\,dx \\[4pt] &=e^{-2s}\int_0^\infty e^{-sx}(x+1)\,dx.\end{aligned}\nonumber\]
Оскільки символ, який використовується для змінної інтеграції, не впливає на значення певного інтеграла, тепер ми можемо замінити\(x\) на більш стандартний\(t\) і записати
\[\int_2^\infty e^{-st}(t-1)\,dt =e^{-2s}\int_0^\infty e^{-st}(t+1)\,dt=e^{-2s}{\cal L}(t+1).\nonumber\]
Це і рівняння\ ref {eq:8.4.3} означають, що
\[{\cal L}(f)={\cal L}(2t+1)+e^{-2s}{\cal L} (t+1).\nonumber\]
Тепер ми можемо використовувати таблицю перетворень Лапласа, щоб знайти це
\[{\cal L}(f)={2\over s^2}+{1\over s} +e^{-2s}\left({1\over s^2}+{1\over s}\right).\nonumber \]
Лапласа перетворення кусково-неперервних функцій
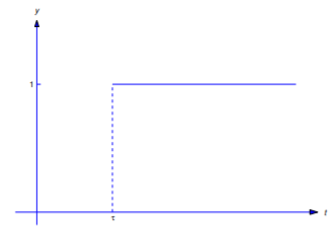
Тепер ми розробимо метод Example Template:index у систематичний спосіб знайти перетворення Лапласа кусково-неперервної функції. Зручно вводити функцію кроку одиниці, визначену як
\[\label{eq:8.4.4} u(t)=\left\{\begin{array}{rl} 0,&t<0\\ 1,&t\ge0. \end{array}\right.\]
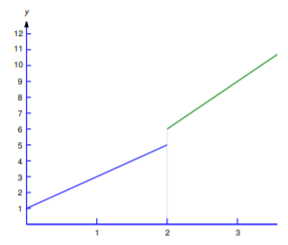
Таким чином,\(u(t)\) «крокує» від постійної величини\(0\) до постійної величини\(1\) при\(t=0\). Якщо замінити\(t\) на\(t-\tau\) в Рівняння\ ref {eq:8.4.4}, то
\[u(t-\tau)=\left\{\begin{array}{rl} 0,&t<\tau,\\ 1,&t\ge\tau \end{array}\right.; \nonumber\]
тобто крок тепер відбувається за адресою\(t=\tau\) (Рисунок Template:index).
Функція кроку дозволяє нам зручно представляти кусково безперервні функції. Наприклад, розглянемо функцію
\[\label{eq:8.4.5} f(t)=\left\{\begin{array}{rl} f_0(t),&0\le t<t_1,\\[4pt]f_1(t),&t\ge t_1, \end{array}\right.\]
де ми припускаємо, що\(f_0\) і\(f_1\) визначені на\([0,\infty)\), хоча вони рівні\(f\) тільки на зазначених інтервалах. Це припущення дозволяє нам переписати рівняння\ ref {eq:8.4.5} як
\[\label{eq:8.4.6} f(t)=f_0(t)+u(t-t_1)\left(f_1(t)-f_0(t)\right).\]
Щоб перевірити це, зауважте, що якщо\(t<t_1\) тоді\(u(t-t_1)=0\) і рівняння\ ref {eq:8.4.6} стає
\[f(t)=f_0(t)+(0)\left(f_1(t)-f_0(t)\right)=f_0(t). \nonumber\]
Якщо\(t\ge t_1\) тоді\(u(t-t_1)=1\) і рівняння\ ref {eq:8.4.6} стає
\[f(t)=f_0(t)+(1)\left(f_1(t)-f_0(t)\right)=f_1(t). \nonumber\]
Нам потрібна наступна теорема, щоб показати, як Equation\ ref {eq:8.4.6} можна використовувати для пошуку\({\cal L}(f)\).
\(g\)Дозволяти визначатися на\([0,\infty).\) Припустимо\(\tau\ge0\) і\({\cal L}\left(g(t+\tau)\right)\) існує для\(s>s_0.\) Тоді\({\cal L}\left(u(t-\tau)g(t)\right)\) існує для\(s>s_0\), і
\[{\cal L}(u(t-\tau)g(t))=e^{-s\tau}{\cal L}\left(g(t+\tau)\right).\nonumber\]
- Доказ
-
За визначенням,
\[{\cal L}\left(u(t-\tau)g(t)\right)=\int_0^\infty e^{-st} u(t-\tau)g(t)\, dt.\nonumber\]
З цього і визначення того\(u(t-\tau)\),
\[{\cal L}\left(u(t-\tau)g(t)\right)=\int_0^\tau e^{-st}(0)\,dt+\int_{\tau}^\infty e^{-st}g(t)\,dt.\nonumber\]
Перший інтеграл праворуч дорівнює нулю. Введення нової змінної інтеграції\(x=t-\tau\) в другій інтегральної прибутковості
\[{\cal L}\left(u(t-\tau)g(t)\right)=\int_0^\infty e^{-s(x+\tau)}g(x+\tau)\,dx =e^{-s\tau}\int_0^\infty e^{-sx} g(x+\tau)\,dx.\nonumber\]
Зміна назви змінної інтеграції в останньому інтегралі від\(x\) до\(t\) дає
\[{\cal L}\left(u(t-\tau)g(t)\right) =e^{-s\tau}\int_0^\infty e^{-st} g(t+\tau)\,dt=e^{-s\tau}{\cal L}(g(t+\tau)).\nonumber\]
Знайти\[{\cal L}\left(u(t-1)(t^2+1)\right).\nonumber\]
Рішення
Ось\(\tau=1\) і\(g(t)=t^2+1\), так
\[g(t+1)=(t+1)^2+1=t^2+2t+2.\nonumber\]
Так як
\[{\cal L}\left(g(t+1)\right)={2\over s^3}+{2\over s^2}+{2\over s},\nonumber\]
Теорема Template:index означає, що
\[{\cal L}\left(u(t-1)(t^2+1)\right) =e^{-s}\left({2\over s^3}+{2\over s^2}+{2\over s}\right).\nonumber\]
Використовуйте теорему Template:index, щоб знайти перетворення Лапласа функції
\[f(t)=\left\{\begin{array}{cl} 2t+1,&0\le t<2,\\[4pt]3t,&t\ge2, \end{array}\right. \nonumber\]
з Прикладу Template:index.
Рішення
Спочатку запишемо\(f\) у вигляді Рівняння\ ref {eq:8.4.6} як
\[f(t)=2t+1+u(t-2)(t-1). \nonumber\]
Тому
\[\begin{aligned} {\cal L}(f)&={\cal L}(2t+1) +{\cal L}\left(u(t-2)(t-1)\right)\\ &={\cal L}(2t+1) +e^{-2s}{\cal L}(t+1)\quad\mbox{ (from Theorem }\PageIndex{1})\\ &={2\over s^2}+{1\over s}+e^{-2s}\left({1\over s^2}+{1\over s}\right),\end{aligned}\nonumber\]
який є результатом, отриманим у прикладі Template:index.
Формула Рівняння\ ref {eq:8.4.6} може бути розширена на більш загальні кусково неперервні функції. Наприклад, ми можемо написати
\[f(t)=\left\{\begin{array}{rl} f_0(t),&0\le t<t_1,\\[4pt]f_1(t),&t_1\le t<t_2,\\[4pt]f_2(t),&t\ge t_2, \end{array}\right.\nonumber\]
як
\[f(t)=f_0(t)+u(t-t_1)\left(f_1(t)-f_0(t)\right)+ u(t-t_2)\left(f_2(t)-f_1(t)\right) \nonumber\]
\(f_0\)if\(f_1\), і\(f_2\) всі визначені на\([0,\infty)\).
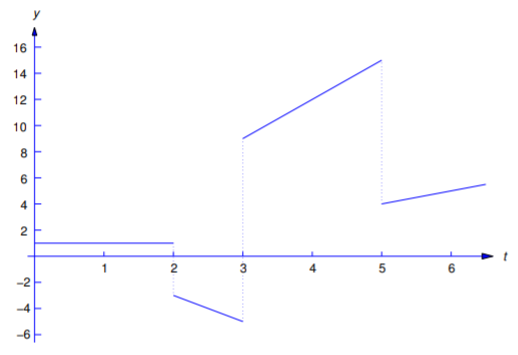
Знайдіть перетворення Лапласа
\[\label{eq:8.4.7} f(t)=\left\{\begin{array}{cl} 1,&0\le t<2,\\[4pt]-2t+1,&2\le t<3,\\[4pt]3t,&3\le t<5,\\[4pt]t-1,&t\ge5 \end{array}\right.\]
(Рисунок Template:index).
Рішення
Що стосується крокових функцій,
\[\begin{aligned} f(t)&=1+u(t-2)(-2t+1-1)+u(t-3)(3t+2t-1)\\ &= +u(t-5)(t-1-3t),\end{aligned}\nonumber\]
або
\[f(t)=1-2u(t-2)t+u(t-3)(5t-1)-u(t-5)(2t+1). \nonumber\]
Тепер теорема Template:index передбачає, що
\[\begin{aligned} {\cal L}(f)&={\cal L}(1)-2e^{-2s}{\cal L}(t+2)+e^{-3s}{\cal L}\left(5(t+3)-1\right)-e^{-5s}{\cal L}\left(2(t+5)+1\right)\\[4pt]&={\cal L}(1)-2e^{-2s}{\cal L}(t+2)+e^{-3s}{\cal L}(5t+14)-e^{-5s}{\cal L}(2t+11)\\[4pt]&={1\over s}-2e^{-2s}\left({1\over s^2}+{2\over s}\right)+ e^{-3s}\left({5\over s^2}+{14\over s}\right)-e^{-5s}\left({2\over s^2}+{11\over s}\right). \end{aligned}\nonumber\]
Тригонометричні тотожності
\[\label{eq:8.4.8} \sin (A+B)=\sin A\cos B+\cos A\sin B\]
\[\label{eq:8.4.9} \cos (A+B)=\cos A\cos B-\sin A\sin B\]
корисні в задачах, які передбачають зсув аргументів тригонометричних функцій. Ми будемо використовувати ці посвідчення в наступному прикладі.
Знайдіть перетворення Лапласа
\[\label{eq:8.4.10} f(t)=\left\{\begin{array}{cl}{\sin t,}&{0\leq t<\frac{\pi }{2}}\\{\cos t-3\sin t,}&{\frac{\pi }{2}\leq t<\pi }\\{3\cos t,}&{t\geq \pi} \end{array} \right.\]
(Рисунок Template:index).
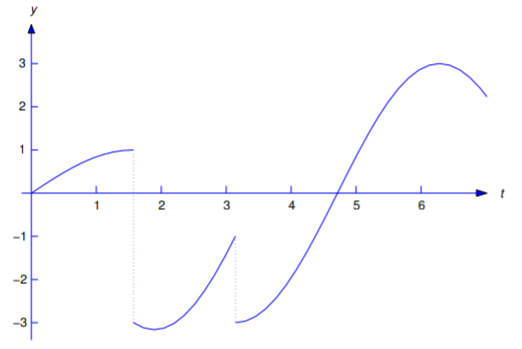
Рішення
Що стосується крокових функцій,
\[f(t)=\sin t+u(t-\pi/2) (\cos t-4\sin t)+u(t-\pi) (2 \cos t+3\sin t). \nonumber\]
Тепер теорема Template:index передбачає, що
\[\label{eq:8.4.11} \begin{array}{ccl} {\cal L}(f)&=&{\cal L}(\sin t)+e^{-{\pi\over 2}s}{\cal L} \left(\cos\left(t+{\pi\over2}\right)-4\sin\left(t+{\pi\over2}\right)\right) \\[4pt]&&\qquad+e^{-\pi s}{\cal L}\left(2\cos(t+\pi)+3\sin(t+\pi)\right). \end{array}\]
Так як
\[\cos\left(t+{\pi\over 2}\right)-4\sin\left(t+{\pi\over 2}\right)=-\sin t-4\cos t \nonumber\]
і
\[2\cos (t+\pi)+3\sin (t+\pi)=-2\cos t-3\sin t, \nonumber\]
ми бачимо з Рівняння\ ref {eq:8.4.11} що
\[\begin{align*} {\cal L}(f)&={\cal L}(\sin t)-e^{-\pi s/2}{\cal L}(\sin t+4\cos t) -e^{-\pi s}{\cal L}(2\cos t+3\sin t)\\[4pt]&={1\over s^2+1}-e^{-{\pi\over 2}s}\left({1+4s\over s^2+1}\right) -e^{-\pi s}\left({3+2s\over s^2+1}\right). \end{align*}\nonumber\]
Друга теорема про зсув
Заміна\(g(t)\)\(g(t-\tau)\) на теорему Template:index дає наступну теорему.
Якщо\(\tau\ge0\) і\({\cal L}(g)\) існує для,\(s>s_0\) то\({\cal L}\left(u(t-\tau)g(t-\tau)\right)\) існує для\(s>s_0\) і
\[{\cal L}(u(t-\tau)g(t-\tau))=e^{-s\tau}{\cal L}(g(t)),\nonumber\]
або, рівнозначно,
\[\label{eq:8.4.12} \mbox{if } g(t)\leftrightarrow G(s),\mbox{ then }u(t-\tau)g(t-\tau)\leftrightarrow e^{-s\tau}G(s).\]
Нагадаємо, що перша теорема зсуву (теорема 8.1.3) стверджує, що множення функції на\(e^{at}\) відповідає зміщенню аргументу її перетворення на одиниці. Теорема Template:index стверджує, що множення перетворення Лапласа на експоненціальне\(e^{−\tau s}\) відповідає зміщенню аргументу оберненого перетворення на\(\tau \) одиниці.
Використовуйте рівняння\ ref {eq:8.4.12} для пошуку
\[{\cal L}^{-1}\left(e^{-2s}\over s^2\right). \nonumber\]
Рішення
Щоб застосувати Рівняння\ ref {eq:8.4.12} ми дозволимо\(\tau=2\) і\(G(s)=1/s^2\). Тоді\(g(t)=t\) і рівняння\ ref {eq:8.4.12} означає, що
\[{\cal L}^{-1}\left(e^{-2s}\over s^2\right)=u(t-2)(t-2).\nonumber\]
Знайти обернене перетворення\(h\) Лапласа
\[H(s)={1\over s^2}-e^{-s}\left({1\over s^2}+{2\over s}\right)+ e^{-4s}\left({4\over s^3}+{1\over s}\right),\nonumber\]
і знайти різні формули для\(h\) відповідних інтервалів.
Рішення
Нехай
\[G_0(s)={1\over s^2},\quad G_1(s)={1\over s^2}+{2\over s},\quad G_2(s)={4\over s^3}+{1\over s}.\nonumber\]
Тоді
\[g_0(t)=t,\; g_1(t)=t+2,\; g_2(t)=2t^2+1.\nonumber\]
Отже, рівняння\ ref {eq:8.4.12} і лінійність\({\cal L}^{-1}\) означають, що
\[\begin{aligned} h(t)&={\cal L}^{-1}\left(G_0(s)\right)-{\cal L}^{-1}\left(e^{-s}G_1(s)\right)+{\cal L}^{-1}\left(e^{-4s}G_2(s)\right)\\[4pt]&=t-u(t-1)\left[(t-1)+2\right]+u(t-4)\left[2(t-4)^2+1\right]\\[4pt]&=t-u(t-1)(t+1)+u(t-4)(2t^2-16t+33),\end{aligned}\nonumber\]
який також може бути записаний як
\[h(t)=\left\{\begin{array}{cl} t,&0\le t<1,\\[4pt]-1,&1\le t<4,\\[4pt]2t^2-16t+32,&t\ge4. \end{array}\right.\nonumber \]
Знайти обернене перетворення
\[H(s)={2s\over s^2+4}-e^{-{\pi\over 2}s} {3s+1\over s^2+9}+e^{-\pi s}{s+1\over s^2+6s+10}. \nonumber\]
Рішення
Нехай
\[G_0(s)={2s\over s^2+4},\quad G_1(s)=-{(3s+1)\over s^2+9},\nonumber\]
і
\[G_2(s)={s+1\over s^2+6s+10}={(s+3)-2\over (s+3)^2+1}.\nonumber\]
Тоді
\[g_0(t)=2\cos 2t,\quad g_1(t)=-3\cos 3t-{1\over 3}\sin 3t,\nonumber\]
і
\[g_2(t)=e^{-3t}(\cos t-2\sin t).\nonumber\]
Тому рівняння\ ref {eq:8.4.12} і лінійність\({\cal L}^{-1}\) припускають, що
\[\begin{aligned} h(t)&=2\cos 2t-u(t-\pi/2)\left[3\cos 3(t-\pi/2)+{1\over 3}\sin 3\left(t-{\pi\over 2}\right)\right]\\[4pt] &= +u(t-\pi)e^{-3(t-\pi)}\left[\cos (t-\pi)-2\sin (t-\pi)\right].\end{aligned}\nonumber\]
Використовуючи тригонометричні тотожності Equation\ ref {eq:8.4.8} та Equation\ ref {eq:8.4.9}, ми можемо переписати це як
\[\label{eq:8.4.13} \begin{align} h(t)&=2\cos 2t+u(t-\pi/2)\left(3\sin 3t- {1\over 3}\cos 3t\right) \\[4pt] &= -u(t-\pi)e^{-3(t-\pi)} (\cos t-2\sin t) \end{align}\]
(Рисунок Template:index).