2.4: Перетворення нелінійних рівнянь у роздільні рівняння
- Page ID
- 62342
У розділі 2.1 виявлено, що розв'язки лінійного неоднорідного рівняння
\[y'+p(x)y=f(x)\nonumber \]
мають вигляд\(y=uy_1\), де\(y_1\) є нетривіальним розв'язком комплементарного рівняння
\[\label{eq:2.4.1} y'+p(x)y=0\]
і\(u\) є рішенням
\[u'y_1(x)=f(x).\nonumber \]
Зверніть увагу, що це останнє рівняння є роздільним, оскільки його можна переписати як
\[u'={f(x)\over y_1(x)}.\nonumber \]
У цьому розділі ми розглянемо нелінійні диференціальні рівняння, які не є роздільними для початку, але можуть бути розв'язані аналогічним чином шляхом написання їх розв'язків у вигляді\(y=uy_1\), де\(y_1\) є відповідним чином обрана відома функція і\(u\) задовольняє відокремлюване рівняння. Ми скажемо в цьому випадку, що ми перетворили дане рівняння в роздільне рівняння.
Рівняння Бернуллі
Рівняння Бернуллі - рівняння виду
\[\label{eq:2.4.2} y'+p(x)y=f(x)y^r,\]
де\(r\) може бути будь-яке дійсне число, крім\(0\) або\(1\). (Зверніть увагу, що рівняння\ ref {eq:2.4.2} є лінійним тоді і тільки тоді,\(r=0\) коли або\(r=1\).) Ми можемо перетворити рівняння\ ref {eq:2.4.2} у роздільне рівняння шляхом зміни параметрів: якщо\(y_1\) є нетривіальним розв'язком Рівняння\ ref {eq:2.4.1}, підставляючи\(y=uy_1\) в Рівняння\ ref {eq:2.4.2} дає
\[u'y_1+u(y_1'+p(x)y_1)=f(x)(uy_1)^r,\nonumber \]
що еквівалентно роздільному рівнянню
\[u'y_1(x)=f(x)\left(y_1(x)\right)^ru^r \quad \text{or} \quad {u'\over u^r}=f(x)\left(y_1(x)\right)^{r-1},\nonumber \]
так як\(y_1'+p(x)y_1=0\).
Розв'яжіть рівняння Бернуллі
\[\label{eq:2.4.3} y'-y=xy^2.\]
Оскільки\(y_1=e^x\) є розв'язком\(y'-y=0\), ми шукаємо розв'язки рівняння\ ref {eq:2.4.3} у вигляді\(y=ue^x\), де
\[u'e^x=xu^2e^{2x} \quad \text{or equivalently} \quad u'=xu^2e^x. \nonumber\]
Поділ змінних дає
\[{u'\over u^2}=xe^x, \nonumber\]
та інтеграція врожайності
\[-{1\over u}=(x-1)e^x+c. \nonumber\]
Отже,
\[u=-{1\over(x-1)e^x+c} \nonumber\]
і
\[y=-{1\over x-1+ce^{-x}}. \nonumber\]
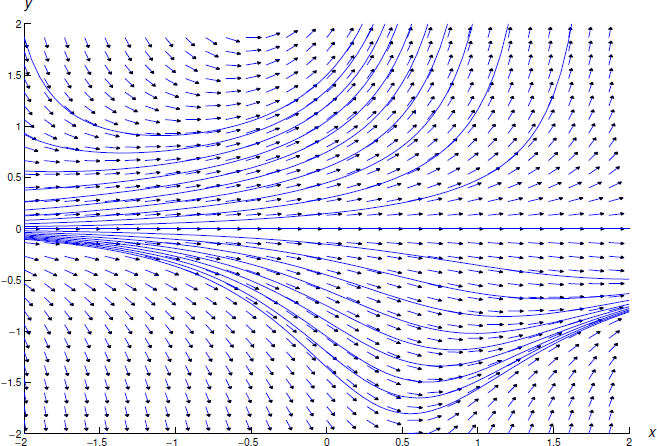
На малюнку Template:index показано поле напряму та деякі інтегральні криві рівняння\ ref {eq:2.4.3}.
Інші нелінійні рівняння, які можуть бути перетворені в роздільні рівняння
Ми бачили, що нелінійне рівняння Бернуллі може бути перетворено на відокремлене рівняння шляхом підстановки,\(y=uy_1\) якщо\(y_1\) воно обрано відповідним чином. Тепер знайдемо достатню умову для нелінійного диференціального рівняння першого порядку.
\[\label{eq:2.4.4} y'=f(x,y)\]
трансформуватися в роздільне рівняння таким же чином. Підстановка\(y=uy_1\) в рівняння\ ref {eq:2.4.4} дає
\[u'y_1(x)+uy_1'(x)=f(x,uy_1(x)),\nonumber \]
що еквівалентно
\[\label{eq:2.4.5} u'y_1(x)=f(x,uy_1(x))-uy_1'(x).\]
Якщо
\[f(x,uy_1(x))=q(u)y_1'(x)\nonumber \]
для деякої функції\(q\), тоді рівняння\ ref {eq:2.4.5} стає
\[\label{eq:2.4.6} u'y_1(x)=(q(u)-u)y_1'(x),\]
який є роздільним. Після перевірки постійних розв'язків\(u\equiv u_0\) таким чином\(q(u_0)=u_0\), ми можемо розділити змінні для отримання
\[{u'\over q(u)-u}={y_1'(x)\over y_1(x)}. \nonumber\]
Однорідні нелінійні рівнян
У тексті ми розглянемо тільки найбільш широко вивчений клас рівнянь, для яких працює метод попереднього пункту. Інші типи рівнянь з'являються у Вправи Template:index - Template:index.
Диференціальне рівняння Equation\ ref {eq:2.4.4} вважається однорідним, якщо\(x\) і\(y\) відбувається таким чином, що\(f(x,y)\) залежить тільки від співвідношення\(y/x\); тобто Equation\ ref {eq:2.4.4} може бути записано як\(f\)
\[\label{eq:2.4.7} y'=q(y/x),\]
де\(q=q(u)\) - функція однієї змінної. Наприклад,
\[y'={y+xe^{-y/x}\over x}={y\over x}+e^{-y/x}\nonumber \]
і
\[y'={y^2+xy-x^2\over x^2}=\left(y\over x\right)^2+{y\over x} -1\nonumber \]
мають вигляд Рівняння\ ref {eq:2.4.7}, з
\[q(u)=u+e^{-u} \quad \text{and} \quad q(u)=u^2+u-1,\nonumber \]
відповідно. Загальний метод, розглянутий вище, може бути застосований до Equation\ ref {eq:2.4.7} з\(y_1=x\) (і тому\(y_1'=1)\). Таким чином, підстановка\(y=ux\) в рівнянні\ ref {eq:2.4.7} дає
\[u'x+u=q(u),\nonumber \]
і поділ змінних (після перевірки постійних розв'язків\(u\equiv u_0\) таких, що\(q(u_0)=u_0\)) дає
\[{u'\over q(u)-u}={1\over x}.\nonumber \]
Перш ніж перейти до прикладів, ми вказуємо на те, що ви, можливо, вже помітили: визначення однорідного рівняння, наведене тут, не те саме, що визначення, наведене в розділі 2.1, де ми сказали, що лінійне рівняння форми
\[y'+p(x)y=0\nonumber \]
однорідна. Ми не вибачаємося за цю невідповідність, оскільки ми не створили її історично, однорідна була використана в цих двох суперечливих способах. Найважливішим є той, що стосується лінійних рівнянь. Це єдиний розділ книги, де буде застосовано значення, визначене тут.
Оскільки\(y/x\) загалом не визначено if\(x=0\), ми розглянемо розв'язки неоднорідних рівнянь тільки на відкритих інтервалах, які не містять точки\(x=0\).
Вирішити
\[\label{eq:2.4.8} y'={y+xe^{-y/x}\over x}.\]
Підстановка\(y=ux\) в рівняння\ ref {eq:2.4.8} дає
\[u'x+u = {ux+xe^{-ux/x}\over x} = u+e^{-u}. \nonumber\]
Спрощення та розділення змінних дає
\[e^uu'={1\over x}. \nonumber\]
Інтеграція врожайності\(e^u=\ln |x|+c\). Тому\(u=\ln(\ln|x|+c)\) і\(y=ux=x \ln (\ln |x|+c)\).
На малюнку Template:index показано поле напряму та інтегральні криві для Equation\ ref {eq:2.4.8}.

а. вирішити
\[\label{eq:2.4.9} x^2y'=y^2+xy-x^2.\]
b Вирішити початкову задачу значення
\[\label{eq:2.4.10} x^2y'=y^2+xy-x^2, \quad y(1)=2.\]
Рішення a
Спочатку ми знаходимо розв'язки Equation\ ref {eq:2.4.9} на відкритих інтервалах, які не містять\(x=0\). Ми можемо переписати рівняння\ ref {eq:2.4.9} як
\[y'={y^2+xy-x^2\over x^2} \nonumber\]
бо\(x\) в будь-який такий проміжок. заміщення\(y=ux\) врожайності
\[u'x+u ={ (ux)^2+x(ux)-x^2 \over x^2} = u^2+u-1,\nonumber\]
тому
\[\label{eq:2.4.11} u'x=u^2-1.\]
При огляді це рівняння має постійні розчини\(u\equiv1\) і\(u\equiv-1\). Тому\(y=x\) і\(y=-x\) є розв'язками Рівняння\ ref {eq:2.4.9}. Якщо\(u\) є розв'язком Equation\ ref {eq:2.4.11}, який не приймає значення\(\pm 1\) на деякому інтервалі, розділення змінних дає
\[{u'\over u^2-1}={1\over x},\nonumber\]
або, після часткового розширення дробу,
\[{1\over 2}\left[{1\over u-1}-{1\over u+1}\right]u'= {1\over x}.\nonumber\]
Множення на 2 та інтеграція врожайності
\[\ln\left|u-1\over u+1\right| =2 \ln |x|+k,\nonumber\]
або
\[\left|{u-1\over u+1}\right|=e^kx^2,\nonumber\]
який тримає, якщо
\[\label{eq:2.4.12} {u-1\over u+1}=cx^2 \]
де\(c\) - довільна константа. Рішення для\(u\) врожайності
\[u ={1+cx^2\over 1-cx^2}.\nonumber \]
Тому
\[\label{eq:2.4.13} y=ux={x(1+cx^2)\over 1-cx^2}\]
є розв'язком рівняння\ ref {eq:2.4.10} для будь-якого вибору константи\(c\). Встановлення\(c=0\) в Рівняння\ ref {eq:2.4.13} дає рішення\(y=x\). Однак рішення не\(y=-x\) може бути отримано з Equation\ ref {eq:2.4.13}. Таким чином, розв'язками Рівняння\ ref {eq:2.4.9} на інтервалах, які не містять,\(x=0\) є\(y=-x\) і функції виду Equation\ ref {eq:2.4.13}.
Ситуація складніше\(x=0\), якщо відкритий інтервал. По-перше, зауважте, що\(y=-x\) задовольняє рівняння\ ref {eq:2.4.9} на\((-\infty,\infty)\). Якщо\(c_1\) і\(c_2\) є довільними константами, функція
\[\label{eq:2.4.14}y=\left\{\begin{array}{ll} {\frac{x(1+c_{1}x^{2})}{1-c_{1}x^{2}},}&{a<x<0} \\ {\frac{x(1+c_{2}x^{2}}{1-c_{2}x^{2}},}&{0\leq x<b}\end{array}\right.\]
є розв'язком рівняння\ ref {eq:2.4.9} на\((a,b)\), де
\[a=\left\{\begin{array}{cl}- {1\over\sqrt{c_1}}&\mbox{ if }c_1>0,\\ -\infty&\mbox{ if }c_1\le 0, \end{array}\right. \quad \text{and} \quad b=\left\{\begin{array}{cl} {1\over\sqrt{c_2}}&\mbox{ if }c_2>0,\\ \infty&\mbox{ if }c_2\le 0. \end{array}\right.\nonumber\]
Ми залишаємо це вам, щоб переконатися в цьому. Для цього зауважте, що якщо\(y\) є якась функція виду Equation\ ref {eq:2.4.13} то\(y(0)=0\) і\(y'(0)=1\).
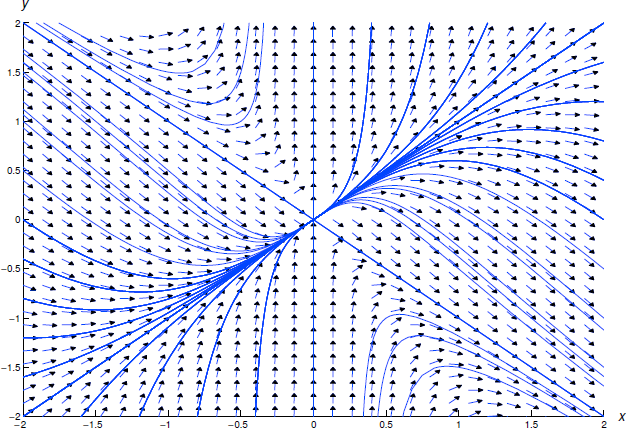
На малюнку Template:index показано поле напряму та деякі інтегральні криві для Equation\ ref {eq:2.4.9}.
Рішення б
Ми могли б отримати,\(c\) наклавши початкову умову\(y(1)=2\) в Equation\ ref {eq:2.4.13}, а потім розв'язуючи для\(c\). Однак простіше використовувати Equation\ ref {eq:2.4.12}. Так як\(u=y/x\), початкова умова\(y(1)=2\) має на увазі це\(u(1)=2\). Підставляючи це в рівняння\ ref {eq:2.4.12} дає\(c=1/3\). Отже, розв'язок Рівняння\ ref {eq:2.4.10} є
\[y={x(1+x^2/3)\over 1-x^2/3}.\nonumber\]
Інтервал дії даного розчину становить\((-\sqrt3,\sqrt3)\). Однак найбільший інтервал, на якому Equation\ ref {eq:2.4.10} має унікальне рішення\((0,\sqrt3)\). Щоб побачити це, зверніть увагу з Equation\ ref {eq:2.4.14}, що будь-яка функція форми
\[\label{eq:2.4.15} y=\left\{\begin{array}{ll} {\frac{x(1+cx^{2})}{1-cx^{2}},}&{a<x\leq 0} \\ {\frac{x(1+x^{2}/3)}{1-x^{2}/3}}&{0\leq x<\sqrt{3}}\end{array}\right.\]
є розв'язком Рівняння\ ref {eq:2.4.10} на\((a,\sqrt3)\), де\(a=-1/\sqrt c\) if\(c>0\) або\(a=-\infty\) if\(c\le0\). Чому це не суперечить теоремі 2.3.1?
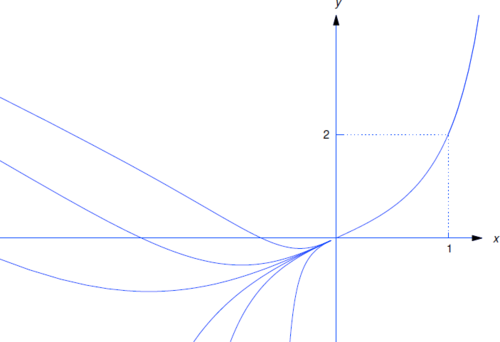
На малюнку Template:index показано декілька розв'язків початкової задачі Рівняння\ ref {eq:2.4.10}. Зверніть увагу, що ці рішення збігаються на\((0,\sqrt{3})\).
В останніх двох прикладах ми змогли вирішити задані рівняння явно. Однак це не завжди можливо, як ви переконаєтеся в вправах.
