2.3: Існування та єдиність розв'язків нелінійних рівнянь
- Page ID
- 62346
Хоча існують методи вирішення деяких нелінійних рівнянь, знайти корисні формули для розв'язків більшості неможливо. Незалежно від того, чи шукаємо ми точні розв'язки чи числові наближення, корисно знати умови, які передбачають існування та єдиність розв'язків задач початкового значення для нелінійних рівнянь. У цьому розділі ми викладемо таку умову і проілюструємо його прикладами.
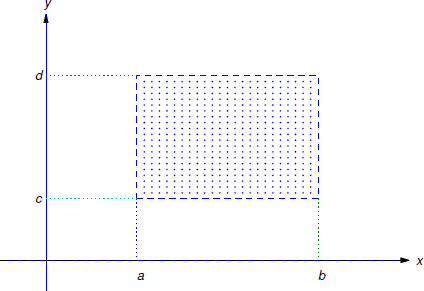
Деяка термінологія: відкритий прямокутник\(R\) - це сукупність точок,\((x,y)\) таких, що
\[a<x<b\quad\text{and}\quad c<y<d\nonumber \]
(Рисунок Template:index). Ми позначимо цей набір по\(R: \{ a < x < b, c < y < d \}\). «Відкрити» означає, що граничний прямокутник (позначений пунктирними лініями на рисунку Template:index) не включений до\(R\).
Наступна теорема дає достатні умови існування та єдиності розв'язків початкових задач для нелінійних диференціальних рівнянь першого порядку. Опускаємо доказ, який виходить за рамки цієї книги.
- Якщо\(f\) є неперервним для відкритого прямокутника\[R: \{ a < x < b, c < y < d \} \nonumber\], який містить,\((x_0,y_0)\) то початкова задача\[\label{eq:2.3.1} y'=f(x,y), \quad y(x_0)=y_0\] має принаймні один розв'язок на деякому відкритому підінтервалі\((a,b)\), який містить\(x_0.\)
- Якщо обидва\(f\) і\(f_y\) є неперервними,\(R\) то Equation\ ref {eq:2.3.1} має унікальне рішення на деякому відкритому підінтервалі\((a,b)\), який містить\(x_0\)
Важливо точно розуміти, що говорить теорема Template:index.
- (а) - теорема про існування. Це гарантує, що рішення існує на деякому відкритому інтервалі\(x_0\), який містить, але не дає інформації про те, як знайти рішення або визначити відкритий інтервал, на якому воно існує. Крім того, (a) не дає інформації про кількість розв'язків, які можуть мати Equation\ ref {eq:2.3.1}. Це залишає відкритою можливість того, що Equation\ ref {eq:2.3.1} може мати два або більше розв'язків, які відрізняються для значень\(x\) довільно близьких до\(x_0\). Ми побачимо в прикладі Template:index, що це може статися.
- (б) - теорема про єдиність. Це гарантує, що Equation\ ref {eq:2.3.1} має унікальне рішення на деякому відкритому інтервалі (a, b), який містить\(x_0\). Однак, якщо\((a,b)\ne(-\infty,\infty)\), Equation\ ref {eq:2.3.1} може мати більше одного рішення на більшому інтервалі, який містить\((a,b)\). Наприклад, може статися так, що\(b<\infty\) і всі розв'язки мають однакові значення на\((a,b)\), але два розв'язки\(y_1\) і\(y_2\) визначаються на деякому інтервалі\((a,b_1)\) з\(b_1>b\), і мають різні значення для\(b<x<b_{1}\); таким чином, графіки\(y_1\) і\(y_2\) «гілки» вимкнено» в різні боки на\(x = b\). (Див. приклад Template:index та рисунок Template:index). У цьому випадку безперервність має на увазі, що\(y_{1}(b) = y_{2}(b)\) (називають їх загальною цінністю\(y\)),\(y_{1}\) і\(y_{2}\) є обома розв'язками початкової задачі
\[\label{eq:2.3.2}y=f(x,y),\quad y(b)=\overline{y}\]
які відрізняються на кожному відкритому інтервалі, який містить\(b\). Тому\(f\) або\(f_y\) повинен мати розрив у певній точці кожного відкритого прямокутника, який містить\((b, y)\), оскільки якби це було не так,\ ref {eq:2.3.2} матиме унікальне рішення на деякому відкритому інтервалі, який містить\(b\). Ми залишаємо це вам, щоб дати подібний аналіз випадку, коли\(a > −∞\).
Розглянемо початкову задачу значення
\[\label{eq:2.3.3} y'={x^2-y^2 \over 1+x^2+y^2}, \quad y(x_0)=y_0.\]
Так як
\[f(x,y) = {x^2-y^2 \over 1+x^2+y^2} \quad \text{and} \quad f_y(x,y) = -{2y(1+2x^2)\over (1+x^2+y^2)^2} \nonumber\]
є неперервними для всіх\((x,y)\), Теорема Template:index означає, що якщо\((x_0,y_0)\) є довільним, то Equation\ ref {eq:2.3.3} має унікальне рішення на деякому відкритому інтервалі, який містить\(x_0\).
Розглянемо початкову задачу значення
\[\label{eq:2.3.4} y'={x^2-y^2 \over x^2+y^2}, \quad y(x_0)=y_0.\]
Тут
\[f(x,y) = {x^2-y^2 \over x^2+y^2}\quad \text{and} \quad f_y(x,y) = -{4x^2y \over (x^2+y^2)^2} \nonumber\]
безперервні всюди, крім в\((0,0)\). Якщо\((x_0,y_0) \ne(0,0)\), є відкритий прямокутник\(R\), який містить\((x_0,y_0)\), що не містить\((0,0)\). Оскільки\(f\) і\(f_y\) є неперервними\(R\), теорема Template:index означає, що якщо\((x_0,y_0)\ne(0,0)\) тоді Equation\ ref {eq:2.3.4} має унікальне рішення на деякому відкритому інтервалі, який містить\(x_0\).
Розглянемо початкову задачу значення
\[\label{eq:2.3.5} y'={x+y\over x-y},\quad y(x_0)=y_0.\]
Тут
\[f(x,y) = {x+y\over x-y}\quad \text{and} \quad f_y(x,y) = {2x\over (x-y)^2} \nonumber\]
безперервні скрізь, крім лінії\(y=x\). Якщо\(y_0\ne x_0\), є відкритий прямокутник\(R\), який містить\((x_0,y_0)\), що не перетинає лінію\(y=x\). Оскільки\(f\) і\(f_y\) є неперервними\(R\), теорема Template:index означає, що якщо\(y_0\ne x_0\), Equation\ ref {eq:2.3.5} має унікальне рішення на деякому відкритому інтервалі, який містить\(x_0\).
У прикладі 2.2.4 ми побачили, що рішення
\[\label{eq:2.3.6} y'=2xy^2\]
є
\[y\equiv0\quad \text{and} \quad y=-{1 \over x^2+c}, \nonumber\]
де\(c\) - довільна константа. Зокрема, це означає, що жодне рішення рівняння\ ref {eq:2.3.6} крім не\(y\equiv0\) може дорівнювати нулю для будь-якого значення\(x\). Покажіть, що теорема\(\PageIndex{1b}\) має на увазі це.
Ми отримаємо протиріччя, припускаючи, що Equation\ ref {eq:2.3.6} має рішення,\(y_1\) яке дорівнює нулю для деякого значення\(x\), але не є однаково нулем. Якщо\(y_1\) має цю властивість, є точка\(x_0\) така\(y_1(x_0)=0\), що, але\(y_1(x)\ne0\) для деякого значення\(x\) в кожному відкритому інтервалі, який містить\(x_0\). Це означає, що завдання початкового значення
\[\label{eq:2.3.7} y'=2xy^2,\quad y(x_0)=0\]
має два рішення\(y\equiv0\) і\(y=y_1\) які відрізняються для деякого значення\(x\) на кожному відкритому інтервалі, який містить\(x_0\). Це суперечить теоремі Template:index (b), оскільки в рівнянні\ ref {eq:2.3.6} функції
\[f(x,y)=2xy^2 \quad \text{and} \quad f_y(x,y)= 4xy. \nonumber\]
обидва неперервні для всіх\((x,y)\), що означає, що Equation\ ref {eq:2.3.7} має унікальне рішення на деякому відкритому інтервалі, який містить\(x_0\).
Розглянемо початкову задачу значення
\[\label{eq:2.3.8} y' = {10\over 3}xy^{2/5}, \quad y(x_0) = y_0.\]
- Для яких моментів теорема\((x_0,y_0)\)\(\PageIndex{1a}\) означає, що рівняння\ ref {eq:2.3.8} має рішення?
- Для яких моментів теорема\((x_0,y_0)\)\(\PageIndex{1b}\) означає, що Equation\ ref {eq:2.3.8} має унікальне рішення на деякому відкритому інтервалі, який містить\(x_0\)?
Рішення a
Так як
\[f(x,y) = {10\over 3}xy^{2/5} \nonumber\]
є безперервним для всіх\((x,y)\), Теорема Template:index означає, що рівняння\ ref {eq:2.3.8} має рішення для кожного\((x_0,y_0)\).
Рішення б
Тут
\[f_y(x,y) = {4 \over 3}xy^{-3/5} \nonumber\]
є безперервним для всіх\((x,y)\) с\(y\ne 0\). Отже, якщо\(y_0\ne0\) є відкритий прямокутник, на якому обидва\(f\) і\(f_y\) є неперервними, і теорема Template:index означає, що Equation\ ref {eq:2.3.8} має унікальне рішення на деякому відкритому інтервалі, який містить\(x_0\).
Якщо\(f_y(x,y)\) це не визначено,\(y=0\) а отже, переривчастий; отже, теорема Template:index не застосовується до рівняння\ ref {eq:2.3.8} якщо\(y_0=0\).
Приклад Template:index залишає відкритою можливість того, що проблема початкового значення
\[\label{eq:2.3.9} y'={10 \over 3}xy^{2/5}, \quad y(0)=0\]
має більше одного рішення на кожному відкритому інтервалі, який містить\(x_0=0\). Покажіть, що це правда.
Рішення
Шляхом огляду,\(y\equiv0\) є розв'язком диференціального рівняння
\[\label{eq:2.3.10} y'={10 \over 3} xy ^{2/5}.\]
Оскільки\(y\equiv0\) задовольняє початковій умові\(y(0)=0\), він є розв'язком Рівняння\ ref {eq:2.3.9}.
Тепер припустимо,\(y\) це рішення Equation\ ref {eq:2.3.10}, яке не є однаковим нулем. Розділення змінних у рівнянні\ ref {eq:2.3.10} дає
\[y^{-2/5}y'={10 \over 3}x \nonumber\]
на будь-якому відкритому інтервалі, де\(y\) немає нулів. Інтеграція цього і переписування довільної константи як\(5c/3\) прибутковості
\[{5\over 3}y^{3/5} = {5\over 3}(x^2+c) . \nonumber\]
Тому
\[\label{eq:2.3.11} y = (x^2+c)^{5/3}. \]
Оскільки ми розділили на\(y\) окремі змінні в Equation\ ref {eq:2.3.10}, наше виведення Equation\ ref {eq:2.3.11} є законним лише на відкритих інтервалах, де\(y\) немає нулів. Однак рівняння\ ref {eq:2.3.11} фактично визначає\(y\) для всіх\(x\), і диференціююче рівняння\ ref {eq:2.3.11} показує, що
\[\begin{aligned}y'={10 \over 3}x(x^2+c)^{2/3}={10 \over 3}xy^{2/5},\,-\infty < x < \infty\end{aligned} \]
Тому рівняння\ ref {eq:2.3.11} задовольняє рівняння\ ref {eq:2.3.10}\((-\infty,\infty)\) навіть якщо\(c\le 0\), так що\(y(\sqrt{|c|})=y(-\sqrt{|c|})=0\). Зокрема, взяття\(c=0\) в рівнянні\ ref {eq:2.3.11} дає
\[y=x^{10/3} \nonumber\]
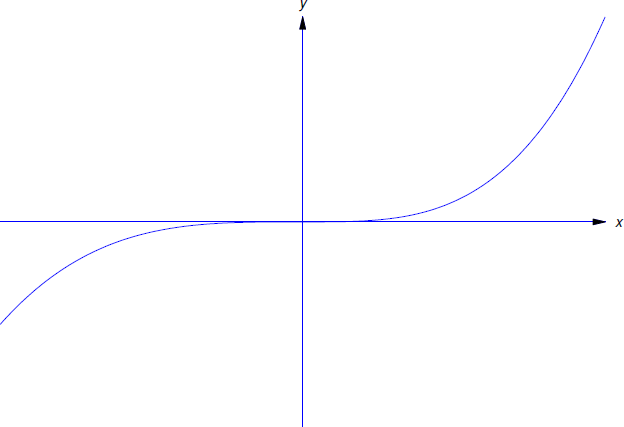
як другий розв'язок рівняння\ ref {eq:2.3.9}. Обидва рішення визначені на\((-\infty,\infty)\), і вони відрізняються на кожному відкритому інтервалі, який містить\(x_0=0\) (Рисунок Template:index). Насправді існує чотири різних розв'язки Equation\ ref {eq:2.3.9}, визначені на\((-\infty,\infty)\) які відрізняються один від одного на кожному відкритому інтервалі, який містить\(x_0=0\). Чи можете ви ідентифікувати двох інших?
З Прикладу Template:index, проблема початкового значення
\[\label{eq:2.3.12} y'={10 \over 3}xy^{2/5}, \quad y(0)=-1\]
має унікальне рішення на деякому відкритому інтервалі, який містить\(x_0=0\). Знайдіть рішення і визначте найбільший відкритий інтервал,\((a,b)\) на якому воно унікальне.
Рішення
\(y\)Дозволяти бути будь-яким розв'язком рівняння\ ref {eq:2.3.12}. Через початкову умову\(y(0)=-1\) і неперервність\(y\), існує відкритий інтервал,\(I\) який містить\(x_0=0\) на якому немає нулів, і, отже,\(y\) має вигляд Equation\ ref {eq:2.3.11}. Встановлення\(x=0\) та\(y=-1\) в рівнянні\ ref {eq:2.3.11} дає\(c=-1\), отже
\[\label{eq:2.3.13} y=(x^2-1)^{5/3}\]
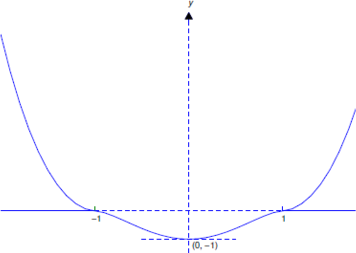
для\(x\) в\(I\). Тому кожне розв'язання рівняння\ ref {eq:2.3.12} відрізняється від нуля і задається Equation\ ref {eq:2.3.13} на\((-1,1)\); тобто Equation\ ref {eq:2.3.13} є унікальним розв'язком Рівняння\ ref {eq:2.3.12} на\((-1,1)\). Це найбільший відкритий інтервал, на якому Equation\ ref {eq:2.3.12} має унікальне рішення. Щоб побачити це, зауважте, що Equation\ ref {eq:2.3.13} є розв'язком Рівняння\ ref {eq:2.3.12} на\((-\infty,\infty)\). З вправи 2.2.15 існує нескінченно багато інших розв'язків Equation\ ref {eq:2.3.12}, які відрізняються від Equation\ ref {eq:2.3.13} на кожному відкритому інтервалі більше\((-1,1)\). Одним з таких рішень є
\[y = \left\{ \begin{array}{cl} (x^2-1)^{5/3}, & -1 \le x \le 1, \\[6pt] 0, & |x|>1. \end{array} \right. \nonumber\]
З Прикладу Template:index), проблема початкового значення
\[\label{eq:2.3.14} y'={10 \over 3}xy^{2/5}, \quad y(0)=1\]
має унікальне рішення на деякому відкритому інтервалі, який містить\(x_0=0\). Знайдіть рішення і визначте найбільший відкритий інтервал, на якому воно унікальне.
Рішення
\(y\)Дозволяти бути будь-яким розв'язком рівняння\ ref {eq:2.3.14}. Через початкову умову\(y(0)=1\) і неперервність\(y\), існує відкритий інтервал,\(I\) який містить\(x_0=0\) на якому немає нулів, і, отже,\(y\) має вигляд Equation\ ref {eq:2.3.11}. Встановлення\(x=0\) та\(y=1\) в рівнянні\ ref {eq:2.3.11} дає\(c=1\), отже
\[\label{eq:2.3.15} y=(x^2+1)^{5/3}\]
для\(x\) в\(I\). Тому кожне розв'язання рівняння\ ref {eq:2.3.14} відрізняється від нуля і задається Equation\ ref {eq:2.3.15} на\((-\infty,\infty)\); тобто Equation\ ref {eq:2.3.15} є унікальним розв'язком Рівняння\ ref {eq:2.3.14} on\((-\infty,\infty)\). Рисунок Template:index) показує графік цього розв'язку.