2.1: Лінійні рівняння першого порядку
- Page ID
- 62362
Диференціальне рівняння першого порядку вважається лінійним, якщо його можна записати як
\[\label{eq:2.1.1} y' + p(x)y = f(x).\]
Диференціальне рівняння першого порядку, яке неможливо записати так, є нелінійним. Ми говоримо, що Equation\ ref {eq:2.1.1} є однорідним, якщо\(f \equiv 0\); інакше воно неоднорідне. Так як\(y \equiv 0\), очевидно, є розв'язком однорідного рівняння
\[y' + p(x)y = 0, \nonumber\]
ми називаємо це тривіальним рішенням. Будь-яке інше рішення є нетривіальним.
Рівняння першого порядку
\[\begin{aligned} x ^ { 2 } y ^ { \prime } + 3 y & = x ^ { 2 } \\[4pt] x y ^ { \prime } - 8 x ^ { 2 } y & = \sin x \\[4pt] x y ^ { \prime } + ( \ln x ) y & = 0 \\[4pt] y ^ { \prime } & = x ^ { 2 } y - 2 \end{aligned}\]
не в формі в Equation\ ref {eq:2.1.1}, але вони лінійні, так як їх можна переписати як
\[\begin{aligned} y ^ { \prime } + \frac { 3 } { x ^ { 2 } } y & = 1 \\[4pt] y ^ { \prime } - 8 x y & = \frac { \sin x } { x } \\[4pt] y ^ { \prime } + \frac { \ln x } { x } y & = 0 \\[4pt] y ^ { \prime } - x ^ { 2 } y & = - 2 \end{aligned}\]
Ось деякі нелінійні рівняння першого порядку:
\[\begin{aligned} x y ^ { \prime } + 3 y ^ { 2 } & = 2 x & \text { (because } y \text { is squared) } \\[4pt] y y ^ { \prime } & = 3 & \text { (because of the product } y y ^ { \prime } ) \\[4pt] y ^ { \prime } + x e ^ { y } & = 12 & \text { (because of } e ^ { y } ) \end{aligned}\]
Загальний розв'язок лінійного рівняння першого порядку
Щоб мотивувати визначення, яке нам знадобиться, розглянемо просте лінійне рівняння першого порядку
\[\label{eq:2.1.2} y'={1\over x^2}.\]
З числення ми знаємо, що\(y\) задовольняє це рівняння тоді і тільки тоді, коли
\[\label{eq:2.1.3} y=-{1\over x}+c,\]
де\(c\) - довільна константа. \(c\)Викликаємо параметр і говоримо, що Equation\ ref {eq:2.1.3} визначає однопараметричне сімейство функцій. Для кожного дійсного числа функція\(c\), визначена Equation\ ref {eq:2.1.3}, є розв'язком Рівняння\ ref {eq:2.1.2} на\((-\infty,0)\) і\((0,\infty)\); крім того, кожний розв'язок Рівняння\ ref {eq:2.1.2} на будь-якому з цих інтервалів має вигляд Рівняння\ ref {eq:2.1.3} для певного вибору\(c\). Ми говоримо, що рівняння\ ref {eq:2.1.3} є загальним рішенням рівняння\ ref {eq:2.1.2}.
Ми побачимо, що подібна ситуація виникає у зв'язку з будь-яким лінійним рівнянням першого порядку.
\[\label{eq:2.1.4} y'+p(x)y=f(x);\]
тобто якщо\(p\) і\(f\) є неперервними на деякому відкритому інтервалі,\((a,b)\) то існує унікальна формула,\(y=y(x,c)\) аналогічна Equation\ ref {eq:2.1.3}, яка включає\(x\)\(c\) і параметр і має такі властивості:
- Для кожного фіксованого значення\(c\) результуючої функції\(x\) є розв'язком Рівняння\ ref {eq:2.1.4} on\((a,b)\).
- Якщо\(y\) є розв'язком Equation\ ref {eq:2.1.4} on\((a,b)\), то\(y\) його можна отримати за формулою, вибравши\(c\) відповідним чином.
Ми назвемо\(y=y(x,c)\) загальне рішення Equation\ ref {eq:2.1.4}.
Коли це буде встановлено, випливає, що рівняння форми
\[\label{eq:2.1.5} P_0(x)y'+P_1(x)y=F(x)\]
має загальне рішення на будь-якому відкритому інтервалі,\((a,b)\) на якому\(P_0\)\(P_1\), і всі неперервні і\(P_0\) не\(F\) мають нулів, оскільки в цьому випадку ми можемо переписати Equation\ ref {eq:2.1.5} у вигляді Equation\ ref {eq:2.1.4} з\(p=P_1/P_0\) і\(f=F/P_0\), які обидва неперервні на \((a,b)\).
Щоб уникнути незручних формулювань в прикладах і вправах, ми не будемо вказувати інтервал,\((a,b)\) коли ми запитуємо загальне рішення конкретного лінійного рівняння першого порядку. Погодьмося, що це завжди означає, що ми хочемо загальне рішення на кожному відкритому інтервалі, на якому\(p\) і\(f\) є неперервними, якщо рівняння має вигляд Equation\ ref {eq:2.1.4}, або на якому\(P_0\)\(P_1\), і\(F\) є неперервними і не\(P_0\) має нулів, якщо рівняння має вигляд Рівняння\ ref {eq:2.1.5}. Ми залишаємо вам визначити ці інтервали на конкретних прикладах та вправах.
Для повноти ми вказуємо\(P_0\), що якщо\(P_1\), і\(F\) всі безперервні на відкритому інтервалі\((a,b)\), але\(P_0\) мають нуль в\((a,b)\), то Equation\ ref {eq:2.1.5} може не мати загального рішення\((a,b)\) в сенсі просто визначено. Оскільки це не головний момент, який потрібно детально розробити, ми не будемо обговорювати його далі; однак див. Вправа 2.1.44 для прикладу.
Однорідні лінійні рівняння першого порядку
Почнемо з задачі пошуку загального розв'язку однорідного лінійного рівняння першого порядку. Наступний приклад нагадує знайомий результат з обчислення.
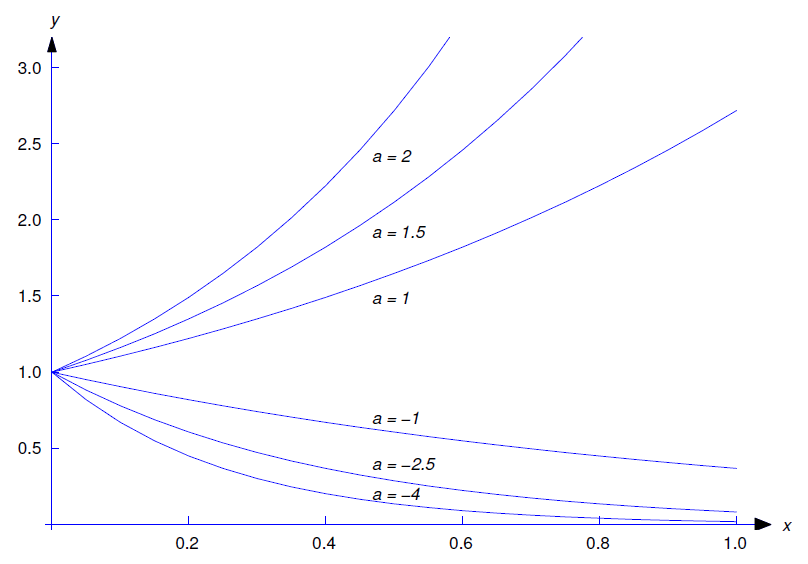
Нехай\(a\) буде постійною.
- Знайдіть загальне рішення\[y'-ay=0.\label{eq:2.1.6}\]
- Вирішити початкову задачу\[y'-ay=0,\quad y(x_0)=y_0.\nonumber \]
Рішення a
(a) Ви вже знаєте з числення, що якщо\(c\) є будь-якою константою, то\(y=ce^{ax}\) задовольняє Equation\ ref {eq:2.1.6}. Однак давайте зробимо вигляд, що ви забули про це, і використаємо цю задачу, щоб проілюструвати загальний метод розв'язання однорідного лінійного рівняння першого порядку.
Ми знаємо, що Equation\ ref {eq:2.1.6} має тривіальне рішення\(y\equiv0\). Тепер припустимо,\(y\) це нетривіальний розв'язок Рівняння\ ref {eq:2.1.6}. Тоді, оскільки диференційована функція повинна бути безперервною, повинен бути якийсь відкритий\(y\) інтервал,\(I\) на якому немає нулів. Ми переписуємо рівняння\ ref {eq:2.1.6} як
\[{y'\over y}=a \nonumber\]
для\(x\) в\(I\). Інтеграція цього показує, що
\[\ln|y|=ax+k,\quad \text{so} \quad |y|=e^ke^{ax}, \nonumber\]
де\(k\) - довільна константа. Оскільки ніколи не\(e^{ax}\) може дорівнювати нулю, не\(y\) має нулів,\(y\) тому завжди позитивний або завжди негативний. Тому ми можемо переписати\(y\) як
\[\label{eq:2.1.7} y=ce^{ax}\]
де
\[c=\left\{\begin{array}{cl}\phantom{-}e^k&\text{if} y>0, \\[4pt] -e^k&\text{if} y<0.\end{array}\right. \nonumber\]
Це показує, що кожне нетривіальне рішення Equation\ ref {eq:2.1.6} має вигляд\(y=ce^{ax}\) деякої ненульової константи\(c\). Оскільки установка\(c=0\) дає тривіальне рішення, всі розв'язки Equation\ ref {eq:2.1.6} мають вигляд Equation\ ref {eq:2.1.7}. І навпаки, рівняння\ ref {eq:2.1.7} є розв'язком рівняння\ ref {eq:2.1.6} для кожного вибору\(c\), оскільки диференціювання рівняння\ ref {eq:2.1.7} дає результат\(y'=ace^{ax}=ay\).
Рішення б
Накладення початкового стану\(y(x_0)=y_0\) дає врожайність\(y_0=ce^{ax_0}\), так\(c=y_0e^{-ax_0}\) і
\[y=y_0e^{-ax_0}e^{ax}=y_0e^{a(x-x_0)}. \nonumber\]
На малюнку Template:index показано графіки цієї функції з\(x_{0}=0\) різними значеннями\(a\).\(y_{0}=1\)
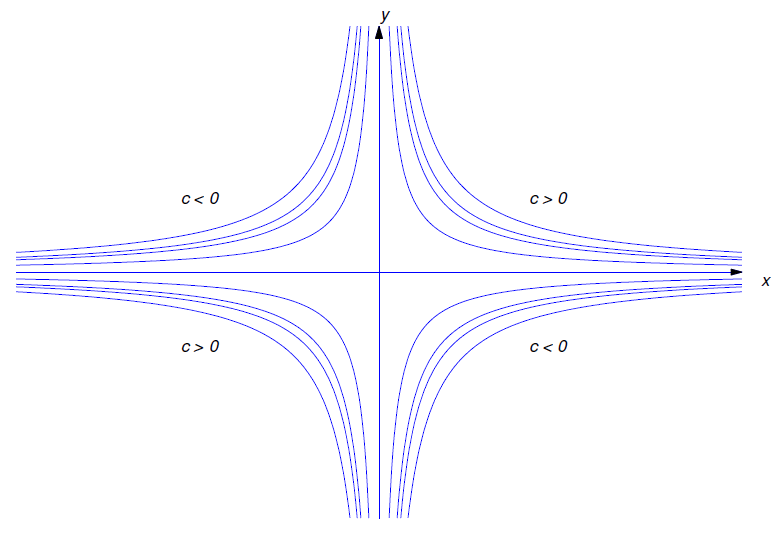
a. знайти загальне рішення
\[xy'+y=0.\label{eq:2.1.8}\]
b Вирішити початкову задачу значення
\[xy'+y=0,\quad y(1)=3.\label{eq:2.1.9}\]
Рішення a
Ми переписуємо рівняння\ ref {eq:2.1.8} як
\[\label{eq:2.1.10} y'+{1\over x}y=0,\]
де\(x\) обмежується або\((-\infty,0)\) або\((0,\infty)\). Якщо\(y\) є нетривіальним розв'язком Equation\ ref {eq:2.1.10},\(y\) має бути деякий відкритий інтервал I, на якому немає нулів. Ми можемо переписати рівняння\ ref {eq:2.1.10} як
\[{y'\over y}=-{1\over x} \nonumber\]
для\(x\) в\(I\). Інтеграція показує, що
\[\ln|y|=-\ln|x|+k,\quad so\quad|y|={e^k\over|x|}. \nonumber\]
Оскільки функція, яка задовольняє останнє рівняння, не може змінити знак ні на\((0,\infty)\) одному\((-\infty,0)\) або, ми можемо переписати цей результат простіше, як
\[\label{eq:2.1.11} y={c\over x}\]
де
\[c=\left\{\begin{array}{cl}\phantom{-}e^k&\text{if} y>0, \\[4pt] -e^k& \,\text{if} y<0.\end{array}\right. \nonumber\]
Тепер ми показали, що кожне розв'язання Equation\ ref {eq:2.1.10} задається Equation\ ref {eq:2.1.11} для певного вибору\(c\). (Незважаючи на те, що ми\(y\) припустили, що вивести Equation\ ref {eq:2.1.11} нетривіально, ми можемо отримати тривіальне рішення, встановивши\(c=0\) в Equation\ ref {eq:2.1.11}.) І навпаки, будь-яка функція виду Рівняння\ ref {eq:2.1.11} є розв'язком Рівняння\ ref {eq:2.1.10}, оскільки диференціююче рівняння\ ref {eq:2.1.11} дає
\[y'=-{c\over x^2}, \nonumber\]
і підставляючи це і рівняння\ ref {eq:2.1.11} в Рівняння\ ref {eq:2.1.10} дає
\[\begin{aligned} y'+{1\over x}y&=&-{c\over x^2}+{1\over x}{c\over x}\\[4pt] &=&-{c\over x^2}+{c\over x^2}=0.\end{aligned}\]
Рисунок Template:index показує графіки деяких розв'язків, що відповідають різним значенням\(c\)
Рішення б
Накладення початкової умови\(y(1)=3\) в Equation\ ref {eq:2.1.11} дає результат\(c=3\). Тому розв'язком рівняння\ ref {eq:2.1.9} є
\[y={3\over x}. \nonumber\]
Інтервал дії даного розчину становить\((0,\infty)\).
Результати наведені в прикладах\(\PageIndex{3a}\) і\(\PageIndex{4b}\) є окремими випадками наступної теореми.
Якщо\(p\) неперервний,\((a,b),\) то загальний розв'язок однорідного рівняння
\[\label{eq:2.1.12} y'+p(x)y=0\]
на\((a,b)\) є
\[y=ce^{-P(x)}, \nonumber\]
де
\[\label{eq:2.1.13} P(x)=\int p(x)\,dx\]
це будь-яке антипохідне\(p\) від\((a,b);\) того, що\(,\)
\[\label{eq:2.1.15} P'(x)=p(x), \quad a<x<b\]
Якщо\(y=ce^{-P(x)}\), диференціювання\(y\) та використання Equation\ ref {eq:2.1.15} показує, що
\[y'=-P'(x)ce^{-P(x)}=-p(x)ce^{-P(x)}=-p(x)y, \nonumber\]
так\(y'+p(x)y=0\); тобто\(y\) є розв'язком Рівняння\ ref {eq:2.1.12}, для будь-якого вибору\(c\).
Тепер ми покажемо, що будь-який розв'язок Equation\ ref {eq:2.1.12} може бути записаний як\(y=ce^{-P(x)}\) для певної константи\(c\). Тривіальне рішення можна записати таким чином, з\(c=0\). Тепер припустимо,\(y\) це нетривіальне рішення. Тоді є відкритий підінтервал\(I\)\((a,b)\) на який не\(y\) має нулів. Ми можемо переписати рівняння\ ref {eq:2.1.12} як
\[\label{eq:2.1.16} \frac{y'}{y}=-p(x)\]
для\(x\) в\(I\). Інтеграція рівняння\ ref {eq:2.1.16} та нагадування рівняння\ ref {eq:2.1.13} дає
\[\ln|y|=-P(x) + k, \nonumber\]
де\(k\) константа. Це означає, що
\[|y|=e^ke^{-P(x)}. \nonumber\]
Оскільки\(P\) визначається для всіх\(x\) в\((a,b)\) і експоненціальна ніколи не може дорівнювати нулю, ми можемо взяти\(I=(a,b)\), так що\(y\) має нулі на\((a,b)\)\((a,b)\), так що ми можемо переписати останнє рівняння як\(y=ce^{-P(x)}\), де
\[c=\left\{\begin{array}{cl}\phantom{-}e^k&\text{if } y>0\text{ on } (a,b),\\[4pt] -e^k&\text{if } y<0\text{ on }(a,b).\end{array}\right. \nonumber\]
ЗАУВАЖЕННЯ: Переписання диференціального рівняння першого порядку так, що одна сторона залежить тільки від,\(y\)\(y'\) а інша залежить тільки від\(x\) називається поділом змінних. Ми зробили це в прикладах Template:index і Template:index, а також у переписуванні рівняння\ ref {eq:2.1.12} і рівняння\ ref {eq:2.1.16}. Ми будемо застосовувати цей метод до нелінійних рівнянь у розділі 2.2.
Лінійні неоднорідні рівняння першого порядку
Тепер ми вирішимо неоднорідне рівняння
\[\label{eq:2.1.17} y'+p(x)y=f(x).\]
При розгляді цього рівняння ми називаємо
\[y'+p(x)y=0\nonumber \]
комплементарне рівняння.
Ми знайдемо розв'язки Equation\ ref {eq:2.1.17} у вигляді\(y=uy_1\), де\(y_1\) є нетривіальним розв'язком комплементарного\(u\) рівняння і його потрібно визначити. Цей метод використання розв'язку комплементарного рівняння для отримання розв'язків неоднорідного рівняння є окремим випадком методу, який називається варіацією параметрів, з яким ви зіткнетеся кілька разів у цій книзі. (Очевидно, що не\(u\) може бути постійним, оскільки якби це було, ліва сторона Equation\ ref {eq:2.1.17} була б нульовою. Визнаючи це, ранні користувачі цього методу розглядали\(u\) як «параметр», який змінюється; отже, назва «варіація параметрів».)
Якщо
\[y=uy_1, \quad \text{then}\quad y'=u'y_1+uy_1'.\nonumber \]
Підстановка цих виразів для\(y\) і\(y'\) в Рівняння\ ref {eq:2.1.17} дає
\[u'y_1+u(y_1'+p(x)y_1)=f(x),\nonumber \]
що зводиться до
\[\label{eq:2.1.18} u'y_1=f(x),\]
оскільки\(y_1\) є розв'язком комплементарного рівняння; тобто
\[y_1'+p(x)y_1=0.\nonumber \]
На доказ теореми 2.2.1 ми побачили, що не\(y_1\) має нулів на інтервалі, де\(p\) є безперервним. Тому ми можемо розділити рівняння\ ref {eq:2.1.18} через на\(y_1\), щоб отримати
\[u'=f(x)/y_1(x).\nonumber \]
Ми можемо інтегрувати це (вводячи константу інтеграції) та помножити результат на,\(y_1\) щоб отримати загальний розв'язок Equation\ ref {eq:2.1.17}. Перш ніж перейти до формального доказу цього позову, розглянемо кілька прикладів.
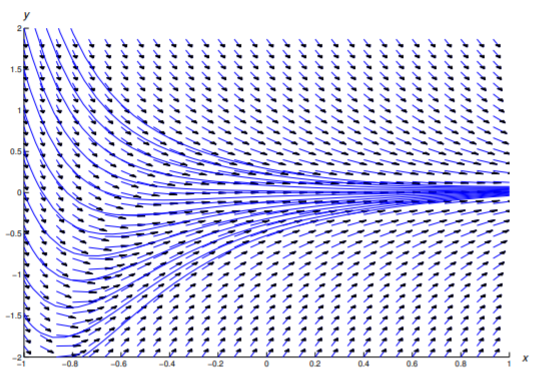
Знайдіть загальне рішення
\[\label{eq:2.1.19} y'+2y=x^3e^{-2x}.\]
Застосовуючи приклад 2.1.3 с\(a=-2\), ми бачимо, що\(y_1=e^{-2x}\) це рішення комплементарного рівняння\(y'+2y=0\). Тому ми шукаємо розв'язки рівняння\ ref {eq:2.1.19} у вигляді\(y=ue^{-2x}\), щоб
\[\label{eq:2.1.20} y'=u'e^{-2x}-2ue^{-2x}\quad \text{and} \quad y'+2y=u'e^{-2x}-2ue^{-2x}+2ue^{-2x}=u'e^{-2x}.\]
Тому\(y\) є розв'язком Рівняння\ ref {eq:2.1.19} якщо і тільки тоді
\[u'e^{-2x}=x^3e^{-2x}\quad \text{or, equivalently},\quad u'=x^3.\nonumber \]
Тому
\[u={x^4\over4}+c,\nonumber \]
і
\[y=ue^{-2x}=e^{-2x}\left({x^4\over4}+c\right)\nonumber \]
є загальним розв'язком Рівняння\ ref {eq:2.1.19}.
На малюнку Template:index показано поле напряму та деякі інтегральні криві для Equation\ ref {eq:2.1.19}.
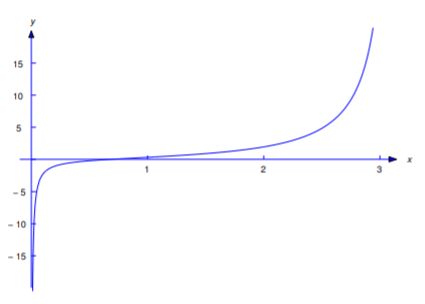
Знайдіть загальне рішення
\[\label{eq:2.1.29} y'+(\cot x)y=x\csc x.\]
Вирішити початкову задачу
\[\label{eq:2.1.30} y'+(\cot x)y=x\csc x,\quad y(\pi/2)=1.\]
Тут\(p(x)=\cot x\) і\(f(x)= x\csc x\) обидва неперервні, крім точок\(x=r\pi\), де\(r\) є ціле число. Тому ми шукаємо розв'язки рівняння\ ref {eq:2.1.29} на інтервалах\(\left(r\pi, (r+1)\pi \right)\). Потрібен нетривальний\(y_1\) розв'язок комплементарного рівняння; таким чином,\(y_1\) повинен задовольнити\(y_1'+(\cot x)y_1=0\), який ми переписуємо як
\[\label{eq:2.1.22} {y_1'\over y_1}=-\cot x=-{\cos x\over\sin x}.\]
Інтеграція цієї врожайності
\[\ln|y_1|=-\ln|\sin x|,\nonumber \]
де ми приймаємо константу інтеграції рівною нулю, оскільки нам потрібна лише одна функція, яка задовольняє Equation\ ref {eq:2.1.22}. \(y_1=1/\sin x\)Зрозуміло, що це відповідний вибір. Тому шукаємо розв'язки рівняння\ ref {eq:2.1.29} у вигляді
\[y={u\over\sin x},\nonumber \]
щоб
\[\label{eq:2.1.23} y'={u'\over\sin x}-{u\cos x\over\sin^2x}\]
і
\[\label{eq:2.1.24} \begin{array}{rcl} y'+(\cot x)y&=& {u'\over\sin x}-{u\cos x\over\sin^2x}+{u\cot x\over\sin x}\\[4pt] &=&{u'\over\sin x}-{u\cos x\over\sin^2x}+{u\cos x\over\sin^2 x}\\[4pt] &=&{u'\over\sin x}. \end{array}\]
Тому\(y\) є розв'язком Рівняння\ ref {eq:2.1.29} якщо і тільки тоді
\[u'/\sin x=x\csc x=x/\sin x\quad \text{or, equivalently,}\quad u'=x.\nonumber \]
Інтеграція цієї врожайності
\[\label{eq:2.1.25} u={x^2\over2}+c, \quad\text{ and}\quad y={u\over\sin x}= {x^2\over 2\sin x}+ {c\over\sin x}.\]
є загальним розв'язком Рівняння\ ref {eq:2.1.29} на кожному інтервалі\(\left(r\pi,(r+1)\pi\right)\) (\(r=\)ціле число).
b. накладення початкової умови\(y(\pi/2)=1\) в рівнянні\ ref {eq:2.1.25} дає
\[1={\pi^2\over 8}+c\text{ or} c=1-{\pi^2\over 8}.\nonumber \]
Таким чином,
\[y={x^2\over 2\sin x}+{(1-\pi^2/8)\over\sin x}\nonumber \]
є розв'язком Рівняння\ ref {eq:2.1.29}. Інтервал дії цього рішення дорівнює\((0,\pi)\); на малюнку 2.1.4 показаний його графік.
ЗАУВАЖЕННЯ: Не потрібно було робити обчислення\ ref {eq:2.1.23} і\ ref {eq:2.1.24} у прикладі Template:index, оскільки ми показали в попередньому прикладі 2.1.5, що якщо\(y = uy_{1}\) де\(y'_{1}+ p(x)y_{1}=0\), то\(y'+ p(x)y = u'y_{1}\). Ми зробили ці обчислення, щоб ви побачили, що це відбувається в цьому конкретному прикладі. Ми рекомендуємо включати ці «непотрібні» обчислення у виконання вправ, поки ви не впевнені, що дійсно розумієте метод. Після цього опустіть їх.
Узагальнено метод варіації параметрів для розв'язання
\[\label{eq:2.1.26} y'+p(x)y=f(x)\]
наступним чином:
a. знайти\(y_1\) таку функцію, що
\[{y_1'\over y_1}=-p(x).\nonumber \]
Для зручності візьміть константу інтеграції рівною нулю.
б. писати
\[\label{eq:2.1.27} y=uy_1\]
нагадати собі про те, що ви робите.
c. писати\(u'y_1=f\) і вирішувати для\(u'\); таким чином,\(u'=f/y_1\).
d\(u'\) Інтегрувати для отримання\(u\), з довільною константою інтеграції.
e. замінити\(u\) в рівняння\ ref {eq:2.1.27} для отримання\(y\).
Вирішити рівняння, записане як
\[P_0(x)y'+P_1(x)y=F(x),\nonumber \]
ми рекомендуємо розділити на,\(P_0(x)\) щоб отримати рівняння виду Equation\ ref {eq:2.1.26}, а потім слідувати цій процедурі.
Рішення в інтегральній формі
Іноді інтеграли, що виникають при розв'язанні лінійного рівняння першого порядку, не можуть бути оцінені через елементарні функції. В цьому випадку рішення необхідно залишити в терміні цілісного.
Знайдіть загальне рішення
\[y'-2xy=1.\nonumber \]
Вирішити початкову задачу
\[\label{eq:2.1.28} y'-2xy=1,\quad y(0)=y_0.\]
а. щоб застосувати варіацію параметрів, нам потрібно нетривіальне рішення\(y_1\) комплементарного рівняння; таким чином\(y_1'-2xy_1=0\), яке ми переписуємо як
\[{y_1'\over y_1}=2x.\nonumber \]
Інтегруючи це та приймаючи константу інтеграції нульовою прибутковістю
\[\ln|y_1|=x^2,\quad \text{so} \quad|y_1|=e^{x^2}.\nonumber \]
Вибираємо\(y_1=e^{x^2}\) і шукаємо розв'язки рівняння\ ref {eq:2.1.28} у вигляді\(y=ue^{x^2}\), де
\[u'e^{x^2}=1,\quad \text{so} \quad u'=e^{-x^2}.\nonumber \]
Тому
\[u=c+\int e^{-x^2}dx,\nonumber \]
але ми не можемо спростити інтеграл праворуч, тому що немає елементарної функції з похідною рівною\(e^{-x^2}\). Тому найкращою доступною формою для загального розв'язку Рівняння\ ref {eq:2.1.28} є
\[\label{eq:2.1.49}y=ue^{x^2}= e^{x^2}\left(c+\int e^{-x^2}dx\right).\]
b Оскільки початкова умова в Equation\ ref {eq:2.1.28} накладається на\(x_0=0\), зручно переписати Equation\ ref {eq:2.1.49} як
\[\begin{aligned}y=e^{x^2}\left(c+\int_{0}^{x}e^{-t^2}dt \right), \quad\text{since}\quad\int_{0}^{0}e^{-t^2}dt=0\end{aligned}\nonumber \]
Налаштування\(x=0\) і\(y=y_0\) тут показує, що\(c=y_0\). Тому розв'язанням початкової задачі значення є
\[\label{eq:2.1.51}y=e^{x^2}\left(y_0 +\int^x_0 e^{-t^2}dt\right).\]
Для заданого значення\(y_0\) і кожного фіксованого\(x\) інтеграл праворуч може бути оцінений числовими методами. Альтернативною процедурою є застосування процедур числового інтегрування, розглянутих у розділі 3, безпосередньо до початкової задачі Equation\ ref {eq:2.1.28}. На малюнку 2.1.5 показані графіки рівняння\ ref {eq:2.1.51} для декількох значень\(y_0\).
Теорема про існування та єдиність
Метод варіації параметрів призводить до цієї теореми.
Припустимо\(f\),\(p\) і є неперервними на відкритому інтервалі\((a,b),\) і нехай\(y_1\) буде будь-який нетривіальний розв'язок комплементарного рівняння
\[y'+p(x)y=0 \nonumber\]
на\((a,b)\). Потім:
- Загальний розв'язок неоднорідного\((a,b)\) рівняння\[\label{eq:2.1.31} y'+p(x)y=f(x)\] на\[\label{eq:2.1.32} y=y_1(x)\left(c +\int f(x)/y_1(x)\,dx\right).\]
- Якщо\(x_0\) є довільною точкою в\((a,b)\) і\(y_0\) є довільним дійсним числом,\(,\) то початкова задача\[y'+p(x)y=f(x),\quad y(x_0)=y_0\nonumber \] має унікальний розв'язок\[ y=y_1(x)\left({y_0\over y_1(x_0)} +\int^x_{x_0} {f(t)\over y_1(t)}\, dt\right)\nonumber \] на\((a,b).\)
- Доказ
-
(a) Щоб показати, що рівняння\ ref {eq:2.1.32} є загальним рішенням рівняння\ ref {eq:2.1.31} на\((a,b)\), ми повинні довести, що:
- Якщо\(c\) є будь-якою константою, функція\(y\) в Equation\ ref {eq:2.1.32} є розв'язком Рівняння\ ref {eq:2.1.31} на\((a,b)\).
- Якщо\(y\) є розв'язком Рівняння\ ref {eq:2.1.31},\((a,b)\)\(y\) то для деякої константи має вигляд Equation\ ref {eq:2.1.32}\(c\).
Щоб довести (i), ми спочатку зауважимо, що будь-яка функція виду Equation\ ref {eq:2.1.32} визначена на\((a,b)\), оскільки\(p\) і\(f\) є неперервними\((a,b)\). Диференціююче рівняння\ ref {eq:2.1.32} дає
\[y'=y_1'(x)\left(c +\int f(x)/y_1(x)\, dx\right)+f(x).\nonumber \]
Оскільки\(y_1'=-p(x)y_1\) це і рівняння\ ref {eq:2.1.32} означають, що
\[\begin{aligned} y'&=-p(x)y_1(x)\left(c +\int f(x)/y_1(x)\, dx\right)+f(x)\\[4pt] &=-p(x)y(x)+f(x),\end{aligned}\nonumber \]
що означає, що\(y\) це рішення рівняння\ ref {eq:2.1.31}.
Щоб довести (ii), припустимо,\(y\) є розв'язком Рівняння\ ref {eq:2.1.31} на\((a,b)\). З доказу теореми 2.1.1, ми знаємо, що не\(y_1\) має нулів на\((a,b)\), тому функція\(u=y/y_1\) визначається на\((a,b)\). Більш того, так як
\[y'=-py+f\quad \text{and}\quad y_1'=-py_1,\nonumber \]
\[\begin{aligned} u'&={y_1y'-y_1'y\over y_1^2} \\[4pt] &={y_1(-py+f)-(-py_1)y\over y_1^2}={f\over y_1}.\end{aligned}\nonumber \]
Інтеграція\(u'=f/y_1\) врожайності
\[u=\left(c +\int f(x)/y_1(x)\, dx\right),\nonumber \]
що має на увазі рівняння\ ref {eq:2.1.32}, так як\(y=uy_1\).
(b) Ми довели (a), де\(\int f(x)/y_1(x)\,dx\) в Equation\ ref {eq:2.1.32} є довільним антипохідним від\(f/y_1\). Тепер зручно вибрати антипохідну, яка дорівнює нулю коли\(x=x_0\), і записати загальний розв'язок Equation\ ref {eq:2.1.31} як
\[y=y_1(x)\left(c +\int^x_{x_0} {f(t)\over y_1(t)}\, dt\right). \nonumber\]
Так як
\[y(x_0)= y_1(x_0)\left(c +\int^{x_0}_{x_0} {f(t)\over y_1(t)}\, dt\right)=cy_1(x_0), \nonumber\]
ми бачимо, що\(y(x_0)=y_0\) якщо і тільки якщо\(c=y_0/y_1(x_0)\).
