3.2: Автономні рівняння першого порядку

У цьому розділі ми розглянемо методи дослідження стійкості нелінійних автономних рівнянь першого порядку. Потім ми продовжимо це дослідження до розгляду сімейств рівнянь першого порядку, які пов'язані через параметр.

Нагадаємо, що автономне рівняння першого порядку дається у вигляді

\[\dfrac{dy}{dt} = f(y). \nonumber \]

Будемо вважати, що\(f\) і\(\dfrac{\partial f}{\partial y}\) є неперервними функціями\(y\), так що ми знаємо, що рішення початкових задач значення існують і є унікальними.

Про якісних методах вивчення автономних рівнянь ми нагадаємо, розглянувши на прикладі.

\[\dfrac{d y}{d t}=y-y^{2} \label{3.3} \]

Це лише приклад логістичного рівняння.

По-перше, визначають рівноважні, або постійні, рішення, дані\(y^{\prime}= 0\). Для цього випадку у нас є\(y-y^{2}=0\). Отже, рівноважними рішеннями є\(y=0\) і\(y=1\). Намальовуючи ці рішення, ми ділимо\(t y\) -площину на три області. Рішення, що виникають в одному з цих регіонів за\(t=t_{0}\) бажанням, залишаються в цьому регіоні для всіх,\(t>t_{0}\) оскільки рішення не можуть перетинатися. [Зауважте, що якщо два рішення перетинаються, то вони мають спільні значення\(y_{1}\) в той час\(t_{1}\). Використовуючи цю інформацію, ми могли б встановити початкову задачу значення, для якої початкова умова\(y\left(t_{1}\right)=y_{1}\). Оскільки два різні розв'язки перетинаються в цій точці у фазовій площині, ми мали б задачу початкового значення з двома різними розв'язками, відповідними однаковій початковій умові. Це суперечить викладеному вище припущенню унікальності. Ми залишимо читача, щоб вивчити це далі в домашньому завданні.]

Далі визначаємо поведінку рішень в трьох регіонах. Відзначивши, що\(d y / d t\) дає нахил будь-якого рішення в площині, то виявляємо, що рішення монотонні в кожному регіоні. А саме в регіонах\(d y / d t>0\), де, ми маємо монотонно зростаючі функції. Визначаємо це з правого боку нашого рівняння.

Наприклад, в цій проблемі\(y-y^{2}>0\) тільки для середнього регіону і\(y-y^{2}<0\) для двох інших регіонів. Таким чином, ухил позитивний в середній області, даючи піднімається розчин, як показано на малюнку 3.1. Зверніть увагу, що це рішення не перетинає рівноважні рішення. Аналогічні заяви можна зробити і про рішення в інших регіонах.

Ми також відзначимо, що рішення по обидва боки\(y = 1\) схильні наближатися до цього рівноважного рішення для великих значень\(t\). Насправді, незалежно від того, наскільки близьким є\(y = 1\), врешті-решт один підійде до цього рішення як\(t → ∞\). Отже, рівноважний розчин - це стійке рішення. Точно так само ми бачимо, що\(y = 0\) це нестійке рівноважне рішення.

Якщо нас цікавить лише поведінка рівноважних розв'язків, ми могли б просто побудувати фазову лінію. На малюнку 3.2 розміщуємо вертикальну лінію праворуч від ділянки\(ty\) -plane. На цій лінії спочатку ставлять точки на відповідних рівноважних розв'язках і позначають рішення. Ці точки на рівноважних розв'язках є кінцевими точками протягом трьох інтервалів. Потім у кожному інтервалі поміщають стрілки вгору (вниз), що вказують на рішення з позитивними (негативними) нахилами. Дивлячись на фазову лінію, тепер можна визначити, чи є задана рівновага стабільною (стрілки, що вказують на точку) або нестабільною

Малюнок 3.1. Представницька поведінка рішення для\(y' = y - y^2\).

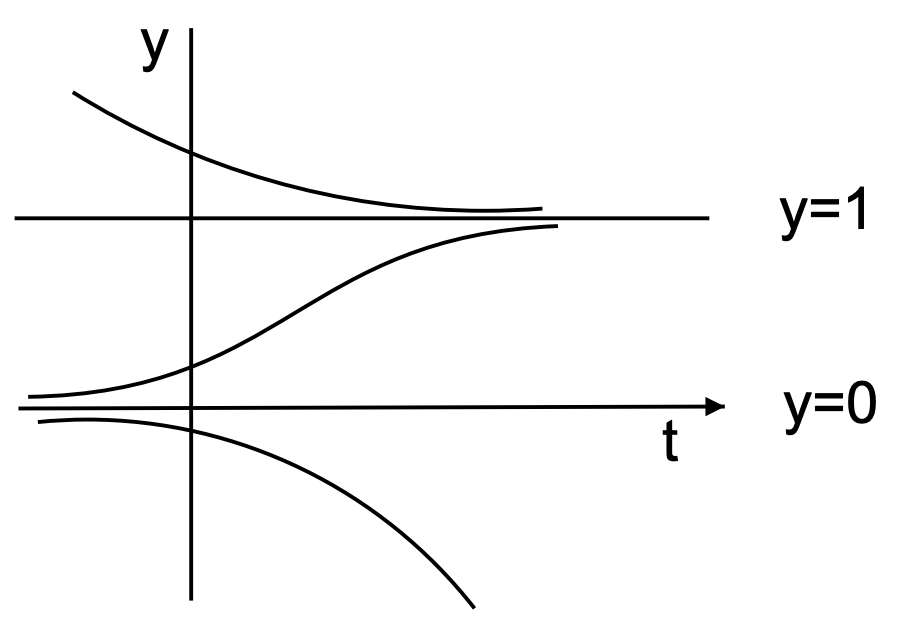
(Стрілки, що вказують в сторону від точки). На малюнку 3.3 проводимо кінцеву фазову лінію самостійно.

Малюнок 3.2. Представницька поведінка рішення та фазова лінія для\(y' = y - y^2\).