7.2: Зв'язані рівняння першого порядку

Розглянемо тепер загальну систему диференціальних рівнянь, за допомогою \[\label{eq:1}\overset{.}{x}_1=ax_1+bx_2,\quad\overset{.}{x}_2=cx_1+dx_2,\]якої можна записати за допомогою векторних позначень як \[\label{eq:2}\overset{.}{\mathbf{x}}=\mathbf{Ax}.\]

Перш ніж розв'язати цю систему од за допомогою матричних методів, я спочатку хочу показати, що ми могли б насправді вирішити ці рівняння шляхом перетворення системи в єдине рівняння другого порядку. Беремо похідну першого рівняння і використовуємо обидва рівняння для запису\[\begin{aligned}\overset{..}{x}_1&=a\overset{.}{x}_1+b\overset{.}{x}_2 \\ &=a\overset{.}{x}_1+b(cx_1+dx_2) \\ &=a\overset{.}{x}_1+bcx_1+d(\overset{.}{x}_1-ax_1) \\ &=(a+d)\overset{.}{x}_1-(ad-bc)x_1.\end{aligned}\]

Таким чином, система двох рівнянь першого порядку стає наступним рівнянням другого порядку:

\[\overset{..}{x}_1-(a+d)\overset{.}{x}_1+(ad-bc)x_1=0.\nonumber\]

Якби замість цього ми взяли похідну другого рівняння, ми б отримали однакове рівняння для\(x_2\):

\[\overset{..}{x}_2-(a+d)\overset{.}{x}_2+(ad-bc)x_2=0.\nonumber\]

Загалом система лінійних однорідних рівнянь\(n\) першого порядку може бути перетворена в еквівалентне лінійне однорідне рівняння\(n\) -го порядку. Чисельні методи зазвичай вимагають перетворення в зворотному напрямку; тобто перетворення рівняння\(n\) -го порядку в систему рівнянь\(n\) першого порядку.

З ансац\(x_1 = e^{\lambda t}\) або\(x_2 = e^{\lambda t}\) оди другого порядку мають характеристичне рівняння\[\lambda^2-(a+d)\lambda +(ad-bc)=0.\nonumber\]

Це ідентично характеристичному рівнянню, отриманому для матриці\(\mathbf{A}\) з аналізу власних значень.

Ми побачимо, що насправді\(\eqref{eq:1}\) можна вирішити, розглядаючи власні значення та власні вектори матриці\(\mathbf{A}\). Ми продемонструємо розв'язки для трьох окремих випадків: (i) власні значення\(\mathbf{A}\) дійсні і є два лінійно незалежних власних вектора; (ii) власні значення\(\mathbf{A}\) є складними сполученнями, і; (iii)\(\mathbf{A}\) має лише один лінійно незалежний власний вектор. Ці три випадки аналогічні випадкам, розглянутим раніше при розв'язанні однорідного лінійного рівняння постійного коефіцієнта другого порядку.

Різні реальні власні значення

Проілюструємо метод рішення на прикладі.

Приклад\(\PageIndex{1}\)

Знайдіть загальне рішення\(\overset{.}{x}_1=x_2+x_2,\:\overset{.}{x}_2=4x_1+x_2\).

Рішення

Переглянути підручник на YouTube

Розв'язуване рівняння може бути перезаписано в матричній формі як\[\frac{d}{dt}\left(\begin{array}{c}x_1\\x_2\end{array}\right)=\left(\begin{array}{cc}1&1\\4&1\end{array}\right)\left(\begin{array}{c}x_1\\x_2\end{array}\right),\nonumber\] або за допомогою векторних позначень, записаних як\(\eqref{eq:2}\). Ми приймаємо як наш ансац\(\mathbf{x}(t) = \mathbf{v}e^{\lambda t}\), де\(\mathbf{v}\) і\(\lambda\) є незалежними від\(t\). При підстановці на\(\eqref{eq:2}\), отримуємо\[\lambda\mathbf{v}e^{\lambda t}=\mathbf{Av}e^{\lambda t};\nonumber\] і при скасуванні експоненції отримуємо задачу на власні значення \[\label{eq:3}\mathbf{Av}=\lambda\mathbf{v}.\]

Знайшовши характеристичне рівняння за допомогою (7.1.8), ми маємо\[\begin{aligned}0&=\det (\mathbf{A}-\lambda\mathbf{I}) \\ &=\lambda^2-2\lambda -3 \\ &=(\lambda -3)(\lambda +1).\end{aligned}\]

Тому двома власними значеннями є\(\lambda_1=3\) і\(\lambda_2=-1\).

Для визначення відповідних власних векторів підставляємо власні значення послідовно в \[\label{eq:4}(\mathbf{A}-\lambda\mathbf{I})\mathbf{v}=0.\]

Ми запишемо відповідні власні вектори\(\mathbf{v_1}\) та\(\mathbf{v_2}\) використовуючи матричні позначення,\[\left(\begin{array}{cc}\mathbf{v_1}&\mathbf{v_2}\end{array}\right)=\left(\begin{array}{cc}v_{11}&v_{12} \\ v_{21}&v_{22}\end{array}\right),\nonumber\] де компоненти\(\mathbf{v_1}\) та\(\mathbf{v_2}\) записуються з індексами, відповідними першому та другому стовпцям\(2\times 2\) матриці.

Для\(\lambda_1 = 3\), і невідомий власний вектор\(\mathbf{v_1}\), ми маємо від\(\eqref{eq:4}\)\[\begin{aligned}-2v_{11}+v_{21}&=0, \\ 4v_{11}-2v_{21}&=0.\end{aligned}\]

Зрозуміло, що друге рівняння - це лише перше рівняння, помножене на\(−2\), тому лише одне рівняння є лінійно незалежним. Це завжди буде вірно, тому для\(2\times 2\) випадку нам потрібно розглянути тільки перший рядок матриці. Таким чином, перший власний вектор задовольняє\(v_{21} = 2v_{11}\). Нагадаємо, що власний вектор є унікальним лише до множення на константу: тому ми можемо взяти\(v_{11} = 1\) для зручності.

Для\(\lambda_2 = −1\), і власний вектор\(\mathbf{v_2} = (v_{12}, v_{22})^T\), ми маємо від\(\eqref{eq:4}\)\[2v_{12}+v_{22}=0,\nonumber\] так що\(v_{22}=-2v_{12}\). Ось, беремо\(v_{12}=1\).

Тому наші власні значення та власні вектори задаються\[\lambda_1=3,\:\mathbf{v_1}=\left(\begin{array}{c}1\\2\end{array}\right);\quad\lambda_2=-1,\:\mathbf{v_2}=\left(\begin{array}{c}1\\-2\end{array}\right).\nonumber\]

Вузол може бути привабливим або відштовхуючим залежно від того, чи є власні значення як негативними (як тут), так і позитивними. Зверніть увагу, що траєкторії руйнуються на\(\mathbf{v_2}\) власний вектор, так як\(\lambda_1 < \lambda_2 < 0\) і розпад відбувається швидше по\(\mathbf{v_1}\) напрямку.

Різні складні кон'югатні власні значення

Приклад\(\PageIndex{2}\)

Знайдіть загальне рішення\(\overset{.}{x}_1=-\frac{1}{2}x_1+x_2 ,\:\overset{.}{x}_2=-x_1-\frac{1}{2}x_2\).

Рішення

Переглянути підручник на YouTube

Рівняння в матричній формі\[\frac{d}{dt}\left(\begin{array}{c}x_1 \\ x_2\end{array}\right)=\left(\begin{array}{cc}-\frac{1}{2}&1 \\ -1&-\frac{1}{2}\end{array}\right)\left(\begin{array}{c}x_1 \\ x_2\end{array}\right).\nonumber\]

Ансац\(\mathbf{x} = \mathbf{v}e^{\lambda t}\) веде до рівняння\[\begin{aligned}0&=\det (\mathbf{A}-\lambda\mathbf{I}) \\ &=\lambda^2+\lambda +\frac{5}{4}.\end{aligned}\]

Тому\(\lambda = −1/2 ± i\); і ми спостерігаємо, що власні значення відбуваються як складна спряжена пара. Ми позначимо два власні значення як\[\lambda =-\frac{1}{2}+i\quad\text{and}\quad\overline{\lambda}=-\frac{1}{2}-i.\nonumber\]

Тепер, для\(\mathbf{A}\) реальної матриці, якщо\(\mathbf{Av} = \lambda\mathbf{v}\), то\(\mathbf{A}\mathbf{\overline{v}}=\overline{\lambda}\mathbf{\overline{v}}\). Тому власні вектори також зустрічаються у вигляді складної спряженої пари. Власний вектор,\(\mathbf{v}\) пов'язаний з власним значенням\(−iv_1 + v_2 = 0\),\(\lambda\) задовольняє, і нормалізуючи з\(v_1 = 1\), ми маємо\[\mathbf{v}=\left(\begin{array}{c}1 \\ i\end{array}\right).\nonumber\]

Тому ми визначили два незалежних комплексних розв'язку оди, тобто,\[\mathbf{v}e^{\lambda t}\quad\text{and}\quad\mathbf{\overline{v}}e^{\overline{\lambda}t},\nonumber\] і можемо сформувати лінійну комбінацію цих двох комплексних розв'язків для побудови двох незалежних реальних розв'язків. А саме, якщо складні функції\(z(t)\) і\(\overline{z}(t)\) записані як\[z(t)=\text{Re }\{z(t)\}+i\text{ Im }\{z(t)\},\quad\overline{z}(t)=\text{Re }\{z(t)\}-i\text{ Im }\{z(t)\},\nonumber\] то дві дійсні функції можуть бути побудовані з наступних лінійних комбінацій\(z\) і\(\overline{z}\):

\[\frac{z+\overline{z}}{2}=\text{Re }\{z(t)\}\quad\text{and}\quad\frac{z-\overline{z}}{2i}=\text{Im }\{z(t)\}.\nonumber\]

Таким чином, дві дійсні векторні функції, які можуть бути побудовані з двох наших складних векторних функцій:\[\begin{aligned}\text{Re }\{\mathbf{v}e^{\lambda t}\}&=\text{Re }\left\{\left(\begin{array}{c}1 \\ i\end{array}\right)e^{(-\frac{1}{2}+i)t}\right\} \\ &=e^{-\frac{1}{2}t}\text{Re }\left\{\left(\begin{array}{c}1\\i\end{array}\right)(\cos t+i\sin t)\right\} \\ &=e^{-\frac{1}{2}t}\left(\begin{array}{c}\cos t \\ -\sin t\end{array}\right);\end{aligned}\]

Малюнок\(\PageIndex{1}\): Фазовий портрет зі складними спряженими власними значеннями.

і\[\begin{aligned}\text{Im }\{\mathbf{v}e^{\lambda t}\}&=e^{-\frac{1}{2}t}\text{Im }\left\{\left(\begin{array}{c}1\\i\end{array}\right)(\cos t+i\sin t)\right\} \\ &=e^{-\frac{1}{2}t}\left(\begin{array}{c}\sin t\\ \cos t\end{array}\right).\end{aligned}\]

Прийняття лінійної суперпозиції цих двох реальних розв'язків дає загальний розв'язок оди, заданий\[\mathbf{x}=e^{-\frac{1}{2}t}\left(A\left(\begin{array}{c}\cos t \\-\sin t\end{array}\right)+B\left(\begin{array}{c}\sin t\\ \cos t\end{array}\right)\right).\nonumber\]

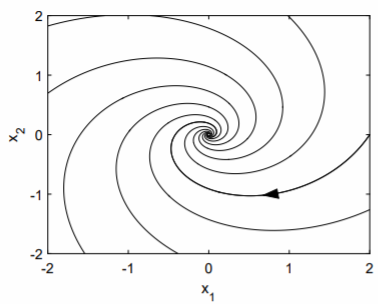
Відповідний фазовий портрет показаний на рис. \(\PageIndex{1}\). Ми говоримо, що походження - це спіральна точка. Якщо дійсна частина комплексу власногозначення від'ємна, як це відбувається тут, то розв'язки спіраль в початок. Якщо дійсна частина власногозначення позитивна, то розв'язки спіраль виходять з початку.

Напрямок спіралі - тут, це за годинниковою стрілкою - можна легко визначити. Якщо розглядати оду з\(x_1 = 0\) і\(x_2 = 1\), то побачимо, що\(\overset{.}{x}_1 = 1\) і\(\overset{.}{x}_2 = −1/2\). Траєкторія в точці\((0, 1)\) рухається вправо і вниз, і це можливо тільки в тому випадку, якщо спіраль знаходиться за годинниковою стрілкою. Траєкторія проти годинникової стрілки рухалася б вліво і вниз.

Повторювані власні значення з одним власним вектором

Приклад\(\PageIndex{3}\)

Знайдіть загальне рішення\(\overset{.}{x}_1=x_1-x_2,\:\overset{.}{x}_2=x_1+3x_2\).

Рішення

Переглянути підручник на YouTube

Рівняння в матричній формі \[\label{eq:5}\frac{d}{dt}\left(\begin{array}{c}x_1 \\ x_2\end{array}\right)=\left(\begin{array}{cc}1&-1 \\ 1&3\end{array}\right)\left(\begin{array}{c}x_1 \\ x_2\end{array}\right).\]

Ансац\(\mathbf{x} = \mathbf{v}e^{\lambda t}\) призводить до характеристичного рівняння\[\begin{aligned}0&=\det (\mathbf{A}-\lambda\mathbf{I}) \\ &=\lambda^2-4\lambda +4 \\ &=(\lambda -2)^2.\end{aligned}\]

Отже,\(\lambda = 2\) є повторюваним власним значенням. Асоційований власний вектор знаходиться з\(−v_1 − v_2 = 0\), або\(v_2 = −v_1\); і нормалізуючи з\(v_1 = 1\), ми маємо\[\lambda =2,\quad\mathbf{v}=\left(\begin{array}{c}1\\-1\end{array}\right).\nonumber\]

Таким чином, ми знайшли єдине рішення оди, надане\[\mathbf{x_1}(t)=c_1\left(\begin{array}{c}1\\-1\end{array}\right)e^{2t},\nonumber\] і нам потрібно знайти відсутнє друге рішення, щоб мати можливість задовольнити початкові умови. Ansatz\(t\) разів перше рішення спокусливо, але не вдасться. Тут ми обдуримо і знайдемо відсутнє друге рішення шляхом вирішення еквівалентного другого порядку, однорідного диференціального рівняння з постійним коефіцієнтом.

Ми вже знаємо, що це диференціальне рівняння другого порядку для\(x_1(t)\) має характеристичне рівняння з виродженим власним значенням, заданим\(\lambda = 2\). Тому загальне рішення для\(x_1\) дається\[x_1(t)=(c_1+tc_2)e^{2t}.\nonumber\]

Оскільки з першого диференціального рівняння\(x_2 = x_1 − \overset{.}{x}_1\), ми обчислюємо\[\overset{.}{x}_1=(2c_1+(1+2t)c_2)e^{2t},\nonumber\] так, що\[\begin{aligned}x_2&=x_1-\overset{.}{x}_1 \\ &=(c_1+tc_2)e^{2t}-(2c_1+(1+2t)c_2)e^{2t} \\ &=-c_1e^{2t}+c_2(-1-t)e^{2t}.\end{aligned}\]

Поєднуючи наші результати для\(x_1\) і\(x_2\), отже, ми знайшли\[\left(\begin{array}{c}x_1 \\ x_2\end{array}\right)=c_1\left(\begin{array}{c}1\\-1\end{array}\right)e^{2t}+c_2\left[\left(\begin{array}{c}0\\-1\end{array}\right)+\left(\begin{array}{c}1\\-1\end{array}\right)t\right]e^{2t}.\nonumber\]

Таким чином, наше відсутнє лінійно незалежне рішення визначено \[\label{eq:6}\mathbf{x}(t)=c_2\left[\left(\begin{array}{c}0\\-1\end{array}\right)+\left(\begin{array}{c}1\\-1\end{array}\right)t\right]e^{2t}.\]

Другий термін\(\eqref{eq:6}\) - це лише\(t\) раз перше рішення; однак цього недостатньо. Дійсно, правильний ансац, щоб знайти друге рішення безпосередньо, дається \[\label{eq:7}\mathbf{x}=(\mathbf{w}+t\mathbf{v})e^{\lambda t},\]

Малюнок\(\PageIndex{2}\): Фазовий портрет з одним власним вектором.

де\(\lambda\) і\(\mathbf{v}\) - власне значення та власний вектор першого розв'язку, і\(\mathbf{w}\) є невідомим вектором, який потрібно визначити. Щоб проілюструвати цей прямий метод, ми підставляємо\(\eqref{eq:7}\) в\(\mathbf{\overset{.}{x}} = \mathbf{Ax}\), припускаючи\(\mathbf{Av} = \lambda\mathbf{v}\). Скасувавши експоненціальну, отримуємо\[\mathbf{v}+\lambda (\mathbf{w}+t\mathbf{v})=\mathbf{Aw}+\lambda t\mathbf{v}.\nonumber\]

Подальше скасування загального терміну\(\lambda t\mathbf{v}\) і переписування прибутковості \[\label{eq:8}(\mathbf{A}-\lambda\mathbf{I})\mathbf{w}=\mathbf{v}.\]

Якщо\(\mathbf{A}\) має лише один лінійно незалежний власний вектор\(\mathbf{v}\), то\(\eqref{eq:8}\) можна вирішити для\(\mathbf{w}\) (інакше він не може). \(\mathbf{A}\)Використовуючи\(\lambda\) та наш\(\mathbf{v}\) нинішній приклад,\(\eqref{eq:8}\) система рівнянь, задана\[\left(\begin{array}{cc}-1&-1 \\ 1&1\end{array}\right)\left(\begin{array}{c}w_1\\w_2\end{array}\right)=\left(\begin{array}{c}1\\-1\end{array}\right).\nonumber\]

Перше і друге рівняння однакові, так що\(w_2 = −(w_1 + 1)\). Тому,\[\begin{aligned}\mathbf{w}&=\left(\begin{array}{c}w_1 \\ -(w_1+1)\end{array}\right) \\ &=w_1\left(\begin{array}{c}1\\-1\end{array}\right)+\left(\begin{array}{c}0\\-1\end{array}\right).\end{aligned}\]

Зверніть увагу, що перший член повторює перший знайдений розв'язок, тобто константа умножує власний вектор, а другий - новий. Тому ми приймаємо\(w_1 = 0\) і отримуємо\[\mathbf{w}=\left(\begin{array}{c}0\\-1\end{array}\right),\nonumber\], як раніше.

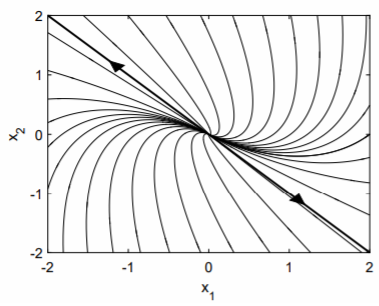
Фазовий портрет для цієї оди показаний на рис. \(\PageIndex{2}\). Темна лінія є єдиним\(\mathbf{v}\) власнимвектором матриці\(\mathbf{A}\). Коли існує тільки єдиний власнийвектор, походження називається неправильним вузлом.