6.1: Звичайні бали
- Page ID
- 61222
Якщо\(x_0\) є звичайною точкою (6.1), то можна визначити два силові ряди (тобто ряд Тейлора) розв'язки для\(y = y(x)\) центрованих на\(x = x_0\). Проілюструємо метод розв'язання двома прикладами, з\(x_0 = 0\).
Знайдіть загальне рішення\(y''+y=0\).
Рішення
Переглянути підручник на YouTube
На даний момент ви повинні знати, що загальним рішенням є\(y(x) = a_0 \cos x + a_1 \sin x\), з\(a_0\) і\(a_1\) константи. Щоб знайти рішення степеневого ряду про точку\(x_0 = 0\), пишемо\[y(x)=\sum\limits_{n=0}^{\infty}a_nx^n;\nonumber\] і після диференціації термін за терміном\[y'(x)=\sum\limits_{n=1}^{\infty}na_nx^{n-1},\nonumber\] і\[y''(x)=\sum\limits_{n=2}^{\infty}n(n-1)a_nx^{n-2}.\nonumber\]
Підставивши степеневий ряд for\(y\) та його похідні в розв'язуване диференціальне рівняння, отримаємо \[\label{eq:1}\sum\limits_{n=2}^{\infty}n(n-1)a_nx^{n-2}+\sum\limits_{n=0}^{\infty}a_nx^n=0.\]
Метод рішення серії потужності вимагає об'єднання двох сум на лівій стороні\(\eqref{eq:1}\) в один ряд потужності в\(x\). Щоб зсунути показник\(x^{n−2}\) в першій сумі вгору на два для отримання\(x^n\), нам потрібно зрушити індекс підсумовування вниз на два; тобто\[\sum\limits_{n=2}^{\infty}n(n-1)a_nx^{n-2}=\sum\limits_{n=0}^{\infty}(n+2)(n+1)a_{n+2}x^n.\nonumber\]
Потім ми можемо об'єднати дві суми\(\eqref{eq:1}\), щоб отримати \[\label{eq:2}\sum\limits_{n=0}^{\infty}\left((n+2)(n+1)a_{n+2}+a_n\right)x^n=0.\]
Для\(\eqref{eq:2}\) того, щоб бути задоволеним, коефіцієнт кожної потужності\(x\) повинен зникати окремо. (Це можна довести, встановивши\(x = 0\) після послідовної диференціації.) Таким чином, ми отримуємо рекуррентне відношення\[a_{n+2}=-\frac{a_n}{(n+2)(n+1)},\quad n=0,1,2,\ldots\nonumber\]
Ми спостерігаємо, що парні і непарні коефіцієнти розділяються. Таким чином, ми отримуємо дві незалежні послідовності, починаючи з першого члена\(a_0\) або\(a_1\). Розробляючи ці послідовності, ми маємо для послідовності, що починається з\(a_0\):
\[\begin{aligned}a_0&, \\ a_2&=-\frac{1}{2}a_0, \\ a_4&=-\frac{1}{4\cdot 3}a_2=\frac{1}{4\cdot 3\cdot 2}a_0, \\ a_6&=-\frac{1}{6\cdot 5}a_4=-\frac{1}{6!}a_0;\end{aligned}\]і загальний коефіцієнт в цій послідовності\(n = 0, 1, 2,\ldots\) для\[a_{2n}=\frac{(-1)^n}{(2n)!}a_0.\nonumber\]
Крім того, для послідовності, що починається з\(a_1\):
\[\begin{aligned}a_1&, \\ a_3&=-\frac{1}{3\cdot 2}a_1, \\ a_5&=-\frac{1}{5\cdot 4}a_3=\frac{1}{5\cdot 4\cdot 3\cdot 2}a_1, \\ a_7&=-\frac{1}{7\cdot 6}a_5=-\frac{1}{7!}a_1;\end{aligned}\]і загальний коефіцієнт в цій послідовності\(n = 0, 1, 2,\ldots\) для\[a_{2n+1}=\frac{(-1)^n}{(2n+1)!}a_1.\nonumber\]
Використовуючи принцип суперпозиції, загальне рішення є таким,\[\begin{aligned}y(x)&=a_0\sum\limits_{n=0}^\infty\frac{(-1)^n}{(2n)!}x^{2n}+a_1\sum\limits_{n=0}^\infty\frac{(-1)^n}{(2n+1)!}x^{2n+1} \\ &=a_0\left(1-\frac{x^2}{2!}+\frac{x^4}{4!}-\cdots\right)+a_1\left(x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots\right) \\ &=a_0\cos x+a_1\sin x,\end{aligned}\] як очікувалося.
У нашому наступному прикладі ми вирішимо рівняння Ейрі. Це диференціальне рівняння виникає при вивченні оптики, механіки рідини та квантової механіки.
Знайдіть загальне рішення\(y''-xy=0\).
Рішення
Переглянути підручник на YouTube
З\[y(x)=\sum\limits_{n=0}^\infty a_nx^n,\nonumber\] диференціальним рівнянням стає \[\label{eq:3}\sum\limits_{n=2}^\infty n(n-1)a_nx^{n-2}-\sum\limits_{n=0}^\infty a_nx^{n+1}=0.\]
Першу суму зрушуємо\(x^{n+1}\) на зміщення показника вгору на три, т. Е.\[\sum\limits_{n=2}^\infty n(n-1)a_nx^{n-2}=\sum\limits_{n=-1}^\infty (n+3)(n+2)a_{n+3}x^{n+1}.\nonumber\]
При об'єднанні двох сум в\(\eqref{eq:3}\), ми відокремлюємо додатковий\(n = −1\) член в першій сумі, заданій\(2a_2\). Тому\(\eqref{eq:3}\) стає \[\label{eq:4}2a_2+\sum\limits_{n=0}^\infty\left((n+3)(n+2)a_{n+3}-a_n\right)x^{n+1}=0.\]
Встановлюючи коефіцієнти ступенів від\(x\) до нуля, ми спочатку знайдемо\(a_2 = 0\), а потім отримуємо рекурсійне відношення \[\label{eq:5}a_{n+3}=\frac{1}{(n+3)(n+2)}a_n.\]
Три послідовності коефіцієнтів - ті, що починаються з\(a_0,\: a_1\) або\(a_2\) —decouple. Зокрема, три послідовності\[\begin{array}{l}a_0,a_3,a_6,a_9,\ldots ; \\ a_1,a_4,a_7,a_{10},\ldots ; \\ a_2,a_5,a_8,a_{11}\ldots\end{array}\nonumber\]
Так як\(a_2 = 0\), знаходимо відразу для останньої послідовності\[a_2=a_5=a_8=a_{11}=\cdots =0.\nonumber\]
Обчислено перші чотири ненульові члени в степеневому ряду з коефіцієнтами, відповідними першим двом послідовностям. Починаючи з\(a_0\) того, що ми маємо\[\begin{aligned}a_0&, \\ a_3&=\frac{1}{3\cdot 2}a_0, \\ a_6&=\frac{1}{6\cdot 5\cdot 3\cdot 2}a_0, \\ a_9&=\frac{1}{9\cdot 8\cdot 6\cdot 5\cdot 3\cdot 2}a_0;\end{aligned}\] і починаючи з того\(a_1\),\[\begin{aligned}a_1&, \\ a_4&=\frac{1}{4\cdot 3}a_1, \\ a_7&=\frac{1}{7\cdot 6\cdot 4\cdot 3}a_1, \\ a_{10}&=\frac{1}{10\cdot 9\cdot 7\cdot 6\cdot 4\cdot 3}a_1.\end{aligned}\]
Загальне рішення для\(y = y(x)\), отже, може бути записано як\[\begin{aligned}y(x)&=a_0\left(1+\frac{x^3}{6}+\frac{x^6}{180}+\frac{x^9}{12960}+\cdot\right) +a_1\left(x+\frac{x^4}{12}+\frac{x^7}{504}+\frac{x^{10}}{45360}+\cdot\right) \\ &=a_0y_0(x)+a_1y_1(x).\end{aligned}\]
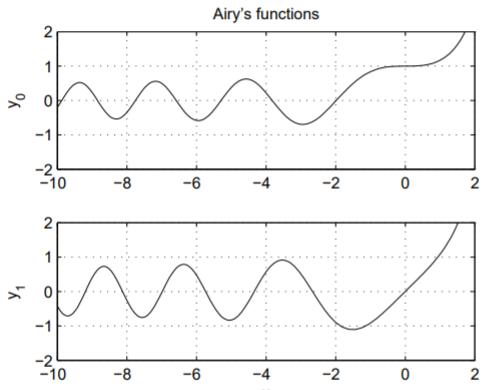
Припустимо, ми хотіли б зробити графік розв'язків\(y = y_0(x)\) і\(y = y_1(x)\) проти,\(x\) вирішуючи диференціальне рівняння\(y'' − xy = 0\) чисельно. Які початкові умови ми повинні використовувати? Зрозуміло,\(y = y_0(x)\) вирішує оду з початковими значеннями\(y(0) = 1\) і\(y' (0) = 0\), при цьому\(y = y_1(x)\) вирішує оду з початковими значеннями\(y(0) = 0\) і\(y' (0) = 1\).
Числові розв'язки, отримані за допомогою MATLAB, наведені на рис. \(\PageIndex{1}\). Зауважте, що розв'язки коливаються для негативних\(x\) і ростуть експоненціально для позитивних\(x\). Це можна зрозуміти, нагадавши, що\(y''+ y = 0\) має коливальний синус і косинус розв'язки і\(y'' − y = 0\) має експоненціальні гіперболічні синусоїди і косинуси розв'язки.