4.3: Теореми Чеви і Менелая

Last updated
Save as PDF

Page ID: 59046

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Чевіан (від$17^{\text {th }}$ століття італійського математика Джованні Чева (cheh'va)) - лінія трикутника від вершини до (невершинної) точки лінії протилежної сторони. Як приклади, медіани трикутника, його кутові бісектриси та його висоти - це все Севійці, але вони не повинні бути чимось таким особливим. Однак три з них разом призводять до дивовижного і потужного результату. Теорема була доведена Чевою, але вона також була доведена набагато раніше аль-Мутаман ібн Хюд, король Сарагоси, Іспанія одинадцятого століття.

Примітка

До цього моменту ми використовували лише позитивні заходи, але ця теорема також використовує негативні показники. Не має значення, який напрямок на лінії ми називаємо позитивним, але, як тільки це рішення буде прийнято, всі інші заходи на цій лінії узгоджуються, що і реверсування кінцевих точок відрізка лінії змінює свій знак.

Теорема (Теорема Чеви)

Севіани з кожної вершини є одночасними тоді і лише тоді, коли добуток підписаних співвідношень, які вони визначають на кожній бічній лінії, дорівнює 1. Тобто, на малюнку, Севіанці$\mathrm{AE}, \mathrm{BF}$, і$\mathrm{CD}$ є одночасними якщо і тільки тоді$(\mathrm{AD} / \mathrm{DB})(\mathrm{BE} / \mathrm{EC})(\mathrm{CF} / \mathrm{FA})=1$.

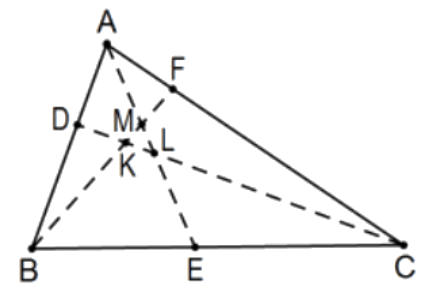
$Знімок екрана 2022-06-25 в 5.57.30 PM.png$

Доказ: Незалежно від того, чи є Севіани одночасними, розгляньте лінію на A, паралельну до лінії,$\mathrm{BC}$ і нехай$\mathrm{B}^{\prime}$ буде її перетин з лінією BF та$\mathrm{C}^{\prime}$ її перетином із CD. Навіть без загального перетину Севіан, конгруентні альтернативні внутрішні кути та вертикальні кути перевіряють п'ять пар подібних трикутників;$\mathrm{D}$ і$\mathrm{F}$ мають на увазі, що$\triangle \mathrm{AC}{ }^{\prime} \mathrm{D} \sim \triangle \mathrm{BCD}$$\triangle \mathrm{AB}^{\prime} \mathrm{F} \sim \triangle \mathrm{CBF}$ і три з перетинами кожного пара Севіан, AE з BF, AE з CD, і BF з CD. Довільно, ми приймаємо напрямки на кожному рядку як позитивні, якщо вершина до вершини або вершина до Севіана алфавітно збільшується і в$A$ напрямку$B^{\prime}$ вздовж решти.

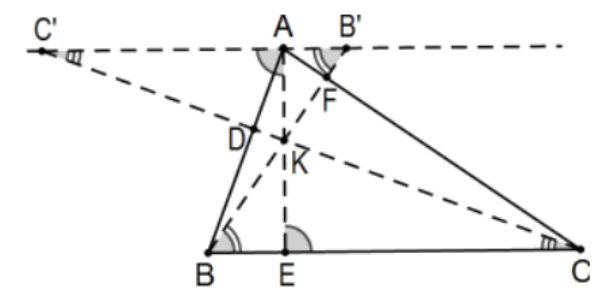
$Знімок екрана 2022-06-25 в 5.58.56 PM.png$

Вони призводять до багатьох пар однакових співвідношень, включаючи:

$\left(\mathrm{AD} / \mathrm{BD}=-\mathrm{AC}^{\prime} /-\mathrm{BC}\right) \Rightarrow(\mathrm{AD} / \mathrm{DB}=\mathrm{AC} / \mathrm{CB})$(турбуючись про підписані заходи) і
$\mathrm{CF} / \mathrm{FA}=\mathrm{CB} / \mathrm{B}^{\prime} \mathrm{A}$(Ознаки заходів вже згодні). Припустимо, ці три Севіанці перетинаються в одній точці, скажімо$K$. Потім$\triangle \mathrm{AB}{ }^{\prime} \mathrm{K} \sim \triangle \mathrm{EBK}$ і$\Delta \mathrm{AC}^{\prime} \mathrm{K} \sim \Delta \mathrm{ECK}$ так, що:$\left(\mathrm{AB}^{\prime} / \mathrm{EB}=\mathrm{AK} / \mathrm{EK}=-\mathrm{AC}^{\prime} /-\mathrm{EC}\right) \Rightarrow\left(\mathrm{EB} / \mathrm{AB}^{\prime}=\mathrm{EC} / \mathrm{AC}{ }^{\prime}\right)$ (взаємно першого і останнього) і
$\left(\mathrm{EB} / \mathrm{EC}=\mathrm{AB}^{\prime} / \mathrm{AC}^{\prime}\right) \Rightarrow\left(\mathrm{BE} / \mathrm{EC}=\mathrm{B}^{\prime} \mathrm{A} / \mathrm{AC}\right.$') (Знаки знову, а також «взаємозамінні засоби»). Множимо рівняння$(1),(3)$$(2)$, і, відповідно, маємо:

\[(\mathrm{AD} / \mathrm{DB})(\mathrm{BE} / \mathrm{EC})(\mathrm{CF} / \mathrm{FA})=(\mathrm{AC} / \mathrm{CB})\left(\mathrm{B}^{\prime} \mathrm{A} / \mathrm{AC}^{\prime}\right)\left(\mathrm{CB} / \mathrm{B}^{\prime} \mathrm{A}\right)=1 \nonumber\]

Зворотним є те, що, якщо рівняння тримає, то$\mathrm{AE}, \mathrm{BF}, \mathrm{CD}$ є одночасними. Щоб довести це, припустимо, що$\mathrm{K}$ це точка перетину тільки двох Севіан,$B F$ і$C D$, нехай$E^{\prime}$ буде перетин лінії АК з лінією$\mathrm{BC}$. Потім, з частини теореми тільки що доведено, (AD/DB)$\left(\mathrm{BE}^{\prime} / \mathrm{E}^{\prime} \mathrm{C}\right)(\mathrm{CF} / \mathrm{FA})=1$ і, за гіпотезою, ми маємо це (AD/DB) (BE/EC)$(\mathrm{CF} / \mathrm{FA})=1$. Проста алгебра дає$\mathrm{BE}^{\prime} / \mathrm{E}^{\prime \prime} \mathrm{C}=\mathrm{BE} / \mathrm{EC}$ і, додаючи по 1 в кожну сторону і додаючи отримані змішані дроби, ми маємо$\left(\mathrm{BE}^{\prime}+\mathrm{E}^{\prime} \mathrm{C}\right) / \mathrm{E}^{\prime} \mathrm{C}=(\mathrm{BE}+\mathrm{EC}) / \mathrm{EC}$. Помітивши, що$\mathrm{E}^{\prime}$ знаходиться між$\mathrm{B}$$\mathrm{C}$ і так є$\mathrm{E}$, чисельники обидва спрощують до BC. Тобто,$\mathrm{BC} / \mathrm{E}^{\prime} \mathrm{C}=\mathrm{BC} / \mathrm{EC}$. З цього відразу випливає, що$\mathrm{E}^{\prime} \mathrm{C}=\mathrm{EC}$ і, з їхньої коллінеарності та Постулату Правителя, E' = E, що доводить, що Севіани є одночасними. КАД.

Чи потрібна «підписана» деталь? Чи можна мати добуток цих співвідношень$-1$? Мало того, що відповідь «так», результат - важлива теорема сама по собі. Є деякі приємні наслідки теореми Чеви. Пару з них ми вже бачили, але є майже тривіальними наслідками цієї теореми. Воістину тривіальним є те, що медіани трикутника є одночасними. PS 4, #26 є нетривіальним доказом, але також дає більше інформації.

Трохи більше залучено ще один доказ того, що кутові бісектриси трикутника є одночасними. Цього разу теорема пропорційності для кутових бісектрис дає відповідь (див. PS 4, #33). Більш складна, але показова сила теореми:

Теорема

Висоти трикутника одночасні (точка перетину називається ортоцентром).

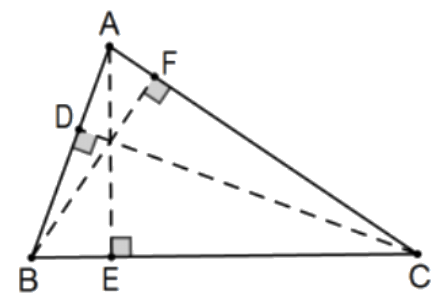
$Знімок екрана 2022-06-25 в 6.00.55 PM.png$

Доказ: Розглянемо гострі$\triangle \mathrm{ABC}$ і нехай E, F і D будуть футами висот від вершин A, B і C відповідно. За АА подібність:$\triangle \mathrm{CAD} \sim \triangle \mathrm{BAF}$ ($\angle \mathrm{A}$в загальному)$\triangle \mathrm{ABE} \sim \triangle \mathrm{CBD}$ ($\angle \mathrm{B}$в загальному)$\triangle \mathrm{BCF} \sim \triangle \mathrm{ACE}(\angle \mathrm{C}$ в загальному)

$Знімок екрана 2022-06-25 в 6.03.40 PM.png$

Як і раніше, присвоюючи позитивний знак від$A$$B, B$ до$C$, і$A$ до$C$:

$[\mathrm{AD} / \mathrm{CA}=\mathrm{AF} / \mathrm{BA}] \Rightarrow[(\mathrm{AD} / \mathrm{CA})(\mathrm{BA} / \mathrm{AF})=1]$

$[\mathrm{BE} / \mathrm{AB}=-\mathrm{BD} /-\mathrm{CB}] \Rightarrow[(\mathrm{BE} / \mathrm{AB})(\mathrm{CB} / \mathrm{BD})=1]$

$[\mathrm{CF} / \mathrm{BC}=-\mathrm{CE} /-\mathrm{AC}] \Rightarrow[(\mathrm{CF} / \mathrm{BC})(\mathrm{AC} / \mathrm{CE})=1]$

Множення цих трьох дає рівняння:

\ [\ begin {вирівнювання*} 1 &= [(\ mathrm {AD}/\ математика {CA}) (\ математика {BA}/\ математика {AF})] [(\ mathrm {AB}) (\ математика {CB}/\ математика {BD})] [\ mathrm {CF}/математика {BC}) (\ математика {AC}/\ mathrm {CE})]\\ [4pt]
&= [(\ математика {AD}\ cdot\ mathrm {BE}\ cdot\ mathrm {CF}) (\ mathrm {BA}\ cdot\ mathrm {CB} \ cdot\ математика {AC})/[(\ mathrm {BD}\ cdot\ mathrm {CE}\ cdot\ mathrm {AF}) (\ mathrm {CA}\ cdot\ mathrm {BC})]\\ [4pt]
&= [(\ mathrm {AD}\ cdot\ mathrm\ cdot\ mathrm Therm {BE}\ cdot\ mathrm {CF}) (\ mathrm {BA}\ cdot\ mathrm {CB}\ cdot\ mathrm {AC})/[(\ mathrm {DB}\ cdot\ mathrm {AC} \ cdot\ mathrm {BA}\ cdot\ mathrm {CB})]\\ [4pt]
&= [(\ математика {AD}/\ mathrm {DB}) (\ mathrm {CE}) (\ mathrm {CF}/\ mathrm {FA})] [\ mathrm {BA}/математика {BA}) (\ математика {CB}/\ математика {CB}) (\ математика {AC}/\ математика {AC})]\\ [4pt]
& =(\ mathrm {AD}/\ mathrm {DB}) (\ mathrm {BE}/\ mathrm { EC}) (\ mathrm {CF}/\ mathrm {FA})\ end {вирівнювання*}\]

За теоремою Чеви, рядки AE, BF та CD є одночасними.

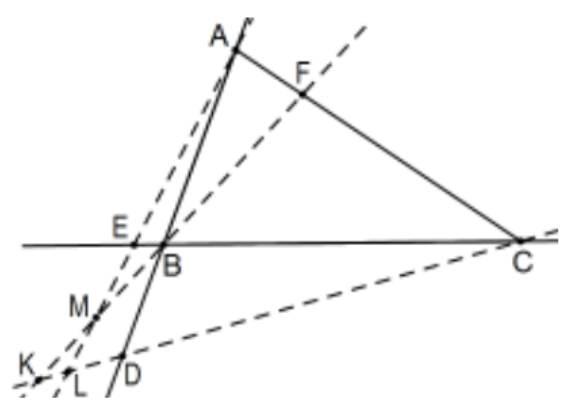
$Знімок екрана 2022-06-25 о 6.08.44 PM.png$

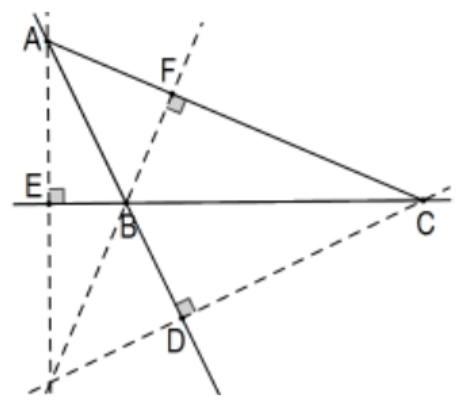
Однак, як випливає з другої цифри, нам потрібно розширити результат до тупих трикутників. Озираючись назад на подібні трикутники, що використовуються в гострому випадку, зазначені трикутники все ще схожі, але є поворот, той, який використовує загальні$\angle$ B, використовує вертикальні кути замість загального кута. При цьому самі коефіцієнти, як і раніше, тримаються і, перевіряючи, так роблять і знаки коефіцієнтів. Через цей факт, той самий доказ конгруентності висот все ще працює за умови Теорема Чеви також має для тупих трикутників. На щастя, це так. Якщо дві точки Чевіана знаходяться поза відповідними сторонами трикутника, Теорема Чеви все ще тримає:

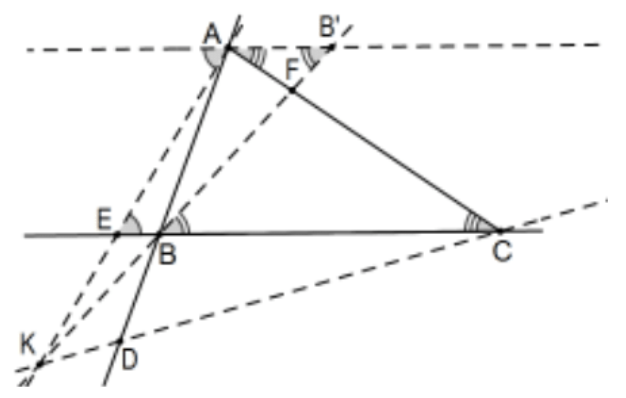
$Знімок екрана 2022-06-25 на 6.09.55 PM.png$

На малюнку D знаходиться поза сегментом$\mathrm{AB}$ і$\mathrm{E}$ знаходиться поза сегментом BC. Припускаючи призначення напрямків, як і раніше, на цей раз$\mathrm{DB}$ і$\mathrm{BE}$ є негативними, поки$\mathrm{F}$ все ще між ними$\mathrm{A}$ і$\mathrm{C}$$\mathrm{CF}$ так має один і той же знак. Тоді, перетинаються лінії в одній точці чи ні,$(AD/DB)(BE/EC)(CF/FA)$ є позитивним. Цей факт може трохи спростити механіку доказу тим, що ми могли б ігнорувати їх ознаки і вважати всі довжини позитивними, спостереження, яке означало б, що нам не довелося б турбуватися про два розвороти одночасно у внутрішньому випадку. Продовжуючи точно так, як і раніше, розгляньте паралель на A протилежній бічній лінії$B C$ з$B^{\prime}$ і$C^{\prime}$ ($C^{\prime}$знаходиться поза сторінкою праворуч) як раніше і позитивний напрямок від$A$ до $B^{\prime}$так що, на цей раз,$A C^{\prime}$ є позитивним. Всі виявлені трикутники все ще схожі (загальна вершина на D і$\mathrm{K}$ замість вертикальних кутів) так, що$\triangle \mathrm{AC}{ }^{\prime} \mathrm{D} \sim \triangle \mathrm{BCD}$$\triangle \mathrm{AB}{ }^{\prime} \mathrm{F} \sim \triangle \mathrm{CBF}$ і тому:

$\left(\mathrm{AD} / \mathrm{BD}=\mathrm{AC}^{\prime} / \mathrm{BC}\right) \Rightarrow(\mathrm{AD} / \mathrm{DB}=\mathrm{AC} / \mathrm{CB})$(турбуючись про підписані заходи) і
$\left(\mathrm{AF} / \mathrm{CF}=\mathrm{AB}^{\prime} / \mathrm{CB}\right) \Rightarrow\left(\mathrm{CF} / \mathrm{FA}=\mathrm{CB} / \mathrm{B}^{\prime} \mathrm{A}\right.$) (прийняття взаємних і зворотних двох підписаних заходів). Припустимо, ці три Севіанці перетинаються в одній точці, скажімо$K$. Потім$\triangle A B^{\prime} K \sim \Delta E B K$ і$\Delta \mathrm{AC}{ }^{\prime} \mathrm{K} \sim \Delta \mathrm{ECK}$ так, щоб$\left(\mathrm{AB}^{\prime} / \mathrm{EB}=\mathrm{AK} / \mathrm{EK}=\mathrm{AC}^{\prime} / \mathrm{EC}\right) \Rightarrow\left(\mathrm{EB} / \mathrm{AB}^{\prime}=\mathrm{EC} / \mathrm{AC}^{\prime}\right)$ і
$\left(\mathrm{EB} / \mathrm{EC}=\mathrm{AB}^{\prime} / \mathrm{AC}^{\prime}\right) \Rightarrow\left(\mathrm{BE} / \mathrm{EC}=\mathrm{B}^{\prime} \mathrm{A} / \mathrm{AC}{ }^{\prime}\right)$(«взаємозамінні засоби» і знаки знову). Це точно такі ж три рівняння, які ми мали раніше, так що, якщо Севіанці дійсно перетинаються, то добуток співвідношень дорівнює 1. І навпаки, якщо ми припустимо, що$K$ це точка перетину двох Cevians BF$\mathrm{CD}$ і нехай$\mathrm{E}^{\prime}$ буде перетин лінії$\mathrm{AK}$ з лінією$\mathrm{BC}$, ми можемо діяти точно так, як раніше. КВЕД

Оскільки теорема Чеви відносно нова, дещо дивно з'ясувати, що випадок$-1$ датується давниною з її відкриттям та першим доказом невідомим. Теорема називається теоремою Менелая, але Менелай був фігурою з грецької міфології, а не одним з великих грецьких геометрів. Як і у випадку з теоремою Чеви, є багато доказів цієї знаменитої теореми.

Теорема (Теорема Менелая)

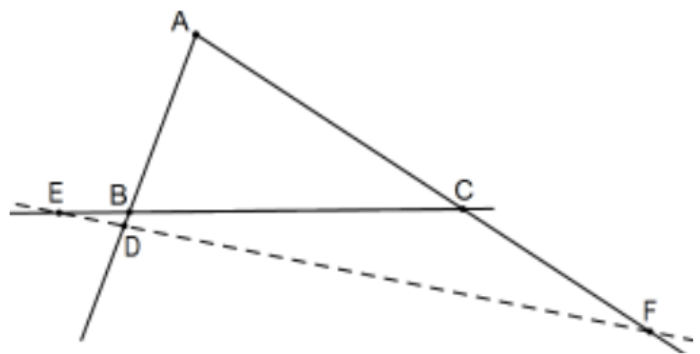
Три точки, одна невершинна точка з кожної бічної лінії трикутника, є колінеарними тоді і лише тоді, коли добуток підписаних співвідношень, які вони визначають на всіх трьох бічних лініях$-1$. Тобто, на малюнку$\mathrm{D}, \mathrm{E}$, і$\mathrm{F}$ колінеарні якщо і тільки тоді$(\mathrm{AD} / \mathrm{DB})(\mathrm{BE} / \mathrm{EC})(\mathrm{CF} / \mathrm{FA})=-1$.

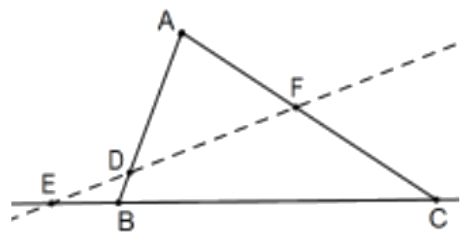
$Знімок екрана 2022-06-25 в 6.16.29 PM.png$

Доказ: Якщо ви ще не помітили, ці співвідношення є позитивними тоді і лише тоді, коли точка знаходиться всередині його сторони (чисельник та знаменник позитивні або негативні разом). Причому, якщо один з них знаходиться на самому трикутнику, два повинні бути. Тобто, якщо три точки є колінеарними, лінія, яку вони визначають, перетинає внутрішню частину сторін трикутника або в двох, або без точок, і обидві вони можливі, як вказують цифри.

Тобто, якщо точки колінеарні, або одне співвідношення є негативним, або всі три негативні, і, в будь-якому випадку, добуток коефіцієнтів негативний, тому нам насправді не потрібно турбуватися про підписані заходи; продукт буде негативним.

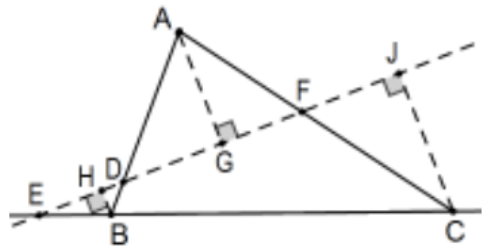
$Знімок екрана 2022-06-25 в 6.19.02 PM.png$ $Знімок екрана 2022-06-25 в 6.19.39 PM.png$

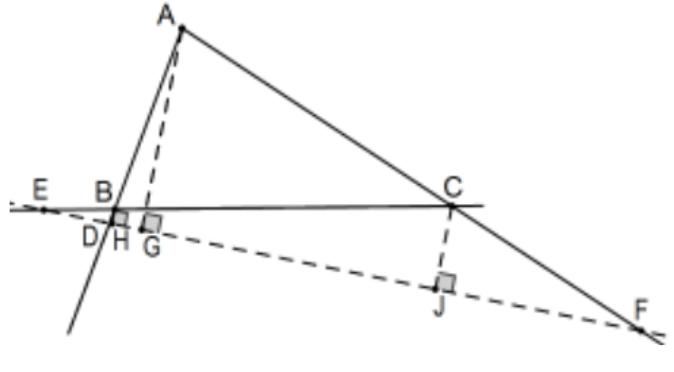
Щоб почати доказ випадку двох перетинів, припустимо$\mathrm{D}, \mathrm{E}$, і$F$ є колінеарними і відкидають перпендикуляр від кожної вершини. AA Подібність дає кілька подібних трикутників (E) у загальних та вертикальних кутах$\mathrm{D}$$\mathrm{F}$ у двосторонньому випадку та, у випадку з нульовою стороною, загальні кути під$\mathrm{E}$$\mathrm{F}$ та вертикальними кутами при$\mathrm{D})$:

$[(\mathrm{AD} / \mathrm{AG}=\mathrm{BD} / \mathrm{BH})] \Rightarrow[(\mathrm{AD} / \mathrm{BD}=\mathrm{AG} / \mathrm{BH})]$(Обмінні засоби)$[(\mathrm{BE} / \mathrm{BH}=\mathrm{CE} / \mathrm{CJ})] \Rightarrow[(\mathrm{BE} / \mathrm{CE}=\mathrm{BH} / \mathrm{CJ})]$ (засоби обміну)$[(\mathrm{CF} / \mathrm{CJ}=\mathrm{AF} / \mathrm{AG})] \Rightarrow[(\mathrm{CF} / \mathrm{AF}=\mathrm{CJ} / \mathrm{AG})]$ (засоби обміну) З цих трьох ми маємо:

$(\mathrm{AD} / \mathrm{DB})(\mathrm{BE} / \mathrm{EC})(\mathrm{CF} / \mathrm{FA})=(\mathrm{AG} / \mathrm{HB})(\mathrm{BH} / \mathrm{JC})(\mathrm{CJ} / \mathrm{GA})$$=(\mathrm{AG} / \mathrm{GA})(\mathrm{BH} / \mathrm{HB})(\mathrm{CJ} / \mathrm{JC})=(-1)^{3}=-1$

і теорема Менелая доведена в одному напрямку.

$Знімок екрана 2022-06-25 в 6.20.19 PM.png$

Доказ зворотного випливає з цього результату так само, як і з Ceva. Тобто припустимо, що цей твір є$-1$ і нехай$\mathrm{E}^{\prime}$ буде перетин лінії DF з лінією BC. За щойно доведеною теоремою ми маємо:

\[(\mathrm{AD} / \mathrm{DB})(\mathrm{BE} / \mathrm{EC})(\mathrm{CF} / \mathrm{FA})=(\mathrm{AD} / \mathrm{DB})\left(\mathrm{BE}^{\prime} / \mathrm{E}^{\prime} \mathrm{C}\right)(\mathrm{CF} / \mathrm{FA}) \nonumber\]

і те, що$\mathrm{E}=\mathrm{E}^{\prime}$ випливає точно так, як і раніше. КАД.