4.1: Евклідова геометрія
- Page ID
- 59055
Всі інші аксіоми та визначення (які залишаються невизначеними!) нейтральної геометрії залишаються в силі, але додатково додаємо:
Існує лінія і точка не на цій лінії, так що на цій точці є не більше однієї лінії, яка паралельна вихідній лінії.
[Примітка: Згадайте з нейтральної геометрії, що у нас завжди є принаймні одна паралель, так що тепер точно одна паралель.]
Для будь-якої лінії та будь-якої точки, яка не знаходиться на цій лінії, є не більше однієї лінії на цій точці, яка паралельна вихідній лінії.
Ці дві аксіоми рівнозначні.
Доказ: Очевидно, глобальний має на увазі локальний. І навпаки, припустимо, що Local вірно. Тоді, оскільки випадок «без паралелей» не існує (ми перебуваємо в нейтральній геометрії), заперечення Global означало б деяку лінію, а якусь точку не на тій лінії, в якій було кілька паралелей. Але тоді глобальна форма Гіперболічного паралельного постулату означала б, що дана локальна гіперболічна ситуація повинна бути правдою, необхідним протиріччям. КАД.
Сума кутів трикутника дорівнює двом прямим кутам. [Так для\(n\) -кутника, точно\(180(n-2)\).]
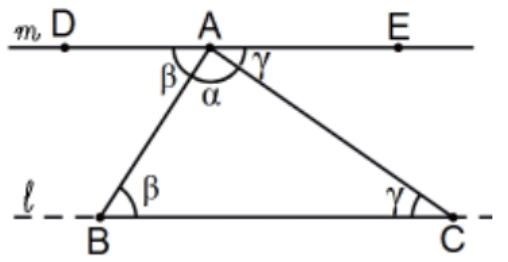
Доказ: Розглянемо будь-який трикутник, скажімо\(\triangle \mathrm{ABC}\). На А на АВ, а на протилежному боці скопіюйте\(\angle A B C\), скажімо\(\angle D A B\), і при А на змінному, а на протилежному боці,\(\angle A C B\) копію для отримання\(\angle \mathrm{EAC}\). Чому лінія\(\mathrm{DA}=\mathrm{AE}\) така\(\alpha+\beta+\gamma=180^{\circ}\)?
Якщо дві паралельні лінії розрізаються поперечним, вони утворюють конгруентні альтернативні внутрішні кути з поперечними [і чергують зовнішні кути та відповідні кути].
Доказ: PS 4, #2. Примітка: Це дає ще один легкий доказ теореми про кутову суму - почніть з паралелі.
Площа квадрата довжини 1 одиниці дорівнює 1 квадратній одиниці і, за розширенням, площа будь-якого\(m \times n\) прямокутника дорівнює mn квадратних одиниць. Площа скінченної, обмеженої, простої (без перекриттів), області (в площині) - найбільша нижня межа сум площ всіх прямокутників, які можуть бути вписані всередину області без перекриття їх інтер'єрів за умови, що число дорівнює найменшій верхній межі сум площ всіх прямокутники, які містять область без перекриття їх інтер'єрів.
[Примітка: Щоб довести, що це визначення є значущим, потрібен більш реальний аналіз, ніж ми збираємося припустити.]
Два трикутника еквівалентні тоді і тільки тоді, коли вони мають однакову площу. Більш загально, трикутник еквівалентний\(n\) -gon, якщо вони мають однакову площу.
Доказ: Не повинно дивуватися, що площа буде збережена при еквівалентності, але чому б не в гіперболічній геометрії? Тим не менш, одним доказом (лише для трикутників) є зміна відповідної теореми в гіперболічній геометрії шляхом заміни кожного входження «суми кута» на «площа» (PS 4, #28). Чи існують менш складні докази? Абсолютно. Для інших багатокутників введіть кількість сторін (PS 4, #33). (Це не вірно для суми кута в гіперболічній геометрії.) КАД.
Формули площі звичайних багатокутників.
Якщо\(\triangle \mathrm{ABC}\) зі сторонами\(\mathrm{a}, \mathrm{b}, \mathrm{c}\) - прямокутний трикутник з прямим кутом в\(\mathrm{C}\), то\(\mathrm{a}^{2}+\mathrm{b}^{2}=\mathrm{c}^{2}\). Тобто сума площ квадратів на двох його катетках дорівнює площі квадрата на його гіпотенузі.
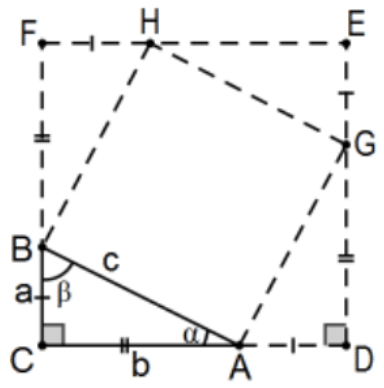
Доказ 1: Є багато доказів цього результату; деякі зовсім відрізняються від інших. Серед найпростіших - побудувати квадрат сторін\(a+b\) навколо трикутника і використовувати трохи алгебри. Додавання областей частин, які ми маємо\((\mathrm{a}+\mathrm{b})^{2}=4((1 / 2) \mathrm{ab})+\mathrm{c}^{2}\), що спрощує:\(\mathrm{a}^{2}+\mathrm{b}^{2}=\mathrm{c}^{2}\). Деталі залишені як\(\mathrm{PS} 4\), #19. КАД.
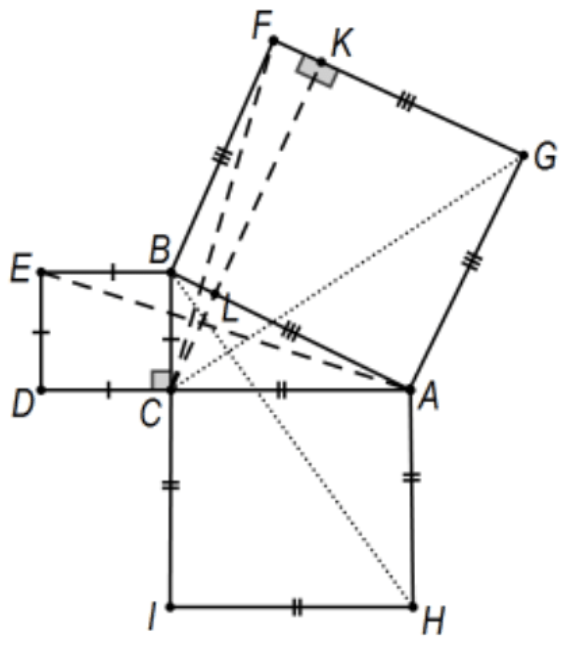
Доказ 2: Це традиційний доказ з елементів Евкліда в книзі 1, Prop 47, і кожен майбутній вчитель геометрії середньої школи повинен бути знайомий з ним. З трохи більше роботи, він може бути скоригований, щоб довести квадрати еквівалентні; тобто, два менші квадрати можуть бути «розрізані» на кінцеву кількість частин і переставити в більшу. У прямокутному трикутнику фігури\(\triangle \mathrm{ABC}\), з квадратами з кожного боку, припускають допоміжні лінії, як вони з'являються при КК, визначеної лінією на\(C\) перпендикулярній гіпотенузі\(A B\) вихідного прямокутного трикутника. Площа\(\triangle \mathrm{EBA}\) становить половину площі малого квадрата BCDE (база BE та висота\(\mathrm{BC}\)) і, по SAS,\(\triangle \mathrm{EBA} \cong \triangle \mathrm{CBF}\) (повернути\(90^{\circ}\) приблизно на точку\(\mathrm{B}\)). Для другого трикутника використовуйте основу БФ висотою BL. Таким чином, квадрат BCDE має таку ж площу, як і прямокутник BFKL. За симетрією (відрізки BH і\(\mathrm{CG}\)) квадрат\(\mathrm{ACIH}\) і прямокутник\(\mathrm{AGKL}\) мають однакову площу. КАД.
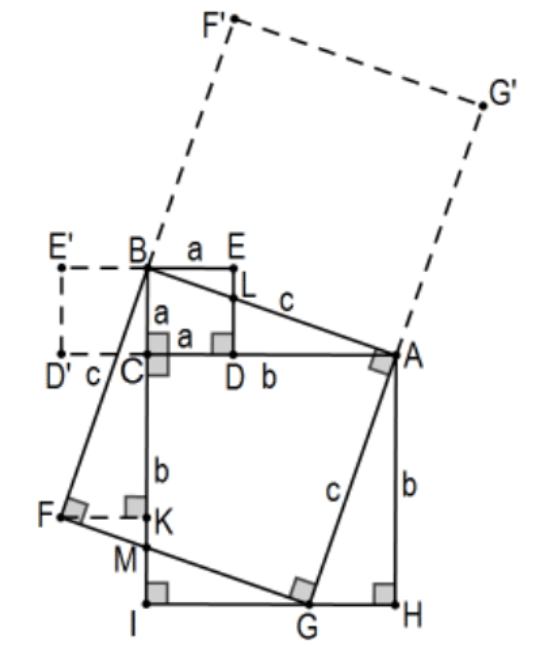
Доказ 3: Набагато простіше є доказом, який безпосередньо доводить, що два менші квадрати еквівалентні більшому. У цьому складіть квадрат на одному катеті, щоб перекрити трикутник, і складіть квадрат на гіпотенузі як через трикутник, так і сусідні квадрати. Зауважте\(\mathrm{D}^{\prime}, \mathrm{E}^{\prime}, \mathrm{F}^{\prime}\), що, і не\(\mathrm{G}^{\prime}\) є частиною доказу; вони є лише для того, щоб допомогти візуалізувати ситуацію в її традиційному вигляді. Дивно, але для цього потрібна тільки одна допоміжна лінія\(\mathrm{FK}\), де\(\mathrm{K}\) перпендикуляр\(\mathrm{F}\) на лінії\(\mathrm{BC}\). Ідея полягає в тому, щоб показати, що квадрат на\(\mathrm{BC}\left(\mathrm{a}^{2}\right)\) разом з\(\mathrm{AC}\left(\mathrm{b}^{2}\right)\) квадратом на еквівалентний квадрату на\(\mathrm{AB}\left(\mathrm{c}^{2}\right)\). Оскільки існує так багато перекриття, еквівалентність вимагає лише підтвердження того\(\triangle \mathrm{AGH} \cong \triangle \mathrm{BFK}\)\(\triangle \mathrm{BLE} \cong \triangle \mathrm{FMK}\),\(\triangle \mathrm{ALD} \cong \triangle \mathrm{GMI}\) і що\(\mathrm{G}\) колінеарно з\(\mathrm{H}\) і I. Деталі залишаються як PS 4, #20. КАД.
Інші докази наведені в PS 4, #21 -24.
Якщо\(\triangle \mathrm{ABC}\) такий що\(\mathrm{a}^{2}+\mathrm{b}^{2}=\mathrm{c}^{2}\), то це прямокутний трикутник з прямим кутом під\(\mathrm{C}\).
Доказ: Побудувати прямокутний трикутник з ніжками розміру a і b За теоремою Піфагора третя сторона...? Тоді по ССС...? КАД.
Відрізок, що з'єднує середні точки двох сторін трикутника, становить половину довжини третьої сторони і паралельно їй.
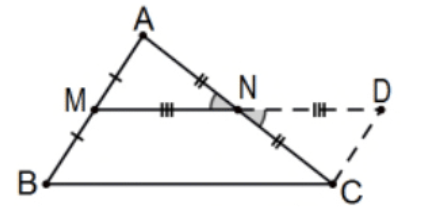
Доказ: Дозвольте\(\mathrm{M}\) і\(\mathrm{N}\) бути серединами сегментів\(\mathrm{AB}\) і\(\mathrm{AC}\) з\(\triangle \mathrm{ABC}\) і подвійний сегмент,\(\mathrm{MN}\) щоб визначити\(\mathrm{D}\), як зазначено. З вертикальними кутами у\(\mathrm{N}\) нас є\(\triangle \mathrm{CND} \cong \triangle \mathrm{ANM}\) SAS. Потім\(\mathrm{AM} \cong \mathrm{CD}\) і\(\angle \mathrm{DCN} \cong \angle \mathrm{A}\) по cpctc і у нас є конгруентні альтернативні внутрішні кути так лінії\(\mathrm{AM}=\mathrm{BM}\) і\(\mathrm{CD}\) паралельні. З\(\mathrm{AM} \cong \mathrm{BM}\) таким чином\(\mathrm{BM} \cong \mathrm{CD}\), у нас є чотирикутник BCDM з парою протилежних сторін, які є паралельними і конгруентними. Оскільки ми знаходимося в евклідовій геометрії, чотирикутник є паралелограмом (PS 4, #15), тому його протилежні сторони є конгруентними (PS 4, #12). Тобто MD\(\cong B C\) і, оскільки\(\mathrm{MN} \cong \mathrm{ND}\) за конструкцією,\(\mathrm{N}\) є середньою точкою сегмента MD, як відомо, є конгруентною до нашої ери. Таким чином, ми маємо відрізок MN паралельно і половині сегмента BC за потребою. КАД.
Два багатокутника схожі (вказується ««), а відповідність подібність, якщо (так якщо) існує пропорційна відповідність між їх сторонами, що зберігає його кути; тобто 1-1 відповідність сторін однієї з іншою з додатним дійсним числом r, загальне співвідношення, таке, що довжина другого - довжина першої помножена на\(\mathrm{r}\) і кут між двома відповідними сторонами незмінний.
Наприклад,\(\triangle\) MAN\(\sim \triangle B A C\) з\(r=2\) в останній теоремі, оскільки інші дві пари кутів є конгруентними, оскільки лінії паралельні. Ще більш тривіально конгруентні фігури схожі із загальним співвідношенням\(r=1\).
Якщо два трикутника такі, що співвідношення між двома його сторонами однакові, а кути між цими двома парами сторін є конгруентними, то трикутники подібні.
Доказ: По-перше, це виглядає так, що наша пропорція неправильна, оскільки це говорить про співвідношення двох сторін одного трикутника замість наявності константи пропорційності для відповідності (довжина сторони зображення до вихідної довжини сторони). Цей факт обумовлений властивістю звичайних фракцій:
\(a / b=x / y\)якщо\(a / x=b / y\) їх взаємні згодні; т\(x / a=y / b\). Е.
Тут придумайте\(x\) як довжину зображення стороною довжини\(a\),\(y\) так і аналогічно для\(b\), і під відповідність, яка, сподіваємося, виявиться відповідність подібності. \(r\)Дозволяти бути, що загальне співвідношення; тобто,\(r=x / a\) або\(x=r a\) і\(y=r\) б., Буде доведено, що\(r>0\), для будь-якого, інші 2 кути також конгруентні і треті сторони знаходяться в тому ж співвідношенні\(\mathrm{r}\). Доказ базується на індукції\(\mathrm{r}=\mathrm{n}\) як натуральних чисел, так і простих дробів\(r=1 / n\) з новим трикутником з двома сторонами і включеним кутом, накладеним на оригінал\(\triangle \mathrm{ABC}\) (SAS для конгруентних трикутників) з двома сторонами довжини \(\mathrm{r}(\mathrm{AB})\)і\(r(\mathrm{AB})\).
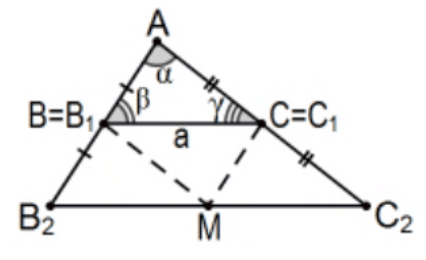
\(\mathrm{r}=1\)Випадок: Це просто конгруентність SAS, як згадувалося вище.
Кейс\(\mathrm{r}=2\): Це лише безпосередній наслідок останньої теореми. Для того, щоб підготуватися до доказу за допомогою математичної індукції, ми перейменуємо вершини, як показано на малюнку, з середніми точками\(\mathrm{B}=\mathrm{B}_{1}\) та\(\mathrm{C}=\mathrm{C}_{1}\) складанням довжин\(\mathrm{AB}_{2}=2 \mathrm{AB}\) і\(\mathrm{AC}_{2}=2 \mathrm{AC}\). За останньою теоремою, довжина\(\mathrm{B}_{2} \mathrm{C}_{2}=2 \mathrm{~B}_{1} \mathrm{C}_{1}\) і лінія\(\mathrm{B}_{2} \mathrm{C}_{2}\) паралельна лінії,\(\mathrm{B}_{1} \mathrm{C}_{1}\) що підтверджує\(\angle \mathrm{AB}_{1} \mathrm{C}_{1} \cong \angle \mathrm{AB}_{2} \mathrm{C}_{2}\) і\(\angle \mathrm{AC}_{1} \mathrm{~B}_{1} \cong \angle \mathrm{AC}_{2} \mathrm{~B}_{2}\). Дозволяючи\(M_{2}\) бути серединою сегмента\(B_{2} C_{2}\) визначає 3 нові трикутники, які збігаються з оригінальними\(\triangle A B C\),\(4=2^{2}\) конгруентними трикутниками.
\(r=1 / 2\)Випадок: Цього разу поміняйте початковий трикутник\(B=B_{2}\)\(A B_{1}=(1 / 2) A B\) і\(C=C_{2}\) роблячи довжини та\(\mathrm{AC}_{1}=(1 / 2) \mathrm{AC}\) середню ситуацію мотивуючої теореми вище.
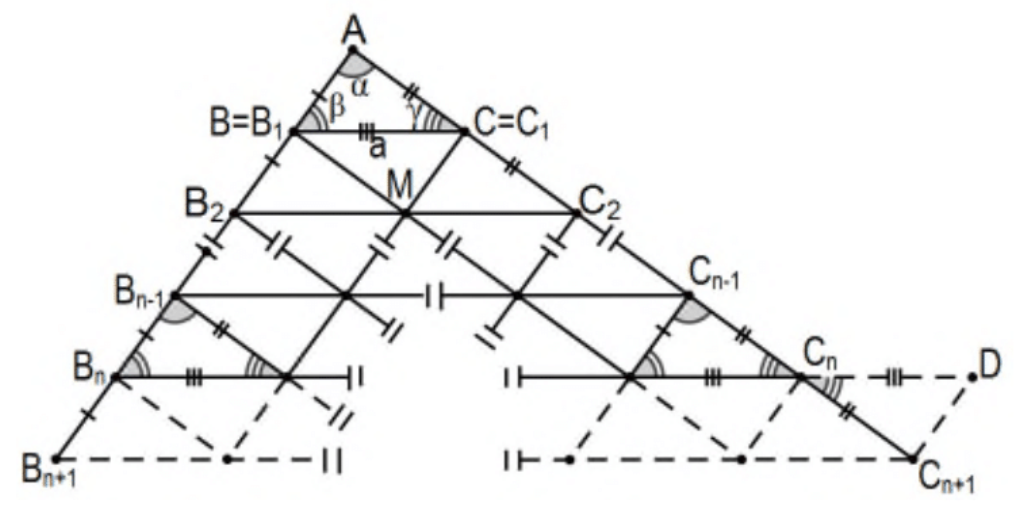
\(r=n\)Випадок: Для\(n\) будь-якого додатного цілого числа, indut\(n\) далі випадку\(r=2\) наступним чином:
Припустимо, що результат (схожість\(\mathrm{r}=\mathrm{n}\) із загальним коефіцієнтом з\(\mathrm{n}^{2}\) внутрішніми конгруентними трикутниками) є дійсним для\(r=2,3, \ldots, n\) будь-якого трикутника\(\triangle \mathrm{AB}_{\mathrm{n}+1} \mathrm{C}_{\mathrm{n}+1}\) з довжиною\(\mathrm{AB}_{\mathrm{n}+1}=(\mathrm{n}+1) \mathrm{AB}\)\(\mathrm{AC}_{\mathrm{n}+1}=(\mathrm{n}+1) \mathrm{AC}\), довжиною, і, для зручності, той же LA. За Постулатом Лінійки визначте n точок, щоб визначити\(n+1\) конгруентні сегменти уздовж кожного сегмента\(\mathrm{AB}_{\mathrm{n}+1}\) та\(\mathrm{AC}_{\mathrm{n}+1}\) за індексним номером та застосувати індуктивну гіпотезу до\(\triangle \mathrm{AB}_{\mathrm{n}} \mathrm{C}_{\mathrm{n}}\). Після доказу попередньої теореми, продовжити відрізок\(B_{n} C_{n}\) довжини\(n B C\) за індуктивною гіпотезою, відрізок довжини,\(B C\) щоб визначити точку\(D\) та розглянути\(\Delta C_{n+1} D C_{n}\). Цей трикутник конгруентний оригіналу,\(\Delta C_{n+1} C_{n} D \cong \Delta A C B\) від SAS. За cpctc сегментів і кутів і перехідності,\(\mathrm{DC}_{n+1} \cong \mathrm{B}_{\mathrm{n}} \mathrm{B}_{\mathrm{n}+1}\) і їх лінії паралельні тому чотирикутник\(\mathrm{B}_{\mathrm{n}} \mathrm{B}_{n+1} C_{n+1} \mathrm{D}\) має пару протилежних сторін, які є одночасно конгруентними і паралельними, так що це паралелограм (PS 4, #15) і його інша пара протилежних сторін також конгруентні і паралельний\((\mathrm{PS} 4, \# 12)\). Оскільки\(\mathrm{B}_{\mathrm{n}} \mathrm{D}\) має довжину\(\mathrm{nBC}+\mathrm{BC}=(\mathrm{n}+1) \mathrm{BC}\), потрібна сторона\(\mathrm{B}_{\mathrm{n}+1} C_{\mathrm{n}+1}\) також разом з відповідною конгруентністю кутів на\(\mathrm{B}_{\mathrm{n}+1}\) і\(\mathrm{C}_{\mathrm{n}+1}\) підтверджує схожість с\(\Delta \mathrm{ABC}\). Нарешті, підраховуючи кількість внутрішніх конгруентних трикутників, ми маємо оригінальні\(n^{2}\) плюс\(n+1\) нові, орієнтовані з ними\(\triangle \mathrm{ABC}\) та\(n\) між ними, орієнтованими догори ногами:\(n^{2}+(n+1)+n=n^{2}+2 n+1=(n+1)^{2}\) а індуктивний крок є повний. (Для кращого розуміння уважно стежте за доказом\(n=3\); ідеї точно такі ж.)
Випадок\(\mathrm{r}=1 / \mathrm{n}\): Для будь-якого додатного цілого числа\(\mathrm{n}\) та двох трикутників, які задовольняють SAS для умов подібності із загальним співвідношенням\(\mathrm{r}=1 / \mathrm{n}\) (одна пара конгруентних кутів і там, включаючи пари сторін у однаковому\(1 / \mathrm{n}\) співвідношенні), розділіть кожну з включаючи сторони великого трикутника, скажімо,\(\triangle \mathrm{ABC}\) у\(\mathrm{n}\) конгруентні відрізки (Постулат лінійки) та індексуйте їх як з доказом будь-якого натурального числа\(r=n ;\), яке є\(B_{n}=B\)\(C_{n}=C\) і кожної точки з них підрозділи як\(\mathrm{B}_{\mathrm{i}}\) і\(\mathrm{C}_{\mathrm{i}}\) попутно. Тоді\(\mathrm{SAS}\) Конгруентність, менший з трикутників конгруентний,\(\Delta \mathrm{AB}_{1} \mathrm{C}_{1}\) починаючи з якого ми можемо відновити схожість з\(\Delta \mathrm{ABC}\) оригіналом у випадку\(r=n\).
\(r=m / n:\)Випадок Для будь-якого додатного раціонального числа: У цьому випадку почніть або з чисельника, або знаменника і послідовно застосуйте відповідні відмінки.
Випадок\(\mathrm{r}:\) Для будь-якого позитивного дійсного числа\(\mathrm{r}:\) Якщо\(\mathrm{r}\) є раціональним, це вже зроблено так припустимо, що\(\mathrm{r}\) це ірраціонально. Розглянемо будь-яку послідовність позитивних раціональних чисел, яка сходиться до\(r\) і використовувати безперервність. \(Q E D\)
Якщо два трикутника такі, що співвідношення між усіма трьома парами відповідних їм сторін однакове, то трикутники аналогічні.
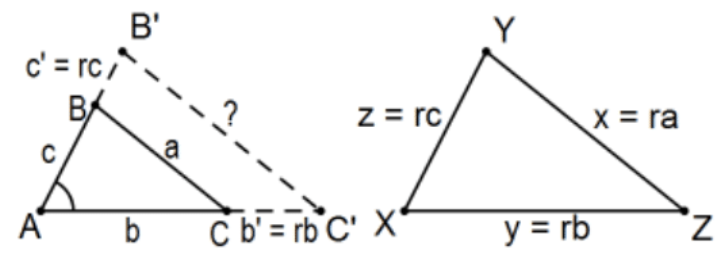
Доказ: Тут постійною пропорційності для кореспонденції є те загальне співвідношення\(r\). Можна було б почати з нуля, як у доказах подібності SAS, але це не обов'язково. Виберіть дві сторони першого трикутника і розгляньте трикутник, утворений кутом між ними, але з двома сторонами r разів довше. За SAS Подібність, третя сторона цього трикутника в\(r\) рази первісна третя сторона, ра. Але потім, за Конгруенцією SSS,... КАД.
Якщо два трикутника такі, що два його кута конгруентні, то трикутники схожі.
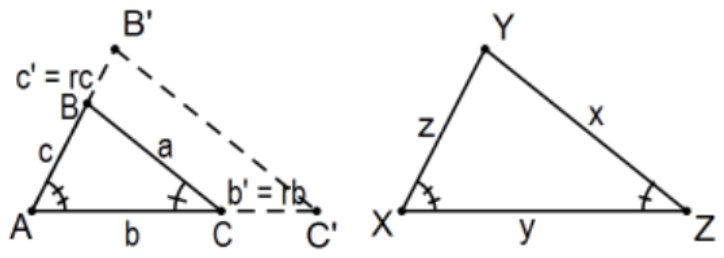
Доказ: Де константа пропорційності для листування? Це відношення r сторін, включених двома парами конгруентних кутів,\(r=y / b\).
Оскільки розглядається тільки одна пара сторін, «вони» всі згодні і діють так, як і з ССС, як зазначено вище. Більш явно, припустимо\(\triangle \mathrm{ABC}\) і\(\triangle \mathrm{XYZ}\) є такими, що\(\angle \mathrm{A} \cong \angle \mathrm{X}\) і\(\angle \mathrm{C} \cong \angle \mathrm{Z}\) як зазначено. Помноживши 2 сторони\(\angle A\) на один і той же коефіцієнт\(r\)\(\mathrm{r}>0\), ми маємо схожі трикутники\(\triangle \mathrm{ABC} \sim \triangle \mathrm{AB}^{\prime} \mathrm{C}^{\prime}\) за\(\mathrm{SAS}\) схожістю. За визначенням подібності,\(\angle \mathrm{C}^{\prime} \cong \angle \mathrm{C}\) так, по транзитивності,\(\angle \mathrm{C}^{\prime} \cong \angle \mathrm{Z}\) і ми маємо\(\triangle \mathrm{AB}{ }^{\prime} \mathrm{C}^{\prime} \cong \triangle \mathrm{X} \mathrm{YZ}\) по ASA конгруентність. Нарешті,\(\triangle \mathrm{ABC} \sim \triangle \mathrm{XYZ}\) по транзитивності.
Висота від прямого кута прямокутного трикутника ділить трикутник на два трикутника, кожен аналогічний оригіналу.
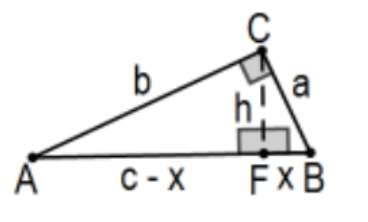
Доказ: Гострі кути прямокутного трикутника є доповнюючими, тому результат є негайним за подібністю AA. КАД.
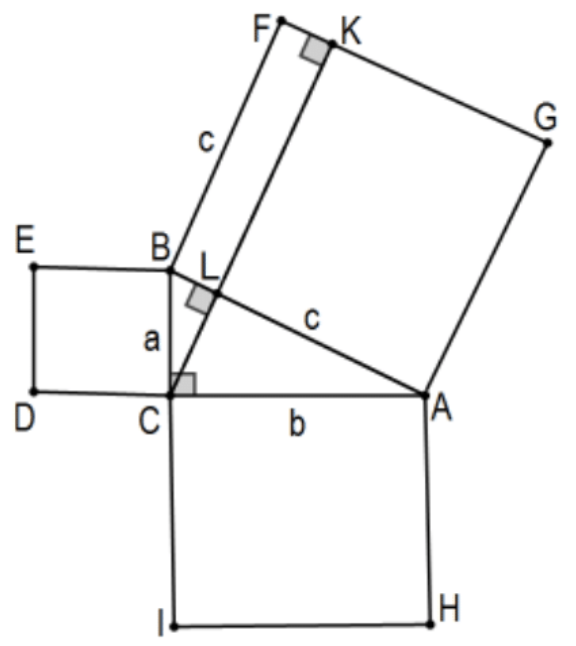
Доказ 4: Цей факт дає серце ще одного доказу теореми Піфагора; приємно тим, що вона має традиційну картину, але з набагато простішим доказом. Починаючи як і раніше\(\triangle \mathrm{ABC}\) з правого з квадрата з кожного боку, візьміть лінію на вершині прямого кута\(C\) перпендикулярно гіпотенузі так, що\(\mathrm{CL}\) це висота від прямого кута вправо\(\triangle \mathrm{ABC}\). Це означає, що\(\mathrm{BL} / \mathrm{a}=\mathrm{a} / \mathrm{c}\) так\(\mathrm{c}(\mathrm{BL})=\mathrm{a}^{2}\). Тобто площа квадрата\(\mathrm{BCDE}\) - це площа прямокутника БФКЛ. \(\mathrm{b}^{2}\)Аналогічно виглядає площа прямокутника АГКЛ. КАД. (див.\(\operatorname{PS} 4, \# 21)\)
[Більш чітко, довжини відрізків 2 поперек до 3 (або більше) паралельних ліній пропорційні (мають однакові співвідношення)].
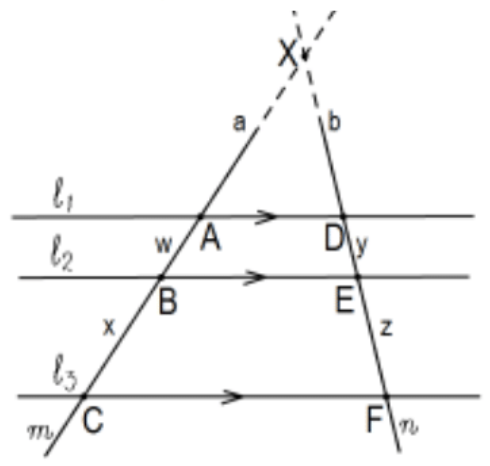
Доказ: На малюнку 3 лінії і\(l_{3}\) є паралельними лініями\(\ell_{1}, l_{2}\), вирізаними поперечками\(m\) і\(n\). Потрібно показати, що визначені відрізки пропорційні; тобто показати, що\(w / x=y / z\).
Якщо\(n\) поперечні\(m\) і паралельні, то визначені чотирикутники паралелограми так\(\mathrm{w}=\mathrm{y}\) і\(\mathrm{x}=\mathrm{z}\) і тривіальна рівність співвідношень так припускають, що вони перетинаються. Дозволяти X бути перетином\(m\) і\(n\). Це визначає 3 трикутника, всі схожі за подібністю AA. Рівність бажаних співвідношень випливає з прямого застосування співвідношень подібності цих трикутників. Деталі залишені як PS 4, #18.
Побудувати: добуток і частка двох відрізків лінії.
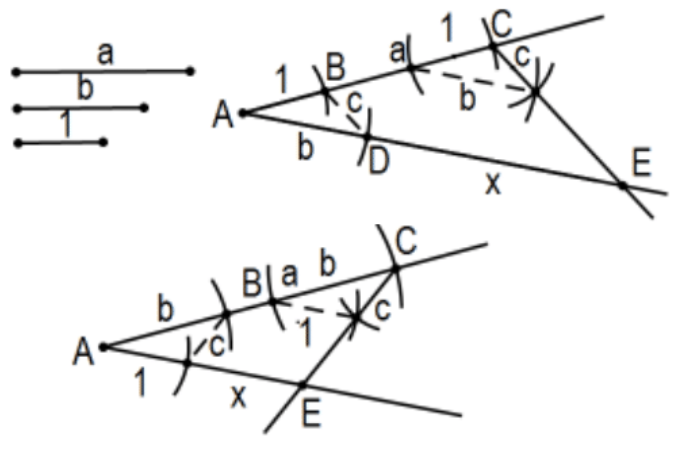
Більш конкретно, задані відрізки прямої довжини a\(b\), і одиниці довжини 1, будують відрізки довжини ab і\(a / b\). І\(\mathrm{D}\) як зазначено на малюнку визначає\(\triangle \mathrm{ABD}\). Скопіюйте\(\angle \mathrm{B}\) в точці\(\mathrm{C}\), як зазначено, щоб визначити точку\(\mathrm{E}\) на іншому промені. Потім\(\mathrm{x}\), довжина відрізка\(\mathrm{DE}\), є необхідною довжиною,\(x=a b\). Для a/b це та сама конструкція, за винятком початку з b, за яким слідує a на одному промені та 1 на іншому промені.
Доказ: За конструкцією\(\angle \mathrm{ABD} \cong \angle \mathrm{ACE}\) і конгруентними відповідними кутами мається на увазі, що лінії CE і BD паралельні. Так як паралельні лінії відрізають пропорційні відрізки,\(1 / b=a / x\). Тому\(x=a b\).
Теорема: Бісектриса кута трикутника ділить протилежну сторону пропорційно сторонам кута.
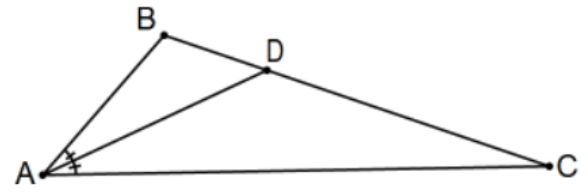
Тобто в пов'язаній фігурі, якщо промінь\(\mathrm{AD}\) є бісектрисою\(\angle A\), то\(\mathrm{AB} / \mathrm{AC}=\mathrm{DB} / \mathrm{DC}\).
Доказ: Дозвольте\(\mathrm{E}\) бути перетином лінії змінного струму з лінією на\(\mathrm{B}\) паралельній лінії\(\mathrm{AD}\) і розглянемо створений трикутник:\(\triangle \mathrm{DCA} \sim \triangle \mathrm{BCE}\). КАД.
Наслідок: Бісектриса кута трикутника є медіаною тоді і тільки тоді, коли трикутник рівнобедрений.
Теорема: Теорема про вписаний кут: Кут, вписаний у коло, вимірює половину міри його перехопленої (піднесеної) дуги; тобто половину відповідного центрального кута.
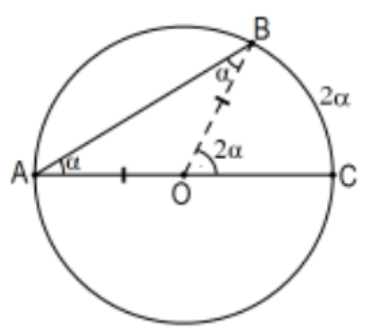
Доказ: У всіх випадках вершина\(A\) знаходиться на колі з центром в\(O\).
Випадок 1: Одна сторона кута - це діаметр. При цьому центральний кут - це саме зовнішній кут рівнобедреного трикутника, який визначається вписаним кутом. Явно, оскільки\(\mathrm{OA}\) і\(\mathrm{OB}\) є радіусами одного і того ж кола,\(\triangle \mathrm{AOB}\) є рівнобедреним і його базові кути (в\(A\) і\(B\)) конгруентні так, що їх сума вдвічі\(\alpha=m(\angle A)\). За евклідової формою EAT,\(2 \alpha=2 \mathrm{~m}(\angle \mathrm{A})=\mathrm{m}(\angle \mathrm{BOC})\). Оскільки міра дуги визначається як міра центрального кута, який підпорядковує його, твердження доведено.
Випадок 2: Центр кола знаходиться всередині кута. Включити діаметр OD:\(2 \alpha=2\left(\alpha_{1}+\alpha_{2}\right)=2 \alpha_{1}+2 \alpha_{2}\).
Випадок 3: Центр кола зовнішній до кута.
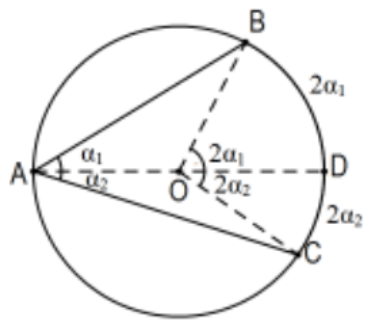
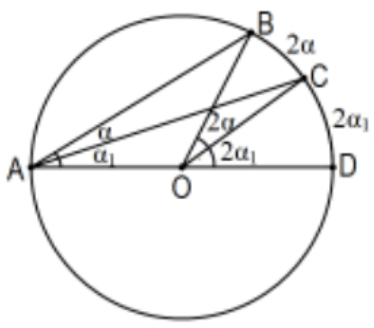
Зауважте, що\(\angle B A C=\angle B A D-\angle C A D\). Це означає, що\(2 \alpha=2\left(\left(\alpha+\alpha_{1}\right)-\alpha_{1}\right)=2\left(\alpha+\alpha_{1}\right)-2 \alpha_{1}\).
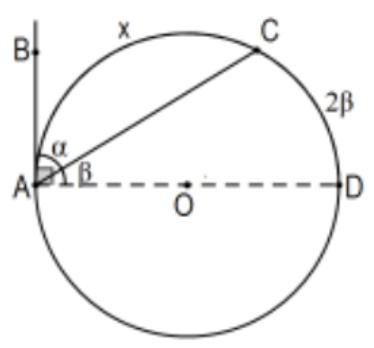
Випадок 4: Одна сторона кута дотична до кола. Припустімо,\(\mathrm{AB}\) що лінія дотична до кола в\(\mathrm{A}\), і\(\angle B A C\) це гостро. Розглянемо\(\angle C A D\), додатковий кут з діаметром\(\mathrm{AD}\) визначається радіусом,\(\mathrm{OA}\) так як, за попередньою теоремою, лінії\(\mathrm{AB}\) і\(\mathrm{AD}\) є перпендикулярними. Очевидно, що міра дуги змінного струму\(\mathrm{x}=180^{\circ}-\mathrm{m}(\operatorname{arc} \mathrm{CD})\) так, у випадку 1,\(x=180^{\circ}-2 \beta=2\left(90^{\circ}-\beta\right)=2 \alpha\) і ми закінчили. Якщо\(\angle B A C\) тупий, його доповнення гостре, тому використовуйте гострий випадок і відніміть від\(360^{\circ}\).
Слідство: Трикутник, вписаний півколом (тобто одна сторона - діаметр) - це прямокутний трикутник.
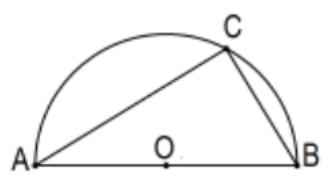
Історично цей факт відомий як теорема Фалеса. Фалес був філософ-математик, який жив приблизно 300 років до Евкліда і був названий першим філософом грецької традиції.
Наслідок: Побудувати дотичні від точки поза колом до кола.
[Примітка: Це був PS 2, #25, в нейтральній геометрії. Навіщо робити це знову? Ця конструкція є тією, яку зазвичай навчають, тому набагато відоміша, ніж попередня. Ця ситуація трохи дивна, оскільки обидві конструкції знаходяться в оригіналі Евкліда, Книга III, нейтральна геометрія легше довести, і наведена раніше (Prop. 17 проти Prop. 31). Однак це робить приємний приклад ситуації, коли зміна аксіом залишає пропозицію істинним (здатність будувати дотичні), але наведена тут евклідова форма не є дійсною в нейтральній геометрії. Етапи будівництва можна зробити, але не тільки доказ не вдається, він ніколи не виробляє фактичних дотичних!]
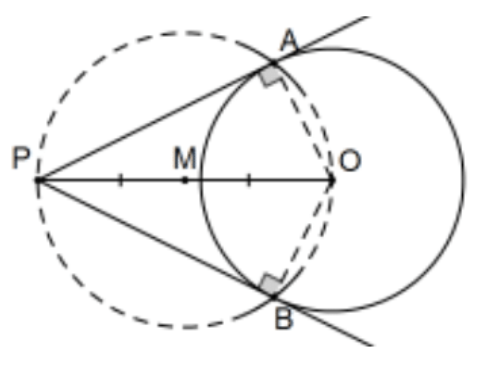
Побудова: Бісекція відрізка, визначеного точкою та центром кола, і розгляньте коло, центроване в цій точці, радіусом, визначеним будь-якою з цих точок, (M; MO). Її перетину з колом є точками дотику. Більш явно, (якщо центр кола не задано) побудувати центр кола, середину\(\mathrm{M}\) відрізка лінії PO\(\mathrm{O}\), і коло з центром в M і радіусом MP = MO. Допускаючи\(A\) і\(B\) бути точками перетину цього кола з вихідним колом, лінії ПА і ПБ є бажаними дотичними.
Доказ: Це безпосередньо від теореми про трикутники, вписані в півкола. КАД.
Теорема: Побудувати відрізок прямої довжини квадратного кореня довжини відрізка:
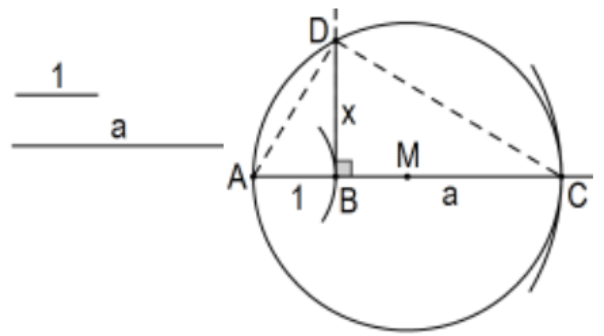
Рішення: Задані відрізки одиничної довжини та довжини a\(M\), побудувати середину відрізка довжини\(1+\mathrm{a},(\mathrm{AB}+\mathrm{BC}=\mathrm{AC}\) на малюнку\()\) та окружність\(M\) з центром радіуса\(M C\). Нарешті, побудуйте перпендикуляр у точці\(B\), щоб визначити точку\(D\). Тоді сегмент БД є необхідним сегментом.
Доказ: Це трикутник, вписаний у півколо, так\(\triangle \mathrm{ACD}\) це прямокутний трикутник і\(\mathrm{BD}\) висота від прямого кута так\(\triangle \mathrm{ADB} \sim \triangle \mathrm{DCB}\) і у нас\(x / 1=a / x\) так що\(x^{2}=a\) або\(x=\sqrt{a}\). КАД.
Теорема: Побудувати середнє геометричне довжин двох відрізків лінії:
Тобто, задані відрізки довжин а і\(b\), вирішують:\(x^{2}=a b\) геометрично.
Рішення: Почніть з\(\mathrm{m}(\mathrm{AB})=\mathrm{a}\) і\(\mathrm{m}(\mathrm{BC})=\mathrm{b}\) на малюнку вище. КАД.
Побудувати всі позитивні розв'язки квадратного рівняння: Тобто, якщо a, b і c є конструктивними, а рівняння має реальні розв'язки, вирішуйте\(a x^{2}+b x+c=0\) геометрично.
Рішення: Для\(a x^{2}+b x+c=0, a \neq 0\), нагадаємо, що квадратична формула дає свої рішення:
\(x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \quad\)Кожен крок алгоритму є конструктивним. КАД.
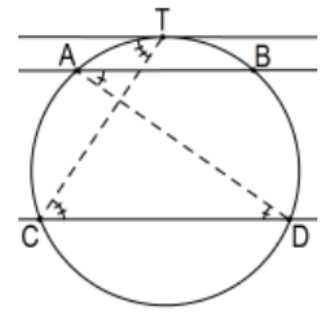
Теорема: Паралельні лінії, що перетинають коло, визначають конгруентні дуги.
Доказ: Це безпосередньо від теореми про вписаний кут.
Примітка: Існує проблема в тому, що ми ніколи не обговорювали, що навіть означає конгруентні дуги; все було з точки зору розбиття фігури на конгруентні трикутники, що неможливо для дуг кіл. Очевидно, що конгруентні кола - це ті, що мають конгруентні радіуси. Для конгруентних дуг ми маємо на увазі дуги конгруентних кіл, які визначають конгруентні центральні кути або еквівалентно (по конгруентності трикутників SAS) конгруентні хорди.
[Примітка: Це НЕ вірно в гіперболічній геометрії: (Дуга Пуанкаре: DC\(\cong \mathrm{AB}<\mathrm{EB}\)).]
Теорема: Теорема хорди: Для точки всередині кола добуток довжин відрізків, визначених на будь-якій хорді через неї,\(w x=y z\) є постійним (тобто на малюнку), а міра кута, визначеного двома хордами через точку, становить половину суми його перехопленого (підтягнуті) дуги.
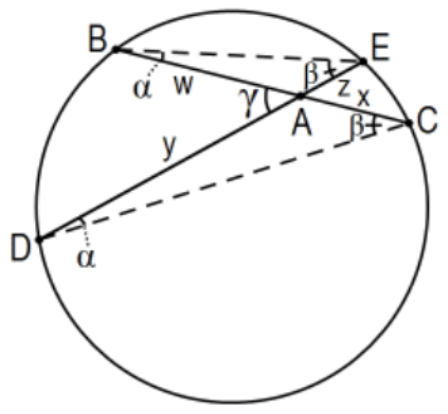
Доказ: За теоремою про вписаний кут,\(\angle \mathrm{E} \cong \angle \mathrm{C}\) і\(\angle \mathrm{B} \cong \angle \mathrm{D}\) так, по AA подібності,\(\triangle \mathrm{ABE} \sim \triangle \mathrm{ADC}\) так\(\mathrm{AB} / \mathrm{AD}=\mathrm{AE} / \mathrm{AC}\) чи\(\mathrm{w} / \mathrm{y}=\mathrm{z} / \mathrm{x}\). Нарешті,\(\mathrm{wx}=\mathrm{yz}\). Для кутів,\(\mathrm{m}(\angle \mathrm{BAD})=\mathrm{m}(\angle \mathrm{ABE})+\mathrm{m}(\angle \mathrm{AEB})\) за евклідовою формою EAT та використовуйте теорему про вписаний кут, щоб висловити\(\mathrm{m}(\angle \mathrm{ABE})\) та\(\mathrm{m}(\angle \mathrm{AEB})\) через дугові міри їх підтенених дуг. КАД.
Для точки за межами кола добуток довжин зовнішнього відрізка на всю його січну (зовнішній сегмент плюс хорда) є постійним, а в дотичному випадку ця константа - це лише квадрат довжини відрізка. Міра кута в точці, визначеній двома секантами, становить половину різниці підтягнутих дуг. Тобто і як на фото, включаючи дотичний випадок,\(\mathrm{w}(\mathrm{w}+\mathrm{x})=\mathrm{y}(\mathrm{y}+\mathrm{z})=\mathrm{t}^{2}\).
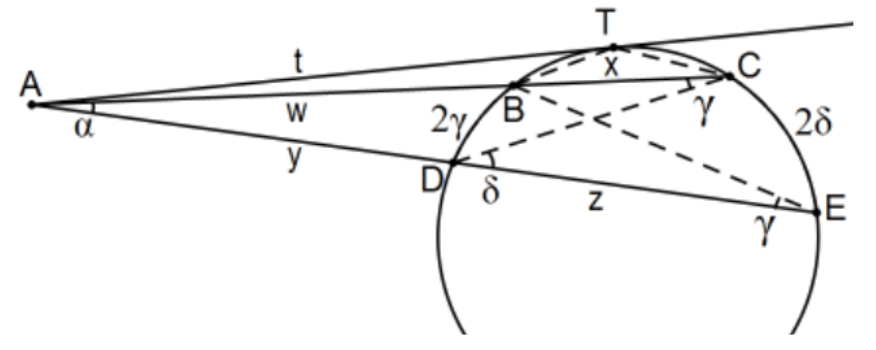
Доказ: Кут під\(A\) загальним і, відповідно до теореми про вписаний кут,\(\angle C \cong \angle \mathrm{E}\) тому ми маємо\(\triangle \mathrm{ABE} \sim \triangle \mathrm{ADC}\) подібність AA. За постійним добутком висновок\(\mathrm{AB} / \mathrm{AE}=\mathrm{AD} / \mathrm{AC}\) і перехресне множення. Для кутів використовуйте евклідієву форму\(\mathrm{ETA}, \mathrm{m}(\angle \mathrm{CDE})=\mathrm{m}(\angle \mathrm{DAC})+\mathrm{m}(\angle \mathrm{DCA})\),\(\delta=\alpha+\gamma\) або\(\alpha=\delta-\gamma\). Тепер теорема про вписаний кут з дугами\(C E\) і BD, ми маємо\(\delta=(1 / 2)(\mathrm{m}(\mathrm{CE})-\mathrm{m}(\mathrm{BD}))\). Щодо дотичного випадку див.\(\mathrm{PS} 4, \# 7\) QED.
Ще в главі 1 ми навчилися будувати центр кола в нейтральній геометрії; а саме, вибрати будь-які три точки кола і перпендикулярні бісектриси будь-яких двох хорд, визначених перетином, щоб визначити центр кола. Ця конструкція була знайома багатьом з вас як конструкція для окружності трикутника. Тобто побудувати перпендикулярні бісектриси двох сторін трикутника, щоб визначити окружність, а відрізок від цієї точки до будь-якої з його вершин - це його радіус. Ми побачили в главі 3, що він не є дійсним в нейтральній геометрії, оскільки це помилково в гіперболічній геометрії; тобто ми знаємо, що деякі трикутники не мають окружності, оскільки іноді ці перпендикулярні бісектриси не перетинаються. У евклідовому випадку неможливість перетину означала б, що обидві обрані сторони були частиною однієї лінії, так що трикутник був не трикутником, а так званим «виродженим» трикутником; тобто три колінеарні точки. Однак багатокутники з більш ніж трьома сторонами не настільки чіткі; зазвичай багатокутник не має окружності, але існує дивовижна характеристика для чотирикутників:
Чотирикутник має окружність тоді і тільки тоді, коли кожна пара протилежних кутів має суму\(180^{\circ}\).
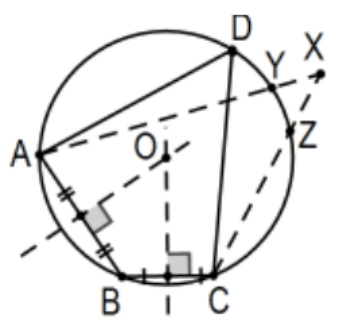
Доказ: Теорема про вписаний кут відразу означає, що якщо чотирикутник може бути вписаний в коло, протилежні кути повинні додати до\(180^{\circ}\). І навпаки, припустимо, що у нас є чотирикутник з протилежними кутами, які додають до\(180^{\circ}\). Використовуйте будь-які три вершини для побудови окружності цього трикутника, трикутник ці три точки визначають і доводять, що четверта вершина повинна лежати на ній, а також. По суті, теорема хорди (якби точка була всередині) та секантна теорема (якщо точка була зовні) означали б, що сума кута була б неправильною. Деталі залишаються як Ex\(30.\)
Побудова: добуток і частка двох відрізків прямої з використанням теореми хорди:
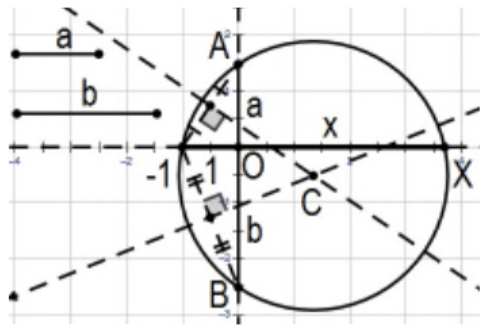
Альтернативна побудова для добутку (і для частки) довжин двох відрізків лінії заданої довжини полягає в тому, що починається з будь-яких двох пересічних ліній як ліній їх кінцевих акорд з побудованою сумою відрізків від перетину ліній як однієї з хорд і a відрізок одиниці довжини від цієї точки як один відрізок іншої хорди. Це визначає 3 точки потрібного кола і використовуйте їх для побудови визначеного кола. Довжина відрізка від точки перетину до кола - бажана довжина (PS 4, #31). [Примітка: Використовуючи\(x\)\(y\) осі та як лінії акорди та довжини, як показано на малюнку, продукт може бути безпосередньо «зчитувати"' позитивну\(x\) вісь\((\sim(3 / 2)(5 / 2)=15 / 4).]\)