Skip to main content
LibreTexts - Ukrayinska

5.3: Теореми гіперболічної геометрії

  1. Last updated
  2. Save as PDF
  • Page ID
    58455

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Зверніть увагу, що при роботі над цими проблемами модель може бути корисною для з'ясування того, чому щось працює. Однак докази повинні бути безпосередньо засновані на аксіомах. Законно довести твердження за допомогою опису моделі, якщо модель була доведена як еквівалентна аксіомам. Для цього звичайно докази використання моделі будуть коштувати менше балів, ніж докази безпосередньо з аксіом.

    Лемма: Гіперболічний паралельний наслідок

    З огляду на пряму і точку, яка не знаходиться на цій лінії, існує нескінченно багато ліній через цю точку паралельно заданій лінії.

    Лема: Відчувається Паралель

    Враховуючи пряму і точку, яка не знаходиться на цій лінії, існує перша лінія через цю точку паралельно заданій лінії.

    Визначення: Сенсована паралель

    Лінія - це чутлива паралель тоді і лише тоді, коли вона є першою лінією, паралельною заданій лінії на цій стороні через задану точку.

    Визначення: Кут паралелізму

    Менший кут, утворений чутливою паралеллю і поперечним через задану точку, є кутом паралелізму тоді і тільки тоді, коли поперечний перпендикулярний заданій прямій.

    Слідство: Термін

    Кут паралельності однаковий зліва і справа.

    Теорема

    Кут паралельності менше π/2.

    Лемма

    Розглянемо наступне, проілюстроване в.\(\PageIndex{1}\) тоді відчувається паралель повинна бути вище SA праворуч від А і вище UA.

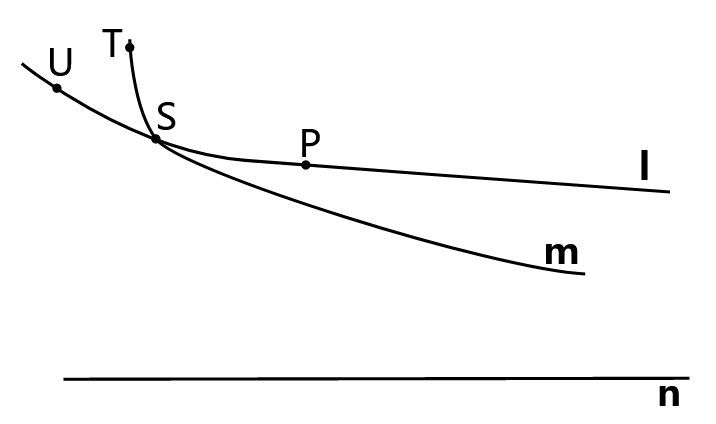
    5.3.1.jpg
    Малюнок\(\PageIndex{1}\): Відчуті паралелі ліворуч

    Лемма: Термін

    Розглянемо наступне, проілюстроване в.\(\PageIndex{2}\)

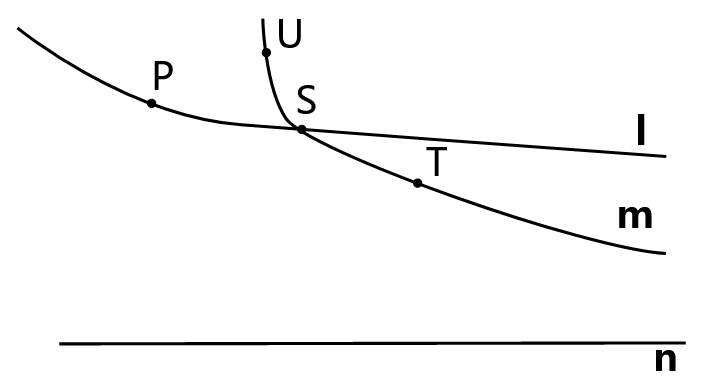
    5.3.2.png
    Малюнок\(\PageIndex{2}\): Відчуті паралелі праворуч

    Лемма

    Якщо - це право, що відчувається паралельно m при P, то - це право, що відчувається паралельно m в будь-якій точці ліворуч від P на.

    Теорема: Відчувається скрізь

    Якщо - це відчувається паралельно m в точці P, то - це відчувається паралельно m в будь-якій точці Q також на.

    Визначення: Трикутник Омега

    Пара паралельних ліній і поперечна є трикутником омега тоді і тільки тоді, коли паралелі відчуваються паралелі.

    Намалюйте трикутник омега за допомогою моделі диска Пуанкаре.

    Лема: Перекладина для трикутників Омега

    Якщо рядок k містить вершину та внутрішню точку трикутника омега, вона перетинає сторону, протилежну вершині.

    Чи працює версія Аксіоми Паша для трикутників омега? Нехай і m відчуваються паралелі. Дозволяти AB бути поперечним з Aі Bm Дозволяти M бути серединою AB, а D - підніжжя перпендикуляра від M до. Також вибирайте Fm на протилежній стороні AB від D такий, що BFAD Нехай Cñ бути таким, що C-A-D. Доведіть, що CABabΩ.

    Лема: Зовнішній кут трикутника Омега

    Зовнішній кут трикутника омега більше, ніж протилежний внутрішній кут.

    Лема: Кутова сторона Конгруентність

    Два трикутника омега є конгруентними, якщо довжина скінченних сторін і міра однієї пари відповідних кутів конгруентні.

    Лема: Кут Конгруентність

    Два трикутника омега є конгруентними, якщо відповідні пари кутів конгруентні.