17.3: Будівництво Боляя

Last updated
Save as PDF

Page ID: 59075

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Припустімо, що нам потрібно побудувати лінію через$P$ асимптотично паралельну заданій лінії$\ell$ в h-площині.

Якщо$A$ і$B$ є ідеальними точками$\ell$ в проективній моделі, то ми могли б просто провести евклідову лінію$(PA)$. Однак ідеальні точки не лежать в h-площині, тому немає можливості використовувати їх у будівництві.

У наступній конструкції ми припускаємо, що ви знаєте конструкцію компаса і лінійки перпендикулярної лінії; див. Вправа 5.22.

Теорема$\PageIndex{1}$ Bolyai's construction

Відкиньте перпендикуляр від$P$ до$\ell$; позначте його символом$m$. $Q$Дозволяти бути точкою стопи$P$ на$\ell$.
Звести перпендикуляр від$P$ до$m$; позначити його по$n$.
Позначте$R$ точкою на$\ell$ відмінному від$Q$.
Відкиньте перпендикуляр від$R$ до$n$; позначте його символом$k$.
Намалюйте коло$\Gamma$ з центром$P$ і радіусом$QR$. Відзначте$T$ точкою перетину$\Gamma$ с$k$.
Лінія$(PT)_h$ асимптотично паралельна$\ell$.

Вправа$\PageIndex{1}$

Поясніть, що станеться, якщо виконати конструкцію Боляя в евклідовій площині.

Відповідь: Додайте сюди тексти. Не видаляйте цей текст спочатку.

Щоб довести, що конструкція Боляя дає асимптотично паралельну пряму в h-площині, достатньо показати наступне:

Теорема$\PageIndex{1}$

Припустимо$P$$Q$,$R$,$S$,$T$ бути точки в h-площині такі, що

$S\in (RT)_h$,
$(PQ)_h\perp (QR)_h$,
$(PS)_h\perp(PQ)_h$,
$(RT)_h\perp (PS)_h$і
$(PT)_h$і$(QR)_h$ асимптотично паралельні.

Потім$QR_h=PT_h$.

Доказ

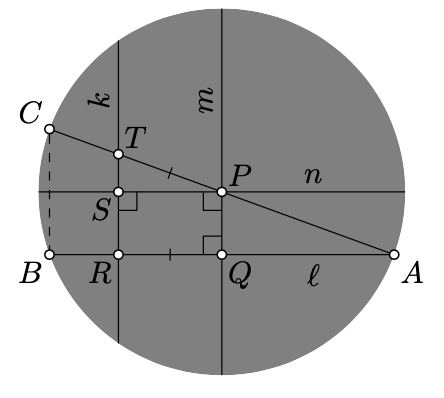
Ми будемо використовувати проективну модель. Без втрати спільності можна вважати, що$P$ це центр абсолюту. Як було зазначено на сторінці, в даному випадку відповідні евклідові лінії також перпендикулярні; тобто$(PQ)\perp (QR)$,$(PS)\perp(PQ)$, і$(RT) \perp (PS)$.

$A$Дозволяти бути загальною ідеальною точкою$(QR)_h$ і$(PT)_h$. Нехай$B$ і$C$ позначимо залишилися ідеальні точки$(QR)_h$ і$(PT)_h$ відповідно.

Зверніть увагу, що евклідові лінії$(PQ)$$(TR)$, і$(CB)$ паралельні.

$2021-03-01 пнг$

Тому

Зокрема,

$\dfrac{AC}{AB}=\dfrac{AT}{AR}=\dfrac{AP}{AQ}.$

Звідси випливає, що

Зокрема,$\dfrac{AT\cdot CP}{TC\cdot PA}=\dfrac{AR\cdot BQ}{RB\cdot QA}$. Застосовуючи формулу для h-відстані 17.2.1, отримаємо це$QR_h=PT_h$.

Теорема\(\PageIndex{1}\) Bolyai's construction

Вправа\(\PageIndex{1}\)

Теорема\(\PageIndex{1}\)