15.4: Перспективна проекція

Last updated
Save as PDF

Page ID: 59162

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Розглянемо дві площини$\Pi$ і$\Pi'$ в евклідовому просторі. Дозвольте$O$ бути точкою, яка не належить ні до$\Pi$ ні$\Pi'$.

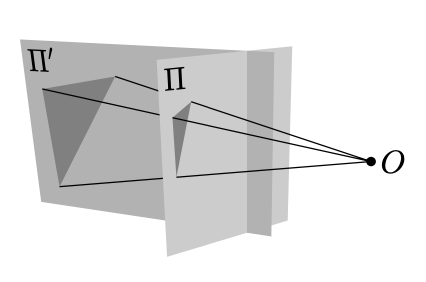
$2021-02-25 пнг$

Перспективна проекція від$\Pi$ до$\Pi'$ з центром на$O$ відображає точку$P\in \Pi$ на точку перетину$P'=\Pi'\cap (OP)$.

Загалом, перспективна проекція - це не біекція між площинами. Дійсно, якщо лінія$(OP)$ паралельна$\Pi'$ (тобто якщо$(OP)\cap\Pi'=\emptyset$), то перспективна$P\in \Pi$ проекція не визначена. Також, якщо$(OP')\parallel \Pi$ для$P'\in \Pi'$, то точка не$P'$ є зображенням перспективної проекції.

Наприклад,$O$ нехай є початком$(x,y,z)$ координатного простору і площин$\Pi$ і$\Pi'$ задаються рівняннями$z=1$ і$x=1$ відповідно. Тоді перспективна проекція від$\Pi$ до$\Pi'$ може бути записана в координатах як

$(x,y,1)\mapsto (1,\dfrac{y}{x},\dfrac{1}{x}).$

Дійсно, координати повинні бути пропорційними; точки на$\Pi$ мають одиницю$z$ -координату, а точки на$\Pi'$ мають одиницю$z$ -координату.

Перспективна проекція, відображає одну площину на іншу. Однак ми можемо ідентифікувати дві площини, закріпивши систему координат у кожній. У цьому випадку ми отримуємо частково визначену карту від літака до себе. Ми збережемо трансформацію перспективи назви для таких карт.

Для описаної проекції перспективи; ми можемо отримати карту

\[\beta\:(x,y)\mapsto (\dfrac{1}{x},\dfrac{y}{x}).\]

Ця карта не визначена на лінії$x=0$. Також точки на цій лінії не є зображеннями точок під перспективною проекцією.

$\hat \Pi'$Позначають$\hat \Pi$ і проективні завершення$\Pi$ і$\Pi'$ відповідно. Зауважте, що перспективна проекція є обмеженням композиції двох бієкцій,$\hat \Pi\leftrightarrow\Phi \leftrightarrow\hat \Pi'$ побудованих у попередньому розділі. За спостереженням 15.3.1 перспективна проекція може бути розширена до біекції,$\hat \Pi\leftrightarrow\hat \Pi'$ яка посилає лінії на лінії. (Аналогічна історія сталася і з інверсією. Інверсія не визначена в її центрі; крім того, центр не є зворотним будь-якій точці. Для вирішення цієї проблеми ми перейшли до зворотної площини, яка є евклідовою площиною, розширеною однією ідеальною точкою. Та ж стратегія працювала і для перспективної проекції$\Pi \to \Pi'$, але цього разу нам потрібно додати ідеальну лінію.)

Наприклад, щоб визначити розширення перспективної проекції$\beta$ в 15.4.1, ми повинні зауважити, що

Олівець вертикальних ліній$x=a$ наноситься на себе.
Ідеальні точки, визначені олівцем ліній,$y=m \cdot x+ b$ зіставляються з точкою,$(0,m)$ а навпаки — точка$(0, m)$ відображається на ідеальній точці, визначеній олівцем ліній$y=m \cdot x+ b$.