10.4: Спосіб інверсії

Last updated
Save as PDF

Page ID: 59092

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Ось додаток інверсії, яке ми включаємо як ілюстрацію; ми не будемо використовувати його далі в книзі.

Теорема$\PageIndex{1}$ Ptolemy's identity.

$ABCD$Дозволяти вписаний чотирикутник. Припустимо, що точки$A,B,C$, і$D$ з'являються на окружній лінії в тому ж порядку. Тоді

$AB \cdot CD + BC \cdot DA = AC \cdot BD.$

Доказ

Припустимо, що точки$A,B,C,D$ лежать на одній лінії в такому порядку.

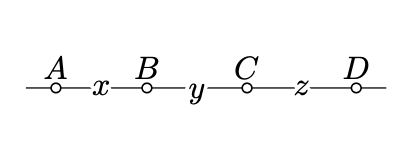
$2021-02-22 пнг$

Набір$x = AB$,$y = BC$,$z = CD$. Зверніть увагу, що

$x \cdot z + y \cdot (x + y + z) = (x + y) \cdot (y + z).$

Оскільки$AC = x + y$, і$BD = y + z$$DA = x + y + z$, це підтверджує особистість.

Залишається розглянути випадок, коли чотирикутник$ABCD$ вписаний в коло, скажімо$\Gamma$.

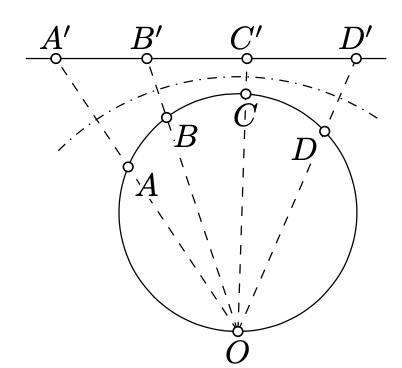
$2021-02-22 пнг$

Особистість може бути переписана як

$\dfrac{AB \cdot DC}{BD \cdot CA} + \dfrac{BC \cdot AD}{CA \cdot DB} = 1.$

На лівій стороні у нас є два перехресних співвідношення. Згідно з теоремою 10.3.1a, ліва сторона не змінюється, якщо застосувати інверсію до кожної точки.

Розглянемо інверсію в колі по центру в точці$O$, яка лежить$\Gamma$ між$A$ і$D$. За теоремою 10.3.2 ця інверсія$\Gamma$ відображає лінію. Це зводить проблему до того випадку$A, B, C$, коли і$D$ лежать на одній лінії, яка вже розглядалася.

У наведеному вище доказі ми переписуємо особистість Птолемея у формі, яка є інваріантною щодо інверсії, а потім застосовуємо інверсію, яка робить твердження очевидним. Рішення наступної вправи засноване на тій же ідеї; потрібно зробити правильний вибір інверсії.

Вправа$\PageIndex{1}$

Припустимо, що чотири кола взаємно дотичні один до одного. Покажіть, що чотири (серед шести) їх точок дотику лежать на одній лінії кола.

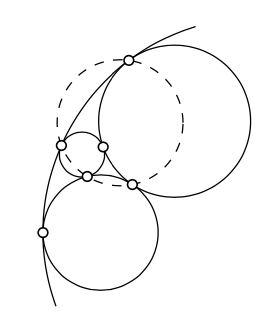
$2021-02-22 пнг$

Підказка

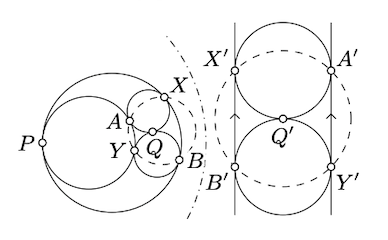
$2021-02-22 пнг$

Позначте точки дотику по$X, Y , A, B, P$, і$Q$ як на схемі. Нанесіть інверсію з центром в$P$. Зверніть увагу, що два кола, які дотичні в,$P$ стають паралельними лініями, а інші два кола дотичні один до одного і ці дві паралельні лінії.

Зверніть увагу, що точки дотику$A'$,$B'$$X'$, і$Y'$ з паралельними лініями є вершинами квадрата; зокрема вони лежать на одному колі. Ці точки є зображеннями$A, B, X$, і$Y$ під інверсією. За теоремою 10.3.1 точки$A, B, X$, а$Y$ також лежать на одній лінії кола.

Вправа$\PageIndex{2}$

Припустимо, що три кола дотичні один до одного і до двох паралельних ліній, як показано на малюнку.

Показати, що лінія, що проходить через$A$ і також$B$ є дотичною до двох кіл в$A$.

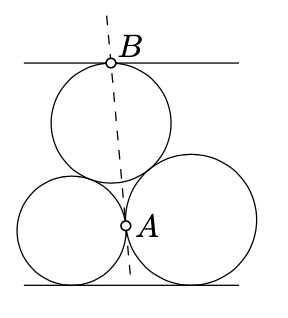
$2021-02-22 пнг$

Підказка

Нанесіть інверсію по колу з центром$A$. Точка$A$ піде до нескінченності, два кола дотичні в$A$ стануть паралельними лініями, а дві паралельні лінії стануть колами дотичними в$A$; див. Діаграму.

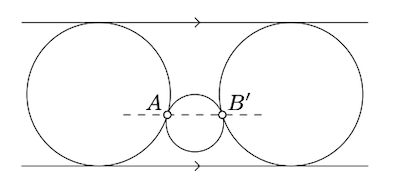
$2021-02-22 пнг$

Залишилося показати, що пунктирна лінія ($AB'$) паралельна іншим двом лініям.

Теорема\(\PageIndex{1}\) Ptolemy's identity.

Вправа\(\PageIndex{1}\)

Вправа\(\PageIndex{2}\)