9.6: Тангенсні напівлінії

Last updated
Save as PDF

Page ID: 59220

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Припустимо,$ABC$ це дуга кола$\Gamma$. Половина лінії$[AX)$ називається дотичною до дуги$ABC$,$A$ якщо лінія$(AX)$ дотична до$\Gamma$, а точки$X$ і$B$ лежать на одній стороні прямої$(AC)$.

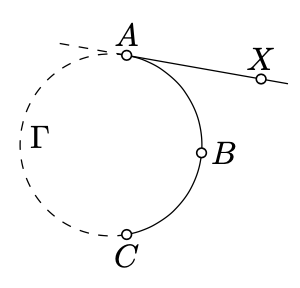
$2021-02-19 пнг$

Якщо дуга утворена відрізком лінії,$[AC]$ то половина лінії$[AC)$ вважається дотичною в$A$. Якщо дуга утворена об'єднанням двох половинок$[AX)$ і$[BY)$ в$(AC)$, то$[AX)$ полупряма вважається дотичною до дуги в$A$.

Пропозиція$\PageIndex{1}$

Половина лінії$[AX)$ дотична до дуги,$ABC$ якщо і тільки якщо

$\measuredangle ABC + \measuredangle CAX \equiv \pi$.

Доказ

Для виродженої$ABC$ дуги твердження очевидне. Далі припускаємо,$ABC$ що дуга невироджена.

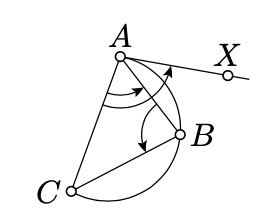
$2021-02-19 пнг$

Застосовуючи теорему 9.1.1 та теорему 9.2.1, отримаємо, що

$2 \cdot \measuredangle ABC + 2 \cdot \measuredangle CAX \equiv 0$.

Тому або

$\measuredangle ABC + \measuredangle CAX \equiv \pi$, або$\measuredangle ABC + \measuredangle CAX \equiv 0$.

Так як$[AX)$ є дотичною півлінії до дуги$ABC, X$ і$B$ лежать на одній стороні$(AC)$. За наслідками 3.4.1 і теореми 3.3.1, кути$CAX$$CAB$, і$ABC$ мають однаковий знак. Зокрема,$\measuredangle ABC + \measuredangle CAX \not\equiv 0$; тобто ми залишилися з справою

$\measuredangle ABC +\measuredangle CAX \equiv \pi$.

Вправа$\PageIndex{1}$

Показати, що існує унікальна дуга з кінцевими точками в заданих точках$A$ і$C$, що є дотичною до даної половини лінії$[AX)$ в$A$.

Підказка

Якщо$C \in (AX)$, то дуга - це відрізок лінії$[AC]$ або об'єднання двох напіврядків в$(AX)$ з вершинами в$A$ і$C$.

Припустимо$C \not\in (AX)$. $\ell$Дозволяти бути перпендикулярна лінія,$(AX)$ скинута від$A$ до і$m$ бути перпендикулярна бісектриса$[AC]$.

Зверніть увагу, що$\ell \nparallel m$; встановити$O = \ell \cap m$. Зверніть увагу, що коло з центром, що$O$$A$ проходить через, також проходить через$C$ і дотичною до$(AX)$.

Зверніть увагу, що одна дві дуги з кінцевими точками$A$ і$C$ є дотичною до$[AX)$.

Унікальність випливає з пропозиції$\PageIndex{1}$.

Вправа$\PageIndex{2}$

$[AX)$Дозволяти дотичній півлінії до дуги$ABC$. Припустимо,$Y$ це точка на дузі$ABC$, яка відрізняється від$A$. Покажіть, що$\measuredangle XAY \to 0$ як$AY \to 0$.

Підказка: Скористайтеся пропозицією$\PageIndex{1}$ та теоремою 7.4.1, щоб показати це$\measuredangle XAY = \measuredangle ACY$. За аксіомою IIiC,$\measuredangle ACY \to 0$ як$AY \to 0$; звідси і результат.

Вправа$\PageIndex{3}$

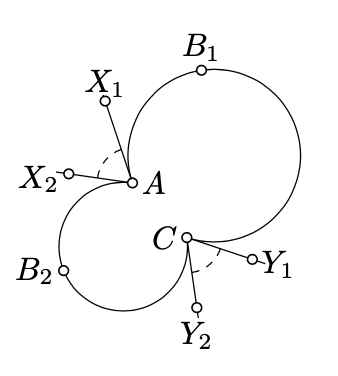
Дано дві дуги кола$AB_1C$ і$AB_2C$, нехай$[AX_1)$ і$[AX_2)$ в$A$,$[CY_1)$ і і$[CY_2)$ бути півлінії дотичними до дуг$AB_1C$ і$AB_2C$ в$C$. Покажіть, що

$\measuredangle X_1AX_2 \equiv -\measuredangle Y_1CY_2.$

$2021-02-19 пнг$

Підказка

Застосовуйте Пропозицію$\PageIndex{1}$ двічі.

(Крім того, застосуйте Слідство 5.4.1 для відображення через перпендикулярну бісектрису$[AC]$.)

Пропозиція\(\PageIndex{1}\)

Вправа\(\PageIndex{1}\)

Вправа\(\PageIndex{2}\)

Вправа\(\PageIndex{3}\)