9.5: Дуги окружностей

Last updated
Save as PDF

Page ID: 59221

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Підмножина кола, обмеженого двома точками, називається дугою кола.

Точніше, припустимо, що$A, B, C$ це різні точки на колі$\Gamma$. Дуга кола$ABC$ - це підмножина, яка включає точки, а$A, C$ також всі точки на$\Gamma$ цьому лежать з$B$ тієї ж сторони$(AC)$.

Для дуги$ABC$ кола точки$A$ і$C$ називаються кінцевими точками. Є точно дві окружні дуги$\Gamma$ з заданими кінцевими точками; вони протилежні один одному.

Припустимо$X$, буде ще один момент на$\Gamma$. За наслідком 9.3.2 ми маємо це$2 \cdot \measuredangle AXC \equiv 2 \cdot \measuredangle ABC$; тобто

$\measuredangle AXC \equiv \measuredangle ABC$або$\measuredangle AXC \equiv \measuredangle ABC + \pi.$

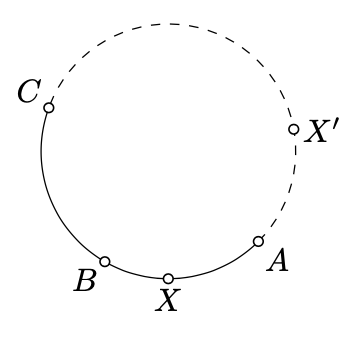
$2021-02-19 пнг$

Нагадаємо, що$X$ і$B$ лежати на одній стороні від$(AC)$ якщо і тільки якщо$\angle AXC$ і$\angle ABC$ мають однаковий знак (див. Вправу 3.4.2). Звідси випливає, що

$X$лежить на дузі$ABC$ тоді і тільки якщо

$\measuredangle AXC \equiv \measuredangle ABC$;

$X$лежить на дузі, протилежної$ABC$ якщо

$\measuredangle AXC \equiv \measuredangle ABC + \pi$.

Зверніть увагу, що дуга кола$ABC$ визначається, якщо$\triangle ABC$ вона не вироджена. Якщо$\triangle ABC$ вироджена, то дуга$ABC$ визначається як підмножина лінії, обмеженої$A$ і$C$ яка містить$B$.

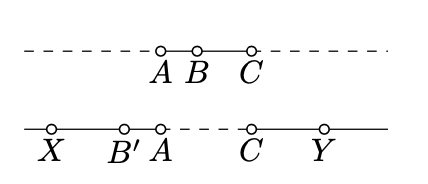
$2021-02-19 пнг$

Точніше, якщо$B$ лежить між$A$ і$C$, то дуга$ABC$ визначається як відрізок лінії$[AC]$. Якщо$B'$ лежить на продовженні$[AC]$, то дуга$AB'C$ визначається як об'єднання нероз'єднаних напівліній$[AX)$ і$[CY)$ в$(AC)$. При цьому дуги$ABC$ і$AB'C$ називаються навпроти один одного.

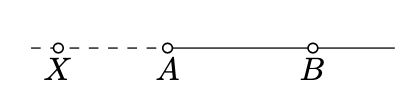
$2021-02-19 пнг$

Крім того, будь-яка напівлінія$[AB)$ буде розглядатися як дуга. Якщо$A$ лежить між$B$ і$X$, то$[AX)$ будуть називатися протилежними до$[AB)$. Ця вироджена дуга має лише одну кінцеву точку$A$.

Зручно буде використовувати поняття кругової лінії, що означає коло або лінія. Наприклад, будь-яка дуга є підмножиною окружної лінії; ми також можемо використовувати термін дуга кола, якщо хочемо підкреслити, що дуга може бути виродженою. Зверніть увагу, що для будь-яких трьох різних точок$A, B$$C$ існує і унікальна окружна дуга$ABC$.

Наступне твердження підсумовує обговорення вище.

Пропозиція$\PageIndex{1}$

$ABC$Дозволяти дуга кола і$X$ бути точкою, відмінною від$A$ і$C$. Тоді

(а)$X$ лежить на дузі$ABC$ тоді і тільки тоді, коли

$\measuredangle AXC = \measuredangle ABC;$

(б)$X$ лежить на дузі, протилежній$ABC$ якщо і тільки якщо

$\measuredangle AXC \equiv \measuredangle ABC + \pi$;

Вправа$\PageIndex{1}$

За заданим гострим трикутником$ABC$ зробіть компас-лінійку побудови точки$Z$ таким чином, що

$\measuredangle AZB = \measuredangle BZC = \measuredangle CZA = \pm \dfrac{2}{3} \cdot \pi$

Підказка

$2021-02-19 пл.$

Вгадайте конструкцію по схемі. Щоб показати, що вона виробляє необхідну точку, застосуйте теорему 9.2.1.

Вправа$\PageIndex{2}$

Припустимо, що точка$P$ лежить на окружності рівностороннього трикутника$ABC$ і$PA \le PB \le PC$. Покажіть, що$PA + PB = PC$.

Підказка

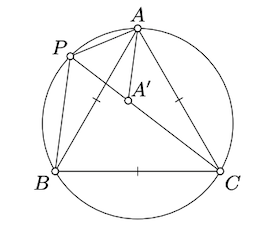
$2021-02-19 пнг$

Показати, що$P$ лежить на дузі протилежної від$ACB$; зробити висновок, що$\measuredangle APC = \measuredangle CPB = \pm \dfrac{\pi}{3}$.

Вибирайте точку$A' \in [PC]$ таку, що$PA' = PA$. Зверніть увагу, що$\triangle APA'$ є рівностороннім. Доведіть і використовуйте це$\triangle AA'C \cong \triangle APB.$

Чотирикутник$ABCD$ вписується, якщо всі точки$A, B, C$, і$D$ лежать на окружній лінії$\Gamma$. Якщо дуги$ABC$ і$ADC$ протилежні, то скажемо, що точки$A, B, C$, і$D$ з'являються далі$\Gamma$ в тому ж циклічному порядку.

Це визначення дає можливість сформулювати наступне уточнення Слідство 9.3.2, яке включає вироджені чотирикутники. Це випливає безпосередньо з Пропозиції$\PageIndex{1}$.

Пропозиція$\PageIndex{2}$

Чотирикутник$ABCD$ вписується в коло, якщо і тільки якщо

$\measuredangle ABC = \measuredangle ADC$або$\measuredangle ABC \equiv \measuredangle ADC + \pi.$

Більш того, друга ідентичність тримається тоді і тільки в тому випадку, якщо точки$A,B,C,D$ з'являються на окружній лінії в тому ж циклічному порядку.

Пропозиція\(\PageIndex{1}\)

Вправа\(\PageIndex{1}\)

Вправа\(\PageIndex{2}\)

Пропозиція\(\PageIndex{2}\)