9.2: Вписаний кут

Ми говоримо, що трикутник вписаний в коло,$\Gamma$ якщо всі його вершини лежать на$\Gamma$.

Теорема$\PageIndex{1}$

$\Gamma$Дозволяти бути коло з центром$O$, і$X, Y$ бути дві різні точки на$\Gamma$. Потім$\triangle XPY$ вписується в$\Gamma$ якщо і тільки якщо

$$2 \cdot \measuredangle XPY \equiv \measuredangle XOY.$$

Аналогічно, якщо і тільки якщо

$\measuredangle XPY \equiv \dfrac{1}{2} \cdot \measuredangle XOY$або$\measuredangle XPY \equiv \pi + \dfrac{1}{2} \cdot \measuredangle XOY.$

Доказ

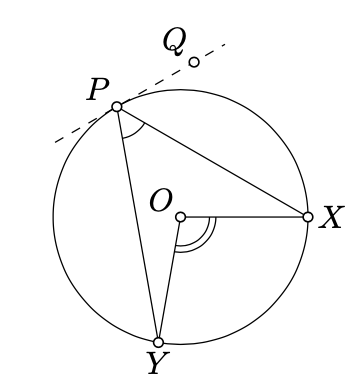
частина «тільки якщо». $(PQ)$Дозволяти бути дотичною лінією до$\Gamma$ at$P$. За теоремою 9.1.1

$2 \cdot \measuredangle QPX \equiv \measuredangle POX$,$2 \cdot \measuredangle QPY \equiv \measuredangle POY.$

Віднімаючи одну ідентичність з іншого, отримуємо 9.2.1.

Частина «Якщо». Припустимо, що 9.2.1 тримає для деяких$P \not\in \Gamma$. Зауважте, що$\measuredangle XOY \ne 0$. Отже,$\measuredangle XPY \ne 0$ ні$\pi$;$\measuredangle PXY$ тобто не вироджений.

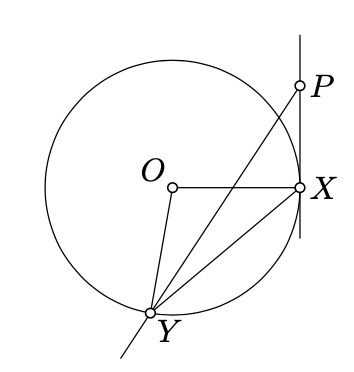
Лінія$(PX)$ може бути дотичною до точки$X$ або перетинатися$\Gamma$ в іншій$\Gamma$ точці; в останньому випадку припустимо, що$P'$ позначає цю точку перетину.

У першому випадку, за теоремою 9.1, ми маємо

$2 \cdot \measuredangle PXY \equiv \measuredangle XOY \equiv 2 \cdot \measuredangle XPY.$

Застосовуючи поперечну властивість (теорема 7.3.1), отримуємо те$(XY) \parallel (PY)$, що неможливо, оскільки$\triangle PXY$ є невиродженим.

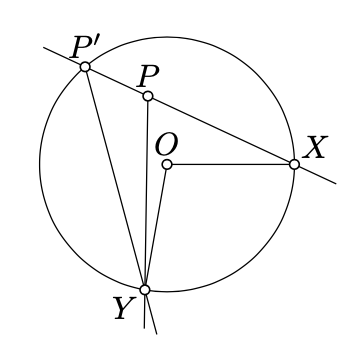
У другому випадку, застосовуючи частину «якщо» і те$P, X$, і$P'$ лягаємо на одну лінію (див. Вправа 2.4.2) отримуємо, що

$\begin{array} {rcl} {2 \cdot \measuredangle P'PY} & \equiv & {2 \cdot \measuredangle XPY \equiv \measuredangle XOY \equiv} \\ {} & \equiv & {2 \cdot \measuredangle XP'Y \equiv 2 \cdot \measuredangle XP'P.} \end{array}$

Знову ж таки, поперечним властивістю$(PY) \parallel (P'Y)$, яке неможливо, оскільки$\triangle PXY$ є невиродженим.

Вправа$\PageIndex{1}$

Дозволяти$X, X', Y$, і$Y'$ бути різні точки на колі$\Gamma$. Припустімо, що$(XX')$ зустрічається$(YY')$ в точці$P$. Покажіть, що

(а)$2 \cdot \measuredangle XPY \equiv \measuredangle XOY + \measuredangle X'OY'$;

(б)$\triangle PXY \sim \triangle PY'X'$;

(c)$PX \cdot PX' = |OP^2 - r^2|$, де$O$ знаходиться центр і$r$ радіус$\Gamma$.

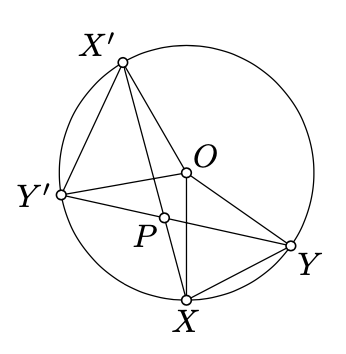
($OP^2 - r^2$Величиною називається сила точки$P$ по відношенню до кола$\Gamma$. Частина (c) вправи робить його корисним інструментом для вивчення кіл, але ми не збираємося розглядати його далі в книзі.)

Підказка

(а) Застосувати теорему$\PageIndex{1}$ для$\angle XX'Y$$\angle X'YY'$ та та теорему 7.4.1 для$\triangle PYX'$.

(b) Якщо$P$ знаходиться всередині$\Gamma$ то$P$ лежить між$X$ і між$X'$ і між$Y$ і$Y'$ в цьому випадку$\angle XPY$ вертикально до$\angle X'PY'$. Якщо$P$ знаходиться за межами$\Gamma$ то$[PX) = [PX')$ і$[PY) = [PY')$. В обох випадках ми маємо це$\measuredangle XPY = \measuredangle X'PY'$.

Застосовуючи теорему$\PageIndex{1}$ і вправу 2.4.2, ми отримуємо, що

$2 \cdot \measuredangle Y'X'P \equiv 2 \cdot \measuredangle Y'X'X \equiv 2 \cdot \measuredangle Y'YX \equiv 2 \dot \measuredangle PYX.$

Відповідно до теореми 3.3.1,$\angle Y'X'P$ і$\angle PYX$ мають однаковий знак; отже$\measuredangle Y'X'P = \measuredangle PYX$. Залишилося застосувати умову подібності АА.

(c) Застосувати (b)$[YY']$ припускаючи, що діаметр$\Gamma$.

Вправа$\PageIndex{2}$

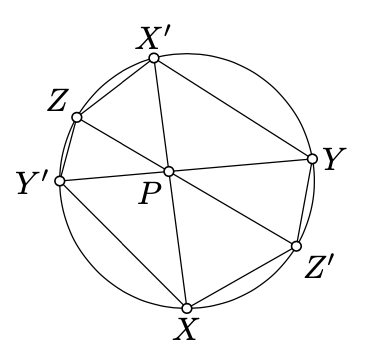
Три хорди$[XX']$$[YY']$, і$[ZZ']$ кола$\Gamma$ перетинаються в точці$P$. Покажіть, що

$XY' \cdot ZX' \cdot YZ' = X'Y \cdot Z'X \cdot Y'Z.$

Підказка

Застосовуйте вправу\ (\ pageIndex {1} b тричі.

Вправа$\PageIndex{3}$

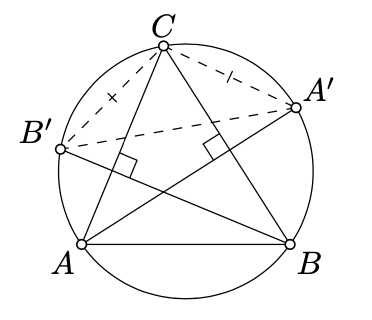
$\Gamma$Дозволяти бути окружністю гострого трикутника$ABC$. Нехай$A'$ і$B'$ позначають другі точки перетину висот від$A$ і$B$ с$\Gamma$. Покажіть,$\triangle A'B'C$ що рівнобедрений.

Підказка

$X$$Y$Дозволяти і бути точки підніжжя висот від$A$ і$B$. Припустимо, що$O$ позначає циркуцентр.

За умовою АА,$\triangle AXC \sim \triangle BYC$. Тоді

$\measuredangle A'OC \equiv 2 \cdot \measuredangle A'AC \equiv - 2 \cdot \measuredangle B'BC \equiv - \measuredangle B'OC.$

За SAS,$\triangle A'OC \cong \triangle B'OC$. Тому,$A'C = B'C$.

Вправа$\PageIndex{4}$

$[XY]$$[X'Y']$Дозволяти і бути двома паралельними акордами кола. Покажіть, що$XX' = YY'$.

Вправа$\PageIndex{5}$

Дивитися «Чому тут пі? І чому вона в квадраті? Геометрична відповідь на проблему Базеля» Гранта Сандерсона. (Він доступний на YouTube.)

Підготуйте одне питання.