6.4: Нерівність Птолемея

Last updated
Save as PDF

Page ID: 59002

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Чотирикутник визначається як впорядкований чотиримісний з різних точок на площині. Ці 4 точки називаються вершинами чотирикутника. Чотирикутник ABCD також буде позначатися символом$\square ABCD$.

Дано чотирикутник$ABCD$, чотири сегменти$[AB]$$[BC]$,$[CD]$,, і$[DA]$ називаються сторонами$\square ABCD$; інші два сегменти$[AC]$ і$[BD]$ називаються діагоналями$\square ABCD$.

Теорема$\PageIndex{1}$ Ptolemy's inequality

У будь-якому чотирикутнику добуток діагоналей не може перевищувати суму добутків його протилежних сторін; тобто

\[AC \cdot BD \le AB \cdot CD + BC \cdot DA\]

для будь-якого$\square ABCD$.

Наведемо класичне доказ цієї нерівності методом подібних трикутників з додатковою побудовою. Цей доказ наведено як ілюстрацію — він не буде використовуватися далі в продовженні.

Доказ

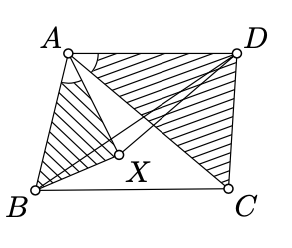
$2021-02-09 9.05.34 пнг$

Розглянемо полустрочку$[AX)$ таку, що$\measuredangle BAX = \measuredangle CAD$. У цьому випадку$\measuredangle XAD = \measuredangle BAC$ з додаванням$\measuredangle BAX$ або$\measuredangle CAD$ до відповідних сторін виходить$\measuredangle BAD$. Можна припустити, що

$AX = \dfrac{AB}{AC} \cdot AD.$

У цьому випадку ми маємо

$\dfrac{AX}{AD} = \dfrac{AB}{AC}$,$\dfrac{AX}{AB} = \dfrac{AD}{AC}.$

Звідси

$\triangle BAX \sim \triangle CAD$,$\triangle XAD \sim \triangle BAC$.

Тому,

$\dfrac{BX}{CD} = \dfrac{AB}{AC}$,$\dfrac{XD}{BC} = \dfrac{AD}{AC}.$

або, еквівалентно

$AC \cdot BX = AB \cdot CD$,$AC \cdot XD = BC \cdot AD$.

Додавши ці дві рівності, ми отримуємо

$AC \cdot (BX + XD) = AB \cdot CD + BC \cdot AD$.

Залишилося застосувати нерівність трикутника,$BD \le BX + XD$.

Використовуючи доказ вище разом із наслідком 9.3.2, можна показати, що рівність тримається лише у тому випадку, якщо вершини$A, B, C$, і$D$ з'являються на прямій або колі в тому ж циклічному порядку; див. також Теорему 10.4.1 для іншого доказу випадку рівності. Вправа 18.3.2 нижче пропонує ще один доказ нерівності Птолемея за допомогою складних координат.