6.2: Теорема Піфагора

Last updated
Save as PDF

Page ID: 58994

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Трикутник називається правим, якщо один з його кутів правильний. Сторона, протилежна прямому куту, називається гіпотенузою. Сторони, прилеглі до прямого кута, називаються ніжками.

Теорема$\PageIndex{1}$

Припустимо,$\triangle ABC$ це прямокутний трикутник з прямим кутом на$C$. Тоді

$AC^2 + BC^2 = AB^2.$

Доказ

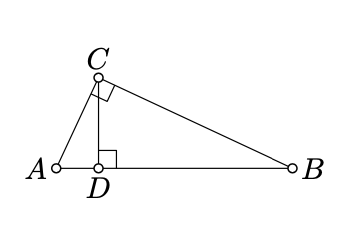
$2021-02-08 пнг$

$D$Дозволяти бути точкою стопи$C$ на$(AB)$.

Згідно з Леммою 5.5.1,

$AD < AC < AB$

$BD < BC < AB.$

Тому$D$ лежить між$A$ і$B$; зокрема,

\[AD + BD = AB.\]

Зверніть увагу, що за умовою подібності AA ми маємо

$\triangle ADC \sim \triangle ACB \sim \triangle CDB.$

Зокрема,

\[\dfrac{AD}{AC} = \dfrac{AC}{AB} \text{ and } \dfrac{BD}{BC} = \dfrac{BC}{BA}.\]

Давайте перепишемо дві ідентичності в 6.2.2:

$AC^2 = AB \cdot AD$і$BC^2 = AB \cdot BD$.

Підсумовуючи ці дві ідентичності та застосувавши 6.2.1, ми отримуємо, що

$AC^2 + BC^2 = AB \cdot (AD + BD) = AB^2.$

Вправа$\PageIndex{1}$

Припустимо$A, B, C$, і$D$ знаходяться як у доказі вище. Покажіть, що

$CD^2 = AD \cdot BD.$

Наступна вправа - зворотне до теореми Піфагора.

Підказка: Застосуйте це$\triangle ADC \sim \triangle CDB$.

Вправа$\PageIndex{2}$

Припустимо, що$ABC$ це трикутник такий, що

$AC^2 + BC^2 = AB^2.$

Доведіть, що кут під$C$ правильним.

Підказка: Застосувати теорему Піфагора$\PageIndex{1}$ та умову конгруентності ССС

Теорема\(\PageIndex{1}\)

Вправа\(\PageIndex{1}\)

Вправа\(\PageIndex{2}\)