Skip to main content
LibreTexts - Ukrayinska

24.4: Обсяг призм

  1. Last updated
  2. Save as PDF
  • Page ID
    900

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Урок

    Давайте розглянемо обсяг призм, які мають дробові вимірювання.

    Вправа\(\PageIndex{1}\): A Box of Cubes

    1. Скільки кубиків з довжиною краю в\(1\) дюйм заповнюють цю коробку?
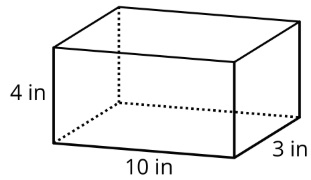
    clipboard_e9bb0cb3f1bb2ba90a25a92bead047869.png
    Малюнок\(\PageIndex{1}\)
    1. Якби кубики мали довжину краю\(2\) дюймів, вам потрібно було б більше чи менше кубиків, щоб заповнити коробку? Поясніть свої міркування.
    2. Якби кубики мали довжину краю в\(\frac{1}{2}\) дюйм, вам потрібно було б більше чи менше кубиків, щоб заповнити коробку? Поясніть свої міркування.

    Вправа\(\PageIndex{2}\): Cubes with Fractional Edge Lengths

    1. Дієго каже, що 108 кубів з довжиною краю в\(\frac{1}{3}\) дюйм потрібні для заповнення прямокутної призми, яка становить 3 дюйми на 1 дюйм на\(1\frac{1}{3}\) дюйм.
      1. Поясніть або покажіть, як це правда. Якщо ви застрягли, подумайте про складання схеми.
      2. Який об'єм прямокутної призми в кубічних дюймах? Поясніть або покажіть свої міркування.
    2. Лін і Ной упаковують маленькі кубики в більший куб з довжиною краю в\(1\frac{1}{2}\) дюйми. Лін використовує кубики з довжиною краю в\(\frac{1}{2}\) дюйм, а Ной використовує кубики з довжиною краю в\(\frac{1}{4}\) дюйм.
      1. Кому знадобиться більше кубиків, щоб заповнити\(1\frac{1}{2}\) дюймовий куб? Будьте готові пояснити свої міркування.
      2. Якщо Лін і Ной використовують свої маленькі кубики, щоб знайти об'єм більшого\(1\frac{1}{2}\) -дюймового куба, чи отримають вони однакову відповідь? Поясніть або покажіть свої міркування.

    Вправа\(\PageIndex{3}\): Fish Tank and Baking Pan

    1. Природний центр має акваріум у формі прямокутної призми. Танк довжиною\(10\) ноги,\(8\frac{1}{4}\) ноги в ширину і\(6\) ноги у висоту.
    1. Який обсяг бака в кубічних футах? Поясніть або покажіть свої міркування.
    clipboard_e16542e806afa256db70917b9d035ed30.png
    Ілюстрація\(\PageIndex{2}\): Акваріум рецифаль, Серж Талфер (Self-photed). Громадське надбання. Вікісховище. Джерело.
    1. Доглядач природного центру\(\frac{4}{5}\) заповнив резервуар водою. Яким був обсяг води в резервуарі, в кубічних футах? Якою була висота води в баку? Поясніть або покажіть свої міркування.
    2. Ще один день резервуар був заповнений 330 кубічних футів води. Висота води становила яку частку висоти бака? Покажіть свої міркування.
    1. Рецепт Клер для бананового хліба не впишеться в її улюблену каструлю. Пан\(8\frac{1}{2}\) дюймів на 11 дюймів на 2 дюйми. Тісто заповнює деко до самого верху, а при випіканні тісто розливається по боках. Щоб уникнути розливів, між верхньою частиною тесту і обідком каструлі має бути близько дюйма.
      Клер має ще одну каструлю, яка становить 9 дюймів на 9 дюймів на\(2\frac{1}{2}\) дюйми. Якщо вона використовує цю сковороду, чи буде тісто розливатися під час випікання?

    Ви готові до більшого?

    1. Знайти площу прямокутника з довжиною сторін\(\frac{1}{2}\) і\(\frac{2}{3}\).
    2. Знайти обсяг прямокутної призми з довжиною сторін\(\frac{1}{2}\)\(\frac{2}{3}\), і\(\frac{3}{4}\).
    3. Як ви думаєте, що станеться, якщо ми продовжуємо множити дроби\(\frac{1}{2}\cdot\frac{2}{3}\cdot\frac{3}{4}\cdot\frac{4}{5}\cdot\frac{5}{6}\ldots\)?
    4. Знайти площу прямокутника з довжиною сторін\(\frac{1}{1}\) і\(\frac{2}{1}\).
    5. Знайти обсяг прямокутної призми з довжиною сторін\(\frac{1}{1}\)\(\frac{2}{1}\), і\(\frac{1}{3}\).
    6. Як ви думаєте, що станеться, якщо ми продовжуємо множити дроби\(\frac{1}{1}\cdot\frac{2}{1}\cdot\frac{1}{3}\cdot\frac{4}{1}\cdot\frac{1}{5}\ldots\)?

    Резюме

    Якщо прямокутна призма має довжини країв\(a\)\(b\) одиниць,\(c\) одиниць і одиниць, об'єм є добутком\(a\)\(b\), і\(c\). \(V=a\cdot b\cdot c\)

    Це означає, що якщо ми знаємо обсяг і дві довжини краю, ми можемо розділити, щоб знайти довжину третього краю.

    Припустимо, обсяг прямокутної призми дорівнює 3\(400\frac{1}{2}\) см, довжина одного краю -\(\frac{11}{2}\) см, інший -\(6\) см, а довжина третього краю невідома. Ми можемо написати рівняння множення, щоб представити ситуацію:\(\frac{11}{2}\cdot 6\cdot ?=400\frac{1}{2}\)

    Третю довжину краю ми можемо знайти, розділивши:\(400\frac{1}{2}\div\left(\frac{11}{2}\cdot 6\right)=?\)

    Практика

    Вправа\(\PageIndex{4}\)

    Басейн у формі прямокутної призми наповнюється водою. Довжина і ширина басейну становить 24 футів і 15 футів. Якщо висота води в басейні становить\(1\frac{1}{3}\) фути, який обсяг води в кубічних футах?

    Вправа\(\PageIndex{5}\)

    Прямокутна призма вимірює\(2\frac{2}{5}\) дюйми на\(3\frac{1}{5}\) дюйми на 2 дюйми.

    1. Прия сказав: «Потрібно більше кубиків з довжиною краю\(\frac{2}{5}\) дюйм, ніж кубики з довжиною краю\(\frac{1}{5}\) дюйм, щоб упакувати призму». Чи згодні ви з Priya? Поясніть або покажіть свої міркування.
    2. Скільки кубиків з довжиною краю в\(\frac{1}{5}\) дюйм вміщається в призму? Покажіть свої міркування.
    3. Поясніть, як ви можете використовувати свою відповідь в попередньому питанні, щоб знайти об'єм призми в кубічних дюймах.

    Вправа\(\PageIndex{6}\)

    1. Ось прямокутний трикутник. Яка його площа?
    2. Яка висота\(h\) для основи, яка є\(\frac{5}{4}\) одиницями довжини? Покажіть свої міркування.
    clipboard_e157e734e886688284a3b6a6570af2e8b.png
    Малюнок\(\PageIndex{3}\): Прямокутний трикутник з горизонтальною основою внизу, позначений п'ятьма четвертими сантиметром. Одна сторона позначена трьома четвертими сантиметром, а інша сторона маркується 1 сантиметром. Від прямого кута до горизонтальної основи проводиться вертикальна пунктирна лінія і маркується h.

    (Від блоку 4.4.3)

    Вправа\(\PageIndex{7}\)

    Щоб дати своїм тваринам необхідні мінерали та поживні речовини, фермери та ранчо часто мають блок солі, який називається «сольовий лизати» - доступний для їх тварин, щоб лизати.

    1. Ранчер замовляє коробку сольовиків у формі кубика. Довжини країв кожного соляного лизунка -\(\frac{5}{12}\) стопа. Обсяг однієї сольової лизунки більше або менше 1 кубічного фута? Поясніть свої міркування.
    clipboard_eba9a5061870640c4b346f1bd6edbbf6e.png
    Малюнок\(\PageIndex{4}\): Сіль лизати 4 Beentree, Beentree (Власна робота). КУБ.СМ ПО-СА 4.0. Вікісховище. Джерело.
    1. Коробка, яка містить сіль лизати, - це\(1\frac{1}{4}\)\(1\frac{2}{3}\) ноги за\(\frac{5}{6}\) ногами. Скільки кубиків солі лизати поміститься в коробці? Поясніть або покажіть свої міркування.

    Вправа\(\PageIndex{8}\)

    1. Скільки груп\(\frac{1}{3}\) дюймів в\(\frac{3}{4}\) дюймах?
    2. Скільки дюймів у\(1\frac{2}{5}\) групах\(1\frac{2}{3}\) дюймів?

    (З блоку 4.4.1)

    Вправа\(\PageIndex{9}\)

    Ось таблиця, в якій показано співвідношення борошна і води в художній пасті. Заповніть таблицю значеннями в еквівалентних співвідношеннях.

    склянки борошна чашки води
    \(1\) \(\frac{1}{2}\)
    \(4\)
    \(3\)
    \(\frac{1}{2}\)
    Таблиця\(\PageIndex{1}\)

    (Від блоку 2.4.2)