Skip to main content
LibreTexts - Ukrayinska

24.2: Прямокутники з дробовими довжинами сторін

  1. Last updated
  2. Save as PDF
  • Page ID
    897

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Урок

    Давайте вивчимо прямокутники, які мають дробові вимірювання.

    Вправа\(\PageIndex{1}\): Areas of Squares

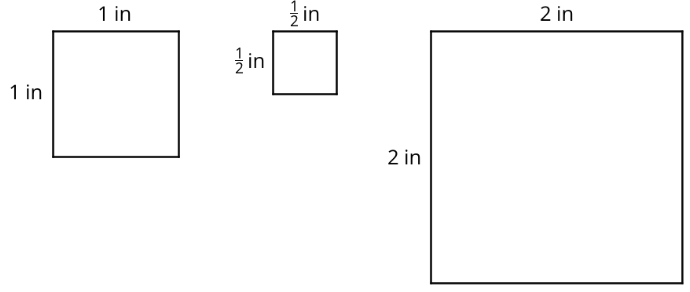
    clipboard_e311d490e1a167c5edb04509eb186d285.png
    Малюнок\(\PageIndex{1}\)
    1. Що ви помічаєте щодо площ площ?
    2. Кіран каже: «Квадрат з довжиною сторін\(\frac{1}{3}\) дюйма має площу\(\frac{1}{3}\) квадратних дюймів». Ви згодні? Поясніть або покажіть свої міркування.

    Вправа\(\PageIndex{2}\): Areas of Squares and Rectangles

    Ваш учитель дасть вам графічний папір і лінійку.

    1. На графічному папері намалюйте квадрат з довжиною сторін 1 дюйм. Усередині цього квадрата намалюйте ще один квадрат з довжиною сторін\(\frac{1}{4}\) дюйма.
      Використовуйте свій малюнок, щоб відповісти на питання.
      1. Скільки квадратів з довжиною сторін\(\frac{1}{4}\) дюйма може поміститися в квадраті з довжиною сторін 1 дюйм?
      2. Яка площа квадрата з довжиною сторін\(\frac{1}{4}\) дюйм? Поясніть або покажіть свої міркування.
    2. На графічному папері намалюйте прямокутник, який дорівнює\(3\frac{1}{2}\) дюймам на\(2\frac{1}{4}\) дюйми.
      Для кожного питання напишіть вираз поділу, а потім знайдіть відповідь.
      1. Скільки\(\frac{1}{4}\) -дюймових сегментів в довжину\(3\frac{1}{2}\) дюймів?
      2. Скільки\(\frac{1}{4}\) -дюймових сегментів в довжину\(2\frac{1}{4}\) дюймів?
    3. Використовуйте свій малюнок, щоб показати, що прямокутник, який\(3\frac{1}{2}\) дюйми на\(2\frac{1}{4}\) дюйми має площу\(7\frac{7}{8}\) квадратних дюймів.

    Вправа\(\PageIndex{3}\): Areas of Rectangles

    Кожен з цих виразів множення представляє площу прямокутника.

    \(2\cdot 4\qquad 2\frac{1}{2}\cdot 4\qquad 2\cdot 4\frac{3}{4}\qquad 2\frac{1}{2}\cdot 4\frac{3}{4}\)

    1. Всі області, затінені світло-блакитним кольором, мають однакову площу. Зіставте кожну діаграму з виразом, який, на вашу думку, представляє її область. Будьте готові пояснити свої міркування.
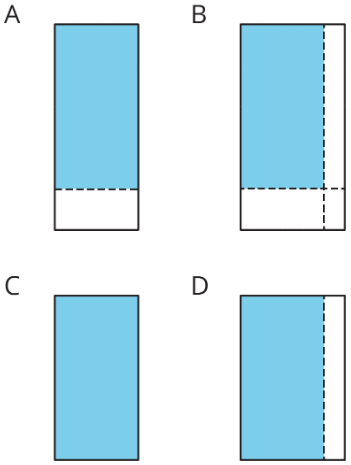
    clipboard_ee62b70a3993b2e8f07ba77076d2fcccd.png
    Малюнок\(\PageIndex{2}\): Чотири вертикально орієнтовані прямокутники, позначені A, B, C, D. Прямокутник A має горизонтальну пунктирну лінію приблизно на три чверті шляху вниз по ширині. Верхню частину відтіняють синім кольором. Прямокутник B має горизонтальну пунктирну лінію приблизно на три чверті шляху вниз по ширині і вертикальну пунктирну лінію приблизно на три чверті шляху праворуч від його довжини. Верхня ліва частина прямокутника затінена синім кольором. Прямокутник C затінений синім кольором. Прямокутник D має вертикальну пунктирну лінію приблизно на три чверті шляху праворуч від його довжини. Ліву частину прямокутника затінюємо синім кольором.
    1. Використовуйте діаграму, яка відповідає,\(2\frac{1}{2}\cdot 4\frac{3}{4}\) щоб показати, що значення\(2\frac{1}{2}\cdot 4\frac{3}{4}\) є\(11\frac{7}{8}\).

    Ви готові до більшого?

    Наступні прямокутники складаються з квадратів, і кожен прямокутник будується за допомогою попереднього прямокутника. Довжина сторони першого квадрата дорівнює 1 одиниці.

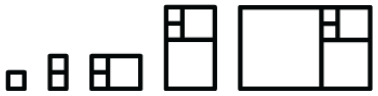
    clipboard_eb90b2b15c763a700e47a3a89e94b0a15.png
    Малюнок\(\PageIndex{3}\): Послідовність прямокутників, що складаються з квадратів. Перший - це одиниця квадрата. Другий складається з двох одиничних квадратів, укладаються вертикально. Третій складається з двох квадратів, складених вертикально, і 2 на 2 одиниці квадрата праворуч. Четвертий складається з двох одиниць квадратів, складені вертикально, 2 на 2 одиниці квадрат праворуч і 3 на 3 одиниці квадрат внизу. П'ятий складається з двох одиниць квадратів, складені вертикально, 2 на 2 одиниці квадрат праворуч, квадрат 3 на 3 одиниці в нижній частині, і 4 на 4 одиниці квадрат зліва.
    1. Намалюйте наступні чотири прямокутника, які побудовані таким же чином. Потім заповніть таблицю довжиною сторін прямокутника і часткою довшої сторони над коротшою стороною.
      коротка сторона довга сторона \(\frac{\text{long side}}{\text{short side}}\)
      \(1\) \ (\ frac {\ text {довга сторона}} {\ text {коротка сторона}}\) ">
      \(1\) \ (\ frac {\ text {довга сторона}} {\ text {коротка сторона}}\) ">
      \(2\) \ (\ frac {\ text {довга сторона}} {\ text {коротка сторона}}\) ">
      \(3\) \ (\ frac {\ text {довга сторона}} {\ text {коротка сторона}}\) ">
      \ (\ frac {\ text {довга сторона}} {\ text {коротка сторона}}\) ">
      \ (\ frac {\ text {довга сторона}} {\ text {коротка сторона}}\) ">
      \ (\ frac {\ text {довга сторона}} {\ text {коротка сторона}}\) ">
      \ (\ frac {\ text {довга сторона}} {\ text {коротка сторона}}\) ">
      \ (\ frac {\ text {довга сторона}} {\ text {коротка сторона}}\) ">
      Таблиця\(\PageIndex{1}\)
    2. Опишіть значення дробу довшої сторони над коротшою стороною. Що відбувається з фракцією, коли шаблон триває?

    Вправа\(\PageIndex{4}\): How Many Would it Take? (Part 2)

    Ной хотів би покрити прямокутний лоток прямокутною плиткою. Лоток має ширину\(11\frac{1}{4}\) дюймів і площу\(50\frac{5}{8}\) квадратних дюймів.

    1. Знайдіть довжину лотка в дюймах.
    2. Якщо плитка\(\frac{3}{4}\) дюйм за\(\frac{9}{16}\) дюймом, скільки потрібно Ною, щоб покрити лоток повністю, без зазорів або перекриттів? Поясніть або покажіть свої міркування.
    3. Намалюйте схему, щоб показати, як Ной міг укласти плитки. Ваша схема повинна показувати, скільки плиток знадобиться для покриття довжини і ширини лотка, але не потрібно показувати кожну плитку.

    Резюме

    Якщо прямокутник має довжини сторін\(a\) одиниці та\(b\) одиниці, площа є\(a\cdot b\) квадратними одиницями. Наприклад, якщо у нас є прямокутник з довжиною сторін\(\frac{1}{2}\) -дюйм, його площа становить\(\frac{1}{2}\cdot\frac{1}{2}\) або\(\frac{1}{4}\) квадратні дюйми.

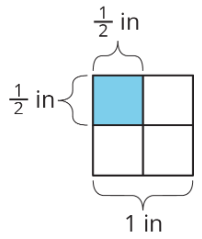
    clipboard_ef131bb7b81c480aa9e8b71b31ad4bd02.png
    Малюнок\(\PageIndex{4}\): Великий квадрат рівномірно розділений на 4 менших квадрата. Великий квадрат має довжину нижньої горизонтальної сторони 1 дюйм. З чотирьох менших квадратів верхній лівий квадрат затінений синім кольором. Він має довжину сторін, позначені половиною дюйма.

    Це означає, що якщо ми знаємо площу та довжину однієї сторони прямокутника, ми можемо розділити, щоб знайти довжину іншої сторони.

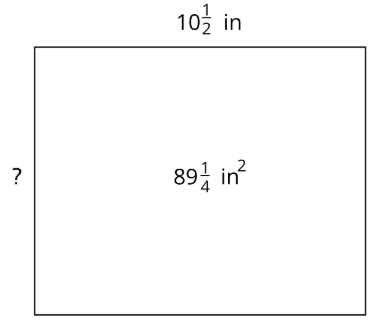
    clipboard_e0c229650bc2ccde698923d87b986f627.png
    Малюнок\(\PageIndex{5}\)

    Якщо довжина однієї сторони прямокутника знаходиться\(10\frac{1}{2}\) в, а його площа -\(89\frac{1}{4}\) у 2, ми можемо написати це рівняння, щоб показати їх зв'язок:\(10\frac{1}{2}\cdot ?=89\frac{1}{4}\)

    Потім ми можемо знайти довжину іншої сторони, в дюймах, використовуючи поділ:\(89\frac{1}{4}\div 10\frac{1}{2}=?\)

    Практика

    Вправа\(\PageIndex{5}\)

    1. Знайдіть невідому довжину сторони прямокутника, якщо його площа дорівнює 11 м 2. Покажіть свої міркування.
    clipboard_e784c05d2b238c257e3b9e949f072b0b9.png
    Малюнок\(\PageIndex{6}\): Прямокутник, який має площу з позначкою 11 метрів у квадраті. Довжина сторони однієї сторони прямокутника позначена трьома і двома третинами метрів, а довжина сторони іншої сторони позначена знаком питання. Кожен кут має вказаний символ прямого кута.
    1. Перевірте свою відповідь, помноживши її на задану довжину сторони (\(3\frac{2}{3}\)). Отриманий продукт 11? Якщо ні, перегляньте попередню роботу.

    Вправа\(\PageIndex{6}\)

    Працівник плиткою підлогу прямокутної кімнати, яка становить 12 футів на 15 футів. Плитки квадратні з довжиною сторін\(1\frac{1}{3}\) ноги. Скільки потрібно плитки, щоб покрити всю підлогу? Покажіть свої міркування.

    Вправа\(\PageIndex{7}\)

    Телевізійний екран має довжину\(16\frac{1}{2}\) дюймів, ширину\(w\) дюймів і площу\(462\) квадратних дюймів. Виберіть всі рівняння, які представляють співвідношення довжин сторін і площі телевізора.

    1. \(w\cdot 462=16\frac{1}{2}\)
    2. \(16\frac{1}{2}\cdot w=462\)
    3. \(462\div 16\frac{1}{2}=w\)
    4. \(462\div w=16\frac{1}{2}\)
    5. \(16\frac{1}{2}\cdot 462=w\)

    Вправа\(\PageIndex{8}\)

    Площа прямокутника знаходиться\(17\frac{1}{2}\) в 2, а його коротша сторона знаходиться\(3\frac{1}{2}\) в. Намалюйте схему, яка показує цю інформацію. Яка довжина довшої сторони?

    Вправа\(\PageIndex{9}\)

    Книжкова полиця довжиною 42 дюйми.

    1. Скільки книг довжиною\(1\frac{1}{2}\) дюймів поміститься на книжковій полиці? Поясніть свої міркування.
    2. Книжкова шафа має 5 таких книжкових полиць. Скільки футів місця на полицях? Поясніть свої міркування.

    (З блоку 4.4.1)

    Вправа\(\PageIndex{10}\)

    Знайдіть значення\(\frac{5}{32}\div\frac{25}{4}\). Покажіть свої міркування.

    (Від блоку 4.3.2)

    Вправа\(\PageIndex{11}\)

    Скільки груп\(1\frac{2}{3}\) знаходяться в кожній з цих величин?

    1. \(1\frac{5}{6}\)
    2. \(4\frac{1}{3}\)
    3. \(\frac{5}{6}\)

    (З блоку 4.2.3)

    Вправа\(\PageIndex{12}\)

    Потрібно\(1\frac{1}{4}\) кілька хвилин, щоб заповнити 3-літрове відро води за допомогою шланга. З цією швидкістю, скільки часу потрібно, щоб заповнити 50-галонну ванну? Якщо ви застрягли, подумайте про використання таблиці.

    (Від блоку 2.4.4)