Skip to main content
LibreTexts - Ukrayinska

24.3: Дробові довжини в трикутниках і призмах

  1. Last updated
  2. Save as PDF
  • Page ID
    896

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Урок

    Давайте вивчимо площу та об'єм, коли задіяні фракції.

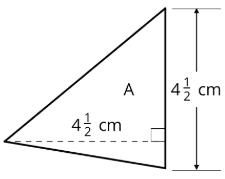
    Вправа\(\PageIndex{1}\): Area of Triangle

    Знайдіть площу трикутника A в квадратних сантиметрах. Покажіть свої міркування.

    clipboard_ec4fd5cf99a80835528317a18a248115c.png
    Малюнок\(\PageIndex{1}\): Трикутник з позначкою A з вертикальною стороною. Одна вершина знаходиться зліва від вертикальної сторони. Від першої вершини до вертикальної сторони трикутника проводиться пунктирна горизонтальна лінія і вказується символ прямого кута. штриховою лінією і вертикальною стороною обозначені як 4, так і на півтора сантиметри.

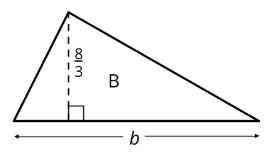
    Вправа\(\PageIndex{2}\): Bases and Heights of Triangles

    1. Площа трикутника B -\(8\) квадратні одиниці. Знайти довжину\(b\). Покажіть свої міркування.
    clipboard_e0c0141e7b8849498af7747ed4fb9cb9e.png
    Малюнок\(\PageIndex{2}\): Трикутник з позначкою B має горизонтальну сторону внизу трикутника і вершину над горизонтальною стороною. Від вершини до горизонтальної сторони проводиться пунктирна лінія і вказується символ прямого кута. Горизонтальна сторона позначається малим літером b, а пунктирною лінією позначається вісім третин.
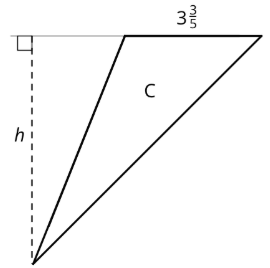
    1. Площа трикутника С -\(\frac{54}{5}\) квадратні одиниці. Яка довжина\(h\)? Покажіть свої міркування.
    clipboard_ead3b041e5590603b08bba55b2a5fe215.png
    Рисунок\(\PageIndex{3}\): Трикутник з позначкою C має горизонтальну сторону у верхній частині трикутника і вершину нижче горизонтальної сторони і ліворуч. З горизонтальної сторони і вліво проходить горизонтальна лінія. Від нижньої вершини до розширеної горизонтальної лінії проводиться вертикальна пунктирна лінія і вказується символ прямого кута. штриховою лінією позначається h і горизонтальна сторона трикутника маркується 3 і три п'яті.

    Вправа\(\PageIndex{3}\): Volumes of Cubes and Prisms

    Використовуйте кубики або аплет, щоб допомогти вам відповісти на наступні запитання.

    1. Ось креслення куба з довжиною країв 1 дюйм.
      1. Скільки кубів з довжиною країв\(\frac{1}{2}\) дюймів потрібно для заповнення цього куба?
      2. Який об'єм у кубічних дюймах куба з довжиною країв\(\frac{1}{2}\) дюймів? Поясніть або покажіть свої міркування.
    clipboard_e4906f09d14737e9b2ad156d4fe14c74c.png
    Малюнок\(\PageIndex{4}\)
    1. Чотири кубика складають в одну стопку, щоб вийшла призма. Кожен куб має довжину краю в\(\frac{2}{2}\) дюйм. Намалюйте призму, і знайдіть її обсяг в кубічних дюймах.
    2. Використовуйте кубики з довжиною краю\(\frac{1}{2}\) дюйм, щоб побудувати призми з довжиною, шириною та висотою, показаними в таблиці.
      1. Для кожної призми запишіть в таблиці, скільки\(\frac{1}{2}\) -дюймових кубиків можна упакувати в призму і обсяг призми.
        довжина призми (в) ширина призми (дюйми) висота призми (в) кількість\(\frac{1}{2}\) -дюймових кубів у призмі об'єм призми (в 3)
        \(\frac{1}{2}\) \(\frac{1}{2}\) \(\frac{1}{2}\) \ (\ frac {1} {2}\) -дюймові кубики в призмі">
        \(1\) \(1\) \(\frac{1}{2}\) \ (\ frac {1} {2}\) -дюймові кубики в призмі">
        \(2\) \(1\) \(\frac{1}{2}\) \ (\ frac {1} {2}\) -дюймові кубики в призмі">
        \(2\) \(2\) \(1\) \ (\ frac {1} {2}\) -дюймові кубики в призмі">
        \(4\) \(2\) \(\frac{3}{2}\) \ (\ frac {1} {2}\) -дюймові кубики в призмі">
        \(5\) \(4\) \(2\) \ (\ frac {1} {2}\) -дюймові кубики в призмі">
        \(5\) \(4\) \(2\frac{1}{2}\) \ (\ frac {1} {2}\) -дюймові кубики в призмі">
        Таблиця\(\PageIndex{1}\)
      2. Вивчіть значення в таблиці. Що ви помічаєте про взаємозв'язок між довжинами країв кожної призми і її об'ємом?
    3. Який обсяг прямокутної призми, тобто\(1\frac{1}{2}\) дюйми на\(2\frac{1}{4}\) дюйми на\(4\) дюйми? Покажіть свої міркування.

    Ви готові до більшого?

    Одиничний дріб має a\(1\) в чисельнику.

    • Це одиничні фракції:\(\frac{1}{3}, \frac{1}{100}, \frac{1}{1}\).
    • Це не одиничні фракції:\(\frac{2}{9},\frac{8}{1}, 2\frac{1}{5}\).
    1. Знайдіть три одиничні дроби, сума яких дорівнює\(\frac{1}{2}\). Прикладом є:\(\frac{1}{8}+\frac{1}{8}+\frac{1}{4}=\frac{1}{2}\) Скільки подібних прикладів ви можете знайти?
    2. Знайдіть коробку, площа поверхні якої в квадратних одиницях дорівнює її об'єму в кубічних одиницях. Скільки подібного ви можете знайти?

    Резюме

    Якщо прямокутна призма має довжину країв 2 одиниці, 3 одиниці та 5 одиниць, ми можемо думати про неї як про 2 шари одиничних кубів, причому кожен шар має\((3\cdot 5)\) одиничні кубики в ньому. Отже, обсяг, в кубічних одиницях, становить:\(2\cdot 3\cdot 5\)

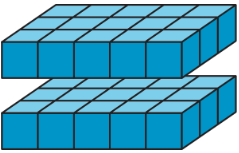
    clipboard_e6c8bf03d532e96a17ed6e571e061660a.png
    Малюнок\(\PageIndex{5}\)

    Щоб знайти об'єм прямокутної призми з дробовими довжинами ребер, ми можемо вважати її побудованою з кубів, які мають одиничну частку для їх довжини краю. Наприклад, якщо ми побудуємо призму, яка\(\frac{1}{2}\) -дюйм заввишки,\(\frac{3}{2}\) -дюйм шириною і 4 дюйми довжиною, використовуючи кубики з довжиною краю\(\frac{1}{2}\) -дюйм, ми б мали:

    • Висота в 1 куб, тому що\(1\cdot\frac{1}{2}=\frac{1}{2}\).
    • Ширина 3 кубика, тому що\(3\cdot\frac{1}{2}=\frac{3}{2}\).
    • Довжина 8 кубиків, тому що\(8\cdot\frac{1}{2}=4\).

    Обсяг призми буде дорівнює\(1\cdot 3\cdot 8\), або 24 кубічних одиниці. Як ми знаходимо його обсяг в кубічних дюймах? Ми знаємо, що кожен куб з довжиною краю\(\frac{1}{2}\) -дюйм має обсяг\(\frac{1}{8}\) кубічного дюйма, тому що\(\frac{1}{2}\cdot\frac{1}{2}\cdot\frac{1}{2}=\frac{1}{8}\). Оскільки призма побудована з використанням\(24\) цих кубів, її обсяг, у кубічних дюймах, тоді буде\(24\cdot\frac{1}{8}\), або\(3\) кубічні дюйми.

    Обсяг призми, в кубічних дюймах, також можна знайти, помноживши дробові довжини ребер в дюймах:\(\frac{1}{2}\cdot\frac{3}{2}\cdot 4=3\)

    Практика

    Вправа\(\PageIndex{4}\)

    Клер використовує маленькі дерев'яні кубики з довжиною краю\(\frac{1}{2}\) дюйм, щоб побудувати більший куб, який має довжину краю 4 дюйми. Скільки маленьких кубиків їй потрібно? Поясніть свої міркування.

    Вправа\(\PageIndex{5}\)

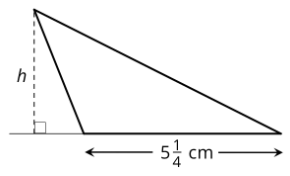
    Трикутник має площу 2\(7\frac{7}{8}\) см і підставу\(5\frac{1}{4}\) см.

    Яка довжина\(h\)? Поясніть свої міркування.

    clipboard_ed3b914d6b50be8fa944b1fd50fb5e994.png
    Малюнок\(\PageIndex{6}\): Трикутник з горизонтальною основою, позначеною п'ятьма і одним четвертим сантиметрами. Вгорі і ліворуч від горизонтальної сторони розташовується вершина і горизонтальна лінія витягнута вліво від основи. Від верхньої вершини до розширеної основи проводиться вертикальна пунктирна лінія і вказується символ прямого кута. Вертикальна пунктирна лінія позначається h.

    Вправа\(\PageIndex{6}\)

    1. Який вираз можна використовувати, щоб знайти, скільки кубів з довжиною краю\(\frac{1}{3}\) одиниці вписується в призму, яка становить 5 одиниць на 5 одиниць на 8 одиниць? Поясніть або покажіть свої міркування.
      • \(\left(5\cdot\frac{1}{3}\right)\cdot\left( 5\cdot\frac{1}{3}\right)\cdot\left( 8\cdot\frac{1}{3}\right)\)
      • \(5\cdot 5\cdot 8\)
      • \(\left( 5\cdot 3\right)\cdot\left( 5\cdot 3\right)\cdot\left( 8\cdot 3\right)\)
      • \(\left(5\cdot 5\cdot 8\right)\cdot\left(\frac{1}{3}\right)\)
    2. Май каже, що ми також можемо знайти відповідь, помноживши довжини країв призми, а потім помноживши результат на\(27\). Чи згодні ви з нею? Поясніть свої міркування.

    Вправа\(\PageIndex{7}\)

    Будівельник будує паркан з дерев'яних дощок\(6\frac{1}{4}\) шириною в дюйм, розташованих поруч без зазорів і перекриттів. Скільки потрібно дощок, щоб побудувати паркан довжиною 150 дюймів? Покажіть свої міркування.

    (З блоку 4.4.1)

    Вправа\(\PageIndex{8}\)

    Знайдіть значення кожного виразу. Покажіть свої міркування і перевірте свою відповідь.

    1. \(2\frac{1}{7}\div\frac{2}{7}\)
    2. \(\frac{17}{20}\div\frac{1}{4}\)

    (З блоку 4.4.1)

    Вправа\(\PageIndex{9}\)

    Розглянемо проблему: відро містить\(11\frac{2}{3}\) галони води і\(\frac{5}{6}\) наповнене. Скільки галонів води було б у повному відрі?

    Напишіть множення та рівняння ділення, щоб представити ситуацію. Потім знайдіть відповідь і покажіть свої міркування.

    (Від блоку 4.3.2)

    Вправа\(\PageIndex{10}\)

    У тренажерному залі 80 дітей. 75% носять шкарпетки. Скільки не носять шкарпетки? Якщо ви застрягли, подумайте про використання стрічкової схеми.

    (Від блоку 3.4.3)

    Вправа\(\PageIndex{11}\)

    1. Лін хоче заощадити $75 на поїздку в місто. Якщо вона зберегла $37,50 до цих пір, який відсоток своєї мети вона врятувала? Який відсоток залишається?
    2. Ной хоче заощадити 60 доларів, щоб він міг придбати квиток на концерт. Якщо він поки що заощадив 45 доларів, який відсоток своєї мети він врятував? Який відсоток залишається?

    (Від блоку 3.4.2)