Skip to main content
LibreTexts - Ukrayinska

10.1: Рецепти

  1. Last updated
  2. Save as PDF
  • Page ID
    959

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Урок

    Давайте вивчимо, як співвідношення впливають на смак рецепта.

    Вправа\(\PageIndex{1}\): Flower Pattern

    Ця квітка складається з жовтих шестикутників, червоних трапецій та зелених трикутників.

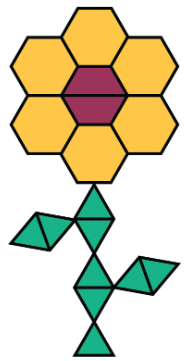
    clipboard_e7f2d02a2887428027a185c037cf9ced5.png
    Малюнок\(\PageIndex{1}\)
    1. Напишіть пропозиції, щоб описати співвідношення фігур, що складають цей візерунок.
    2. Скільки кожної фігури було б у двох примірниках цього квіткового візерунка?

    Вправа\(\PageIndex{2}\): Powdered Drink Mix

    Ось схеми, що представляють три суміші порошкоподібної суміші напою і води:

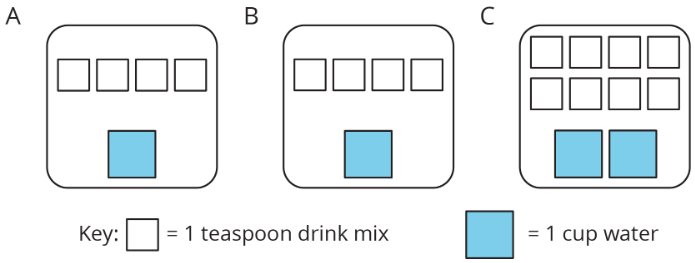
    clipboard_eb472c54d9af1200251fb65b3ba089899.png
    Рисунок\(\PageIndex{2}\): Дискретна діаграма для трьох величин, позначені A, B та C. Діаграма А містить 4 білих квадрата та 1 синій квадрат. Діаграма B має 4 білих квадрата і 1 синій квадрат. Діаграма С має 8 білих квадратів і 2 синіх квадратів. Нижче діаграма Ключ показує 1 білий квадрат дорівнює 1 чайній ложці напою суміші, а 1 синій квадрат дорівнює 1 склянці води.
    1. Як би смак суміші А порівнявся зі смаком суміші B?
    2. Скористайтеся діаграмами, щоб заповнити кожне твердження:
      1. Суміш В використовує ______ склянки води і ______ чайних ложок напою суміші. Співвідношення чашок води до чайних ложок суміші напою в суміші Б становить ________.
      2. Суміш С використовує ______ склянки води і ______ чайних ложок напою суміші. Співвідношення чашок води до чайних ложок суміші напою в суміші С становить ________.
    3. Як би смак суміші B порівнявся зі смаком суміші С?

    Ви готові до більшого?

    Спортивні напої використовують натрій (більш відомий як сіль), щоб допомогти людям заповнити електроліти. Ось етикетки харчування двох спортивних напоїв.

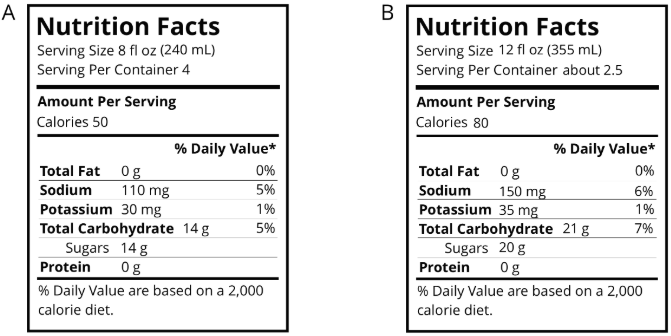
    clipboard_e8e49518edcc606cfcd9eb1b041fca57c.png
    Малюнок\(\PageIndex{3}\): Дві етикетки фактів харчування, A і B. Напій A: розмір порції 8 рідких унцій. Порцій на контейнер, 4. Кількість в одній порції: калорій, 50. Загальний жир, 0 грам; Відсоток добової норми, 0. Натрій, 110 міліграм; Відсоток добової норми, 5. Калій, 130 міліграм; Відсоток добової норми, 1. Загальна кількість вуглеводів, 14 грам; Відсоток добової норми, 5. Цукор, 14 грам. Білок, 0 грам. Відсотки добових значень засновані на дієті 2,000 калорій. Напій В: порція розміром 12 унцій рідини. Порцій на контейнер, 2,5. Кількість в одній порції: калорій, 80. Загальний жир, 0 грам; Відсоток добової норми, 0. Натрій, 150 міліграм; Відсоток добової норми, 6. Калій, 35 міліграм; Відсоток добової норми, 1. Всього вуглеводів, 21 грам; Відсоток добової норми, 7. Цукор, 20 грам. Білок, 0 грам. Відсотки добових значень засновані на дієті 2,000 калорій.
    1. Який з цих напоїв солоніше? Поясніть, як ви знаєте.
    2. Якби ви хотіли переконатися, що спортивний напій був менш солоним, ніж обидва наведені, яке співвідношення натрію та води ви б використовували?

    Вправа\(\PageIndex{3}\): Batches of Cookies

    Рецепт однієї партії печива передбачає 5 склянок борошна і 2 чайні ложки ванілі.

    1. Намалюйте схему, яка показує кількість борошна і ванілі, необхідних для двох партій печива.
    2. Скільки партій можна зробити з 15 склянками борошна і 6 чайними ложками ванілі? Покажіть додаткові партії, додавши більше інгредієнтів до вашої діаграми.
    3. Скільки борошна і ванілі вам знадобиться для 5 партій печива?
    4. Незалежно від того, чи є співвідношення чашок борошна до чайних ложок ванілі\(5:2\)\(10:4\)\(15:6\), або рецепти зроблять печиво, яке на смак однаково. Ми називаємо ці еквівалентні співвідношення.
      1. Знайдіть інше співвідношення чашок борошна до чайних ложок ванілі, яке еквівалентно цим співвідношенням.
      2. Скільки партій ви можете зробити, використовуючи це нове співвідношення інгредієнтів?

    Резюме

    Рецепт газованого соку говорить: «Змішайте 5 склянок журавлинного соку з 2 склянками газованої води».

    Щоб подвоїти цей рецепт, ми б використали 10 склянок журавлинного соку з 4 склянками газованої води. Щоб потроїти цей рецепт, ми б використали 15 склянок журавлинного соку з 6 склянками газованої води.

    На цій схемі показана одна заміс рецептури, подвійна заміс, і потрійна заміс:

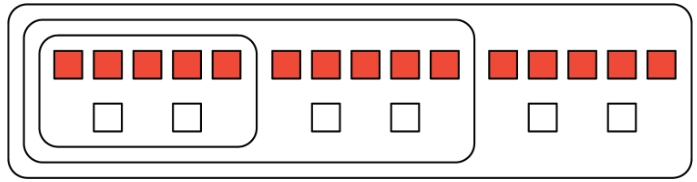
    clipboard_ee3796768798d07cac6bd0523070adff6.png
    Малюнок\(\PageIndex{4}\): Еквівалентні співвідношення рецептури газованого соку з використанням журавлинного соку і газованої води. Одна партія дорівнює 5 склянкам журавлинного соку і 2 склянкам газованої води. Дві партії дорівнюють 10 склянкам журавлинного соку і 4 склянкам газованої води. Три партії дорівнюють 15 склянкам журавлинного соку і 6 склянкам газованої води.

    Ми говоримо, що співвідношення\(5:2\)\(10:4\), і\(15:6\) рівнозначні. Незважаючи на те, що кількість кожного інгредієнта в межах однієї, подвійної або потрійної партії не однакова, вони зроблять газований сік, який на смак однаковий.

    Практика

    Вправа\(\PageIndex{4}\)

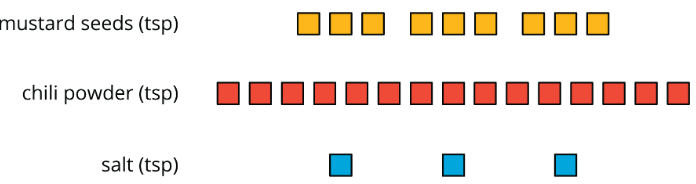
    Рецепт 1 партії суміші спецій говорить: «З'єднайте 3 чайні ложки насіння гірчиці, 5 чайних ложок порошку чилі та 1 чайну ложку солі». Скільки партій представлено на схемі? Поясніть або покажіть свої міркування.

    clipboard_e4c35e7433f49008710b3f56cc236759c.png
    Малюнок\(\PageIndex{5}\): Дискретна діаграма для трьох величин, позначені насінням гірчиці, в чайних ложках, порошку чилі, в чайних ложках і солі, в чайних Дані такі: насіння гірчиці, 9 жовтих квадратів. порошок чилі, 15 червоних квадратів. солі, 3 синіх квадрата.

    Вправа\(\PageIndex{5}\)

    Прия робить шоколадне молоко, змішавши 2 склянки молока і 5 столових ложок какао-порошку. Намалюйте схему, на якій чітко зображені дві партії її шоколадного молока.

    Вправа\(\PageIndex{6}\)

    У рецепті газованого виноградного соку співвідношення чашок газованої води до чашок концентрату виноградного соку становить 3 до 1.

    1. Знайдіть ще два співвідношення чашок газованої води до чашок концентрату соку, які б зробили суміш, яка на смак така ж, як цей рецепт.
    2. Опишіть ще одну суміш газованої води і виноградного соку, яка б на смак відрізнялася від цього рецепта.

    Вправа\(\PageIndex{7}\)

    Запишіть відсутнє число під кожною галочкою на цифровому рядку.

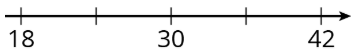
    clipboard_e1a416f71109562cc576db69fb9fca1b3.png
    Малюнок\(\PageIndex{6}\)

    (З блоку 2.1.1)

    Вправа\(\PageIndex{8}\)

    У розпліднику припадає 6 собак на кожні 5 кішок.

    1. Співвідношення собак до кішок становить ______ до ______.
    2. Співвідношення кішок до собак становить ______ до ______.
    3. На кожні ______ собаки припадає ______ кішок.
    4. Співвідношення кішок до собак ______: ______.

    (З блоку 2.1.1)

    Вправа\(\PageIndex{9}\)

    Олена має 80 одиниць кубів. Який обсяг найбільшого куба вона може побудувати з їх допомогою?

    (Від одиниці 1.6.1)

    Вправа\(\PageIndex{10}\)

    Заповніть пробіли, щоб зробити кожне рівняння істинним.

    1. \(3\cdot\frac{1}{3}=\underline{\qquad}\)
    2. \(10\cdot\frac{1}{10}=\underline{\qquad}\)
    3. \(19\cdot\frac{1}{19}=\underline{\qquad}\)
    4. \(a\cdot\frac{1}{a}=\underline{\qquad}\)

    (Поки\(a\) не дорівнює\(0\).)

    1. \(5\cdot\underline{\qquad}=1\)
    2. \(17\cdot\underline{\qquad}=1\)
    3. \(b\cdot\underline{\qquad}=1\)

    (З блоку 2.1.1)