5.2: Похідні розширено-дійсних функцій
- Page ID
- 63145
На деякий час (в §§2 і 3) ми обмежуємося розширено-реальними функціями. Нижче,\(f\) і\(g\) є реальні або розширені реальні (f,\(g : E^{1} \rightarrow E^{*}).\) Ми припускаємо, однак, що вони не постійно нескінченні на будь-якому інтервалі\((a, b), a<b\).
Якщо\(f^{\prime}(p)>0\) у якихось\(p \in E^{1},\) то
\[x<p<y\]
мається на увазі
\[f(x)<f(p)<f(y)\]
для всіх\(x, y\) в досить маленькій глобусі\(G_{p}(\delta)=(p-\delta, p+\delta).\)
Аналогічно, якщо\(f^{\prime}(p)<0,\) потім\(x<p<y\) має\(f(x)>f(p)>f(y)\) на\(x, y\) увазі для деяких\(G_{p}(\delta).\)
- Доказ
-
Якщо\(f^{\prime}(p)>0,\) випадок «0" у визначенні 1 з §1, виключається, отже
\[f^{\prime}(p)=\lim _{x \rightarrow p} \frac{\Delta f}{\Delta x}>0.\]
Отже, ми також повинні мати\(\Delta f / \Delta x>0\) для\(x\) деяких\(G_{p}(\delta)\).
Звідси випливає, що\(\Delta f\) і\(\Delta x\) мають однаковий знак в\(G_{p}(\delta);\) т. Е.
\[f(x)-f(p)>0 \text { if } x>p \text { and } f(x)-f(p)<0 \text { if } x<p.\]
(Це означає,\(f(p) \neq \pm \infty.\) чому? Звідси
\[x<p<y \Longrightarrow f(x)<f(p)<f(y),\]
як стверджується; аналогічно у випадку\(f^{\prime}(p)<0. \quad \square\)
Якщо\(f(p)\) максимальне або мінімальне значення\(f(x)\) for\(x\) в деякому\(G_{p}(\delta),\) то\(f^{\prime}(p)=0;\) тобто\(f\) має нульову похідну, або взагалі немає, на\(p.\)
Бо, по Lemma 1,\(f^{\prime}(p) \neq 0\) виключає максимум або мінімум на\(p.\) (Чому?)
Примітка 1. Таким чином,\(f^{\prime}(p)=0\) є необхідною умовою для локального максимуму або мінімуму при\(p.\) цьому недостатньо. Наприклад, якщо взагалі не\(f(x)=x^{3}, f\) має максимумів або мінімумів, але\(f^{\prime}(0)=0 .\) Для достатніх умов див. §6.
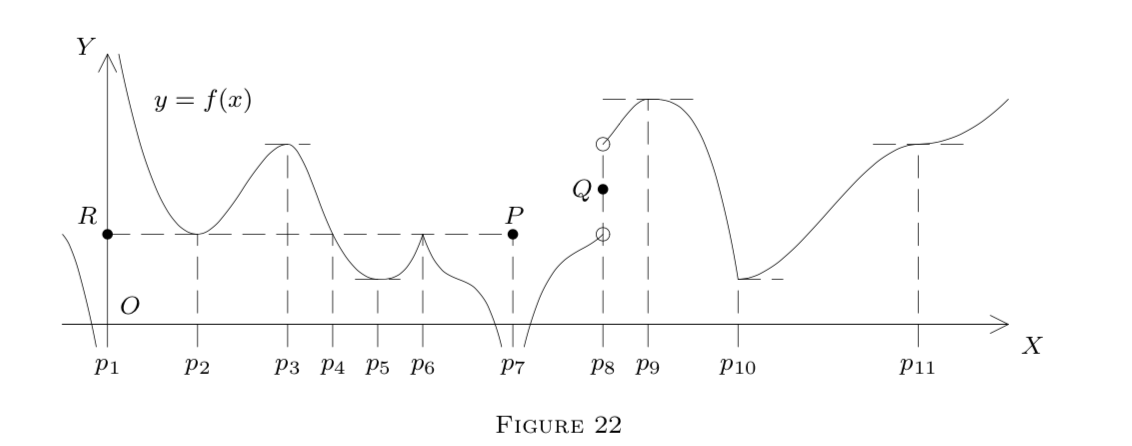
Малюнок 22 ілюструє ці факти в точках\(p_{2}, p_{3}, \ldots, p_{11}.\) Зверніть увагу, що на малюнку 22 ізольовані точки\(P, Q, R\) належать графіку.
Геометрично\(f^{\prime}(p)=0\) означає, що тангенс в\(p\) горизонтальний, або що двосторонній тангенс не існує при\(p.\)
\(f : E^{1} \rightarrow E^{*}\)Дозволяти бути відносно безперервним на інтервалі\([a, b]\), з\(f^{\prime} \neq 0\) на\((a, b).\) Потім\(f\) строго монотонний на\([a, b],\) і\(f^{\prime}\) є signconstant там (можливо 0 в a і b), з\(f^{\prime} \geq 0\) якщо\(f \uparrow,\) і\(f^{\prime} \leq 0\) якщо\(f \downarrow\).
- Доказ
-
За теоремою 2 глави 4, §8,\(f\) досягає найменшого значення\(m,\) та найбільшого значення\(M,\) в деяких точках\([a, b].\) Однак жодне не може відбуватися у внутрішній точці, бо,\(p \in(a, b),\) за наслідком 1, це означало б\(f^{\prime}(p)=0,\) суперечити нашому припущенню.
Таким чином,\(M=f(a)\) або\(M=f(b);\) на даний момент ми припускаємо,\(M=f(b)\) і\(m=f(a).\) Ми повинні мати\(m<M,\) для\(m=M\) того, щоб зробити\(f\) постійним на\([a, b]\), маючи на увазі\(f^{\prime}=0.\) Таким чином\(m=f(a)<f(b)=M.\)
Тепер давайте\(a \leq x<y \leq b\). Застосовуючи попередній аргумент до кожного з інтервалів\([a, x],[a, y],[x, y],\) і\([x, b]\) (тепер використовуючи це\(m=f(a)<f(b)=M )\), ми знаходимо, що
\[f(a) \leq f(x)<f(y) \leq f(b). \quad \text { (Why?) }\]
Таким чином, мається на\(a \leq x<y \leq b\) увазі\(f(x)<f(y);\) тобто,\(f\) збільшення\([a, b].\) Звідси\(f^{\prime}\) не може бути негативним ні в якому\(p \in[a, b],\) для, інакше, по Lemma 1,\(f\) зменшиться при\(p.\) Таким чином\(f^{\prime} \geq 0\) на\([a, b].\)
У випадку\(M=f(a)>f(b)=m,\) ми отримаємо\(f^{\prime} \leq 0\). \(\quad \square\)
Увага: Функція\(f\) може збільшуватися або зменшуватися,\(p\) навіть якщо\(f^{\prime}(p)=0.\)
Див. Примітку 1.
Якщо:\(E^{1} \rightarrow E^{*}\) є відносно безперервним\([a, b]\) і якщо\(f(a)=f(b),\) то\(f^{\prime}(p)=0\) для принаймні однієї внутрішньої точки\(p \in(a, b)\).
Бо, якщо\(f^{\prime} \neq 0\) на всіх\((a, b),\) тоді за теоремою 1,\(f\) було б строго монотонним,\([a, b],\) тому рівність\(f(a)=f(b)\) була б неможливою.
Малюнок 22 ілюструє це на інтервалах\(\left[p_{2}, p_{4}\right]\) і\(\left[p_{4}, p_{6}\right],\) при розриві\(f^{\prime}\left(p_{3}\right)=\)\(f^{\prime}\left(p_{5}\right)=0.\) A при 0 викликає явний збій на\([0, p_{2}].\)
Примітка 2. Теорема 1 і Слідство 2 тримають навіть якщо\(f(a)\) і\(f(b)\) є нескінченними, якщо безперервність інтерпретується в сенсі\(\rho^{\prime}\) метрики задачі 5 в главі 3, §11. (Теорема Вайєрштрасса 2 глави 4, §8 застосовується\(\left(E^{*}, \rho^{\prime}\right),\) з тим самим доказом.)
Нехай функції\(f, g : E^{1} \rightarrow E^{*}\) будуть відносно неперервними і кінцевими\([a, b]\) і мають похідні на\((a, b),\) з\(f^{\prime}\) і\(g^{\prime}\) ніколи обидва нескінченні в одній точці\(p \in(a, b).\) Тоді
\[g^{\prime}(q)[f(b)-f(a)]=f^{\prime}(q)[g(b)-g(a)] \text { for at least one } q \in(a, b).\]
- Доказ
-
Нехай\(A=f(b)-f(a)\) і\(B=g(b)-g(a).\) Ми повинні показати, що\(A g^{\prime}(q)=B f^{\prime}(q)\) для деяких\(q \in(a, b)\). Для цього розглянемо функцію\(h=A g-B f\). Це відносно безперервний і кінцевий на\([a, b],\) як є,\(g\) а\(f.\) також,
\[h(a)=f(b) g(a)-g(b) f(a)=h(b) . \quad \text { (Verify!) }\]
Таким чином, наслідком 2,\(h^{\prime}(q)=0\) для деяких\(q \in(a, b).\) Тут, за теоремою 4 §1,\(h^{\prime}=(A g-B f)^{\prime}=A g^{\prime}-B f^{\prime}.\) (Це є законним, бо, за припущенням,\(f^{\prime}\) і\(g^{\prime}\) ніколи не стають нескінченними, тому не відбуваються невизначені межі.) Таким чином\(h^{\prime}(q)=A g^{\prime}(q)-B f^{\prime}(q)=0,\) і (1) слід. \(\quad \square\)
Якщо\(f : E^{1} \rightarrow E^{1}\) є відносно безперервним на\([a, b]\) з похідною,\((a, b),\) то
\[f(b)-f(a)=f^{\prime}(q)(b-a) \text { for at least one } q \in(a, b).\]
- Доказ
-
Візьміть\(g(x)=x\) в теоремі 2, так\(g^{\prime}=1\) далі\(E^{1}. \square\)
Примітка 3. Геометрично,
\[\frac{f(b)-f(a)}{b-a}\]
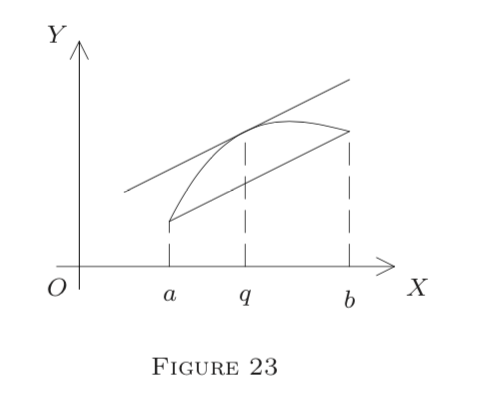
- нахил січної наскрізь\((a, f(a))\)\((b, f(b)),\) і\(f^{\prime}(q)\) є нахилом дотичної лінії при\(q.\) цьому Слідство 3 стверджує, що січна паралельна дотичній в деякій проміжній точці\(q;\) див. Рис. 23. Теорема 2 стверджує те ж саме для кривих, заданих параметрично:\(x=f(t), y=g(t)\).
\(f\)Дозволяти бути як в Слідство 3. Тоді
(i)\(f\) є постійним на\([a, b]\) iff\(f^{\prime}=0\) увімкнено\((a, b)\);
(ii)\(f \uparrow\) на\([a, b]\) iff\(f^{\prime} \geq 0\) на\((a, b);\) і
(iii)\(f \downarrow\) на\([a, b]\)\(f^{\prime} \leq 0\) вимкнено\((a, b)\).
- Доказ
-
Нехай\(f^{\prime}=0\) on\((a, b).\) Якщо\(a \leq x \leq y \leq b,\) застосувати Слідство 3 до інтервалу,\([x, y]\) щоб отримати
\[f(y)-f(x)=f^{\prime}(q)(y-x) \text { for some } q \in(a, b) \text { and } f^{\prime}(q)=0.\]
При цьому\(f(y)-f(x)=0\) для\(x, y \in[a, b],\) так\(f\) є постійним.
Решта залишається читачеві. \(\quad \square\)
\(f : E^{1} \rightarrow E^{1}\)Дозволяти бути відносно безперервними і строго монотонними на проміжку\(I \subseteq E^{1}\). Нехай\(f^{\prime}(p) \neq 0\) в деякій внутрішній точці\(p \in I.\) Потім обернена функція\(g=f^{-1}\) (з\(f\) обмеженою до)\(I)\) має похідну в\(q=f(p),\) і
\[g^{\prime}(q)=\frac{1}{f^{\prime}(p)}.\]
(Якщо\(f^{\prime}(p)=\pm \infty,\) тоді\(g^{\prime}(q)=0.)\)
- Доказ
-
За теоремою 3 глави 4, §9,\(g=f^{-1}\) є строго монотонним і відносно безперервним на\(f[I],\) собі інтервал. Якщо\(p\) це інтер'єр,\(I,\) то\(q=f(p)\) це інтер'єр до\(f[I].\) (Чому?)
Тепер, якщо\(y \in f[I],\) ми встановимо
\[\Delta g=g(y)-g(q), \Delta y=y-q, x=f^{-1}(y)=g(y), \text { and } f(x)=y\]
і отримати
\[\frac{\Delta g}{\Delta y}=\frac{g(y)-g(q)}{y-q}=\frac{x-p}{f(x)-f(p)}=\frac{\Delta x}{\Delta f} \text { for } x \neq p.\]
Тепер, якщо\(y \rightarrow q,\) безперервність\(g\) at\(q\) дає\(g(y) \rightarrow g(q);\) тобто,\(x \rightarrow p.\) Також,\(x \neq p\) iff\(y \neq q\), for\(f\) і\(g\) є функціями один до одного. Таким чином, ми можемо замінити\(y=f(x)\) або\(x=g(y)\) отримати
\[g^{\prime}(q)=\lim _{y \rightarrow q} \frac{\Delta g}{\Delta y}=\lim _{x \rightarrow p} \frac{\Delta x}{\Delta f}=\frac{1}{\lim _{x \rightarrow p}(\Delta f / \Delta x)}=\frac{1}{f^{\prime}(p)},\]
де ми використовуємо конвенцію,\(\frac{1}{\infty}=0\) якщо\(f^{\prime}(p)=\infty. \quad \square\)
(А) Нехай
\[f(x)=\log _{a}|x| \text { with } f(0)=0.\]
Нехай\(p>0.\) тоді\((\forall x>0)\)
\[\begin{aligned} \Delta f &=f(x)-f(p)=\log _{a} x-\log _{a} p=\log _{a}(x / p) \\ &=\log _{a} \frac{p+(x-p)}{p}=\log _{a}\left(1+\frac{\Delta x}{p}\right). \end{aligned}\]
Таким чином
\[\frac{\Delta f}{\Delta x}=\log _{a}\left(1+\frac{\Delta x}{p}\right)^{1 / \Delta x}.\]
Тепер давайте\(z=\Delta x / p.\) (Чому ця заміна допустима?) Потім за допомогою формули
\[\lim _{z \rightarrow 0}(1+z)^{1 / z}=e \quad \text { (see Chapter 4, §2, Example (C)) }\]
і безперервність функції журналу і живлення, отримаємо
\[f^{\prime}(p)=\lim _{x \rightarrow p} \frac{\Delta f}{\Delta x}=\lim _{z \rightarrow 0} \log _{a}\left[(1+z)^{1 / z}\right]^{1 / p}=\log _{a} e^{1 / p}=\frac{1}{p} \log _{a} e.\]
Та ж формула призводить також, якщо\(p<0,\) тобто,\(|p|=-p.\) At\(p=0, f\) має\(( \pm \infty)\) лише односторонні похідні (перевірити!) , так\(f^{\prime}(0)=0\) за визначенням 1 в §1.
(B) Оберненою\(_{a}\) функцією журналу є експоненціальна\(g : E^{1} \rightarrow E^{1},\) з
\[g(y)=a^{y} \quad(a>0, a \neq 1).\]
За теоремою 3 ми маємо
\[\left(\forall q \in E^{1}\right) \quad g^{\prime}(q)=\frac{1}{f^{\prime}(p)}, p=g(q)=a^{q}.\]
Таким чином
\[g^{\prime}(q)=\frac{1}{\frac{1}{p} \log _{a} e}=\frac{p}{\log _{a} e}=\frac{a^{q}}{\log _{a} e}.\]
Символічно,
\[\left(\log _{a}|x|\right)^{\prime}=\frac{1}{x} \log _{a} e(x \neq 0) ; \quad\left(a^{x}\right)^{\prime}=\frac{a^{x}}{\log _{a} e}=a^{x} \ln a.\]
Зокрема, якщо у\(a=e,\) нас є\(\log _{e} a=1\) і,\(\log _{a} x=\ln x ;\) отже,
\[(\ln |x|)^{\prime}=\frac{1}{x}(x \neq 0) \quad \text { and } \quad\left(e^{x}\right)^{\prime}=e^{x} \quad\left(x \in E^{1}\right).\]
(C) Функція потужності\(g :(0,+\infty) \rightarrow E^{1}\) задається
\[g(x)=x^{a}=\exp (a \cdot \ln x) \text { for } x>0 \text { and fixed } a \in E^{1}.\]
За правилом ланцюга (§1, теорема 3) отримаємо
\[g^{\prime}(x)=\exp (a \cdot \ln x) \cdot \frac{a}{x}=x^{a} \cdot \frac{a}{x}=a \cdot x^{a-1}.\]
Таким чином, ми маємо символічну формулу
\[\left(x^{a}\right)^{\prime}=a \cdot x^{a-1} \text { for } x>0 \text { and fixed } a \in E^{1}.\]
Якщо\(f : E^{1} \rightarrow E^{*}\) є відносно безперервним і має похідну на інтервалі I, то\(f^{\prime}\) має властивість Дарбу (Глава 4, §9) на\(I.\)
- Доказ
-
Дозвольте\(p, q \in I\) і\(f^{\prime}(p)<c<f^{\prime}(q).\)\(g(x)=f(x)-c x.\)\(g^{\prime} \neq 0\) покладіть Припустіть\((p, q)\) і знайдіть протиріччя теоремі 1. Подробиці залишаються читачеві. \(\quad \square\)
