4.1: Основні визначення
- Page ID
- 63033
Тепер ми розглянемо функції, домени та діапазони яких встановлюються в деяких фіксованих (але в іншому випадку довільних) метричних просторах\((S, \rho)\) і\(\left(T, \rho^{\prime}\right),\) відповідно. пишемо
\[f : A \rightarrow\left(T, \rho^{\prime}\right)\]
для функції\(f\) з\(D_{f}=A \subseteq(S, \rho)\) і\(D_{f}^{\prime} \subseteq\left(T, \rho^{\prime}\right) . \quad S\) називається доменним простором,\(T\) а простір діапазону,\(f .\)
І. З огляду на таку функцію, нам часто доводиться досліджувати її «локальну поведінку» поблизу якоїсь точки.\(p \in S .\) Зокрема, якщо\(p \in A=D_{f}(\text { so that } f(p) \text { is defined) we }\) може запитати: Чи можна зробити значення\(f(x)\) функції такими близькими, як нам подобається (\(" \varepsilon -\)поблизу»), щоб,\(f(p)\) тримаючись\(x\) досить близько \(\left(\text { "close }^{\prime \prime}\right)\)\(p,\)тобто всередині деякого досить маленького глобуса\(G_{p}(\delta) ?\) Якщо це так, ми говоримо, що\(f\) є безперервним в\(p .\) Точніше, ми формулюємо наступне визначення.
\(A \subseteq(S, \rho),\)Функція\(f : A \rightarrow\left(T, \rho^{\prime}\right),\) з, як кажуть, безперервна при\(p\) iff\(p \in A\) і, крім того, для кожного\(\varepsilon>0\) (незалежно від того, наскільки маленьким) є\(\delta>0\) така, що\(\rho^{\prime}(f(x), f(p))<\varepsilon\) для всіх символів\(x \in A \cap G_{p}(\delta) .\) In,
\[(\forall \varepsilon>0)(\exists \delta>0)\left(\forall x \in A \cap G_{p}(\delta)\right)\left\{\begin{array}{l}{\rho^{\prime}(f(x), f(p))<\varepsilon, \text { or }} \\ {f(x) \in G_{f(p)}(\varepsilon)}\end{array}\right.\]
Якщо\((1)\) не вдається, ми говоримо, що\(f\) є\(p\) переривчастим в\(p\) і називаємо точку розриву\(f .\) Це також так, якщо\(p \notin A\) (\(f(p)\)оскільки не визначено).
Якщо\((1)\) тримає для кожного р у множині\(B \subseteq A,\) ми говоримо, що\(f\) є безперервним на\(B .\) Якщо це так для\(B=A,\) ми просто говоримо, що\(f\) є безперервним.
Іноді ми вважаємо за краще тримати\(x\) поруч,\(p\) але відрізняється від\(p .\) Ми потім замінити\(G_{p}(\delta)\)\((1)\) на набір,\(G_{p}(\delta)-\{p\},\) тобто глобус без його центру, позначається\(G_{\neg p}(\delta)\) і називається віддалений\(\delta\) -глобус про\(p .\) Це навіть необхідно, якщо\(p \notin D_{f}\). Заміна\(f(p)\)\((1)\) на деякі\(q \in T,\) ми потім привели до наступного визначення.
Враховуючи,\(f : A \rightarrow\left(T, \rho^{\prime}\right), A \subseteq(S, \rho), p \in S,\) і\(q \in T,\) ми говоримо, що,\(f(x)\)\(q\) як\(x\) правило, як правило,\(p(f(x) \rightarrow q \text { as } x \rightarrow p)\) iff для кожного\(\varepsilon>0\) є\(\delta>0\) таке, що\(\rho^{\prime}(f(x), q)<\varepsilon\) для всіх символів\(x \in A \cap G_{\neg p}(\delta) .\) In,
\[(\forall \varepsilon>0)(\exists \delta>0)\left(\forall x \in A \cap G_{\neg p}(\delta)\right) \quad\left\{\begin{array}{l}{\rho^{\prime}(f(x), q)<\varepsilon, \text { i.e. }} \\ {f(x) \in G_{q}(\varepsilon)}\end{array}\right.\]
Це означає, що\(f(x)\) є\(\varepsilon\) -close to\(q\)\(x\) when is\(\delta\) -close to\(p\) and\(x \neq p\).
Якщо\((2)\) тримає для деяких\(q,\) ми\(q\) називаємо ліміт\(f\) at\(p .\) Такого не може бути\(q\). Потім ми говоримо, що не\(f\) має межі\(p,\) або що ця межа не існує. Якщо є тільки один такий\(q(\text { for a given } p),\) пишемо\(q=\lim _{x \rightarrow p} f(x) .\)
Примітка 1. Формула (2) тримає «вакуумно» (див. Розділ 1,8 §§1-3, кінцеве зауваження), якщо\(A \cap G_{\neg p}(\delta)=\emptyset\) для деяких\(\delta>0 .\) Тоді будь-який\(q \in T\) є межею,\(p,\) тому межа існує, але не є унікальною. (Відкидаємо випадок, коли\(T\) є синглтон.)
Примітка 2. Однак унікальність забезпечується, якщо\(A \cap G_{\neg p}(\delta) \neq \emptyset\) для всіх\(\delta>0,\), як ми доведемо нижче.
Зауважте, що за наслідком 6 глави 3, §14, множинні\(A\) кластери на\(p\) iff
\[(\forall \delta>0) \quad A \cap G_{\neg p}(\delta) \neq \emptyset . \quad(\text { Explain! })\]
Таким чином, ми маємо наступний наслідок.
Якщо\(A\) кластери\(p\) в\((S, \rho),\) то функція\(f : A \rightarrow\left(T, p^{\prime}\right)\) може мати максимум одну межу на\(p ;\) тобто.
\[\lim _{x \rightarrow p} f(x) \text{ is unique (if it exists).}\]
Зокрема, це стосується якщо\(A \supseteq(a, b) \subset E^{1}(a<b)\) і\(p \in[a, b]\).
- Доказ
-
Припустимо,\(f\) має\(t w o\) обмеження,\(q\) і\(r,\)\(p .\) у власності Hausdorff,
\[G_{q}(\varepsilon) \cap G_{r}(\varepsilon)=\emptyset \quad \text{ for some } \varepsilon>0.\]
Крім того,\((2),\) існують\(\delta^{\prime}, \delta^{\prime \prime}>0\) такі, що
\[\begin{array}{ll}{\left(\forall x \in A \cap G_{\neg p}\left(\delta^{\prime}\right)\right)} & {f(x) \in G_{q}(\varepsilon) \text { and }} \\ {\left(\forall x \in A \cap G_{\neg p}\left(\delta^{\prime \prime}\right)\right)} & {f(x) \in G_{r}(\varepsilon)}\end{array}\]
Нехай\(\delta=\min \left(\delta^{\prime}, \delta^{\prime \prime}\right) .\) Тоді для\(x \in A \cap G_{\neg p}(\delta), f(x)\) є в обох\(G_{q}(\varepsilon)\) і\(G_{r}(\varepsilon)\), і таке\(x\) існує з\(A \cap G_{\neg p}(\delta) \neq \emptyset\) припущення.
Але це неможливо, так як\(G_{q}(\varepsilon) \cap G_{r}(\varepsilon)=\emptyset\)\((\text { a contradiction!). } \square\)
Щодо інтервалів див. Розділ 3, §14, Приклад (\(\mathrm{h} )\).
\(f\)є безперервним при\(p\left(p \in D_{f}\right)\) iff\(f(x) \rightarrow f(p)\) газу\(x \rightarrow p\).
- Доказ
-
Пряме доказ з визначень залишається читачеві.
Примітка 3. У формулі\((2),\) ми виключили випадок,\(x=p\) припускаючи, що\(x \in A \cap G_{\neg p}(\delta) .\) Це робить поведінку\(f\) при\(p\) собі неактуальною. Таким чином, для існування межі\(q\) на\(p,\) ньому не має значення, чи\(p \in D_{f}\) чи\(f(p)=q .\) Але обидві умови потрібні для безперервності на\(p\) (див. Наслідок 2 та Визначення 1\()\).
Примітка 4. Зауважте, що якщо\((1)\) або\((2)\) тримає для деяких,\(\delta,\) це, безумовно, тримає для будь-якого\(\delta^{\prime} \leq \delta .\) Таким чином, ми завжди можемо вибрати\(\delta\) настільки малі, як нам подобається. Більше того, як\(x\) це обмежено,\(G_{p}(\delta),\) ми можемо ігнорувати або змінювати за бажанням значення функції\(f(x)\) для\(x \notin G_{p}(\delta)\) («локальний символ поняття межі»).
ІІ. Ліміти в Е*. Якщо\(S\) або\(T\) є\(E^{*}\left(\text { or } E^{1}\right),\) ми можемо дозволити\(x \rightarrow \pm \infty\) або\(f(x) \rightarrow \pm \infty .\) Для точного визначення, ми переписуємо з\((2)\) точки зору\(globes\)\(G_{p}\) і\(G_{q} :\)
\[\left(\forall G_{q}\right)\left(\exists G_{p}\right)\left(\forall x \in A \cap G_{\neg p}\right) \quad f(x) \in G_{q}.\]
Це має сенс також, якщо\(p=\pm \infty\) або\(q=\pm \infty .\) Нам потрібно використовувати лише наші конвенції щодо\(G_{ \pm \infty},\) або\(\rho^{\prime}\) метрики,\(E^{*},\) як пояснено у розділі 3, §11.
Наприклад, розглянемо
\[^{\prime \prime}f(x) \rightarrow q \text{ as } x \rightarrow+\infty^{\prime \prime}\left(A \subseteq S=E^{*}, p=+\infty, q \in\left(T, \rho^{\prime}\right)\right).\]
Тут\(G_{p}\) має форму\((a,+\infty], a \in E^{1},\) і\(G_{\neg p}=(a,+\infty),\) поки\(G_{q}=G_{q}(\varepsilon)\), як зазвичай. Відзначивши\(x \in G_{\neg p}\) це означає, що\(x>a\left(x \in E^{1}\right),\) ми можемо переписати\(\left(2^{\prime}\right)\) як
\[(\forall \varepsilon>0)\left(\exists a \in E^{1}\right)(\forall x \in A | x>a) \quad f(x) \in G_{q}(\varepsilon), \text{ or } \rho^{\prime}(f(x), q)<\varepsilon.\]
Це означає, що\(f(x)\) стає довільно близьким до\(q\) для великих\(x(x>a)\).
Далі розглянемо\(^{4} f(x) \rightarrow+\infty\) як\(x \rightarrow-\infty\) "Тут\(G_{\neg p}=(-\infty, a)\) і\(G_{q}=(b,+\infty] .\) Таким чином формулу\(\left(2^{\prime}\right)\) дає (з\(S=T=E^{*},\) і\(x\) варіюючи над\(E^{\mathrm{i}} )\)
\[\left(\forall b \in E^{1}\right)\left(\exists a \in E^{1}\right)(\forall x \in A | x<a) \quad f(x)>b;\]
аналогічно і в інших випадках, які ми залишаємо читачеві.
Примітка 5. У\((3),\) нас може взяти\(A=N\) (натуральні). Потім\(f : N \rightarrow\left(T, \rho^{\prime}\right)\) послідовність у\(T .\) письмовій формі\(m\) для\(x,\) набору\(u_{m}=f(m)\) та\(a=k \in N\) отримання
\[(\forall \varepsilon>0)(\exists k)(\forall m>k) \quad u_{m} \in G_{q}(\varepsilon) ; \text{ i.e., } \rho^{\prime}\left(u_{m}, q\right)<\varepsilon.\]
Це збігається з нашим визначенням межі\(q\) послідовності\(\left\{u_{m}\right\}\) (див. Розділ 3, §14). Таким чином, межі послідовностей є окремим випадком обмежень функцій. Теореми про послідовності можна отримати з тих на функціях\(f : A \rightarrow\left(T, \rho^{\prime}\right)\), просто взявши\(A=N\) і\(S=E^{*}\) як зазначено вище.
Примітка 6. Формули\((3)\) і мають\((4)\) сенс також, якщо\(S=E^{1}\) (відповідно,\(S=T=E^{1} )\) оскільки вони не передбачають жодної згадки про\(\pm \infty .\) Ми будемо використовувати такі формули також для функцій\(f : A \rightarrow T,\) з\(A \subseteq S \subseteq E^{1}\) або\(T \subseteq E^{1},\) в залежності від випадку.
ІІІ. Відносні межі та безперервність. Іноді бажаний результат\((1)\) або\((2)\) не тримається в повному обсязі, а тільки з\(A\) заміною на менший набір\(B \subseteq A\). Таким чином, ми можемо мати
\[(\forall \varepsilon>0)(\exists \delta>0)\left(\forall x \in B \cap G_{\neg p}(\delta)\right) \quad f(x) \in G_{q}(\varepsilon).\]
У цьому випадку називаємо\(q\) відносну\(f\) межу at\(p\) over\(B\) і пишемо
\["f(x) \rightarrow q \text{ as } x \rightarrow p \text{ over } B"\]
або
\[\lim _{x \rightarrow p, x \in B} f(x)=q \quad(\text { if } q \text { is unique });\]
\(B\)називається шлях, по якому\(x\) має тенденцію до\(p .\) Якщо, крім того,\(p \in D_{f}\) і\(q=f(p),\) ми говоримо, що\(f\) відносно безперервний на\(p\) більш\(B ;\) потім\((1)\) тримає з\(A\) замінені на\(B\). Знову ж таки, якщо це тримає для кожного\(p \in B,\) ми говоримо, що\(f\) є відносно безперервним на\(B .\) Ясно, якщо\(B=A=D_{f},\) це дає звичайні (невідносні) межі та безперервність. При цьому відносні межі і безперервність є більш загальними.
Зауважте, що для обмежень над\(B, x\) контуром вибирається\(B-\{p\}\) лише\(B\) або лише. Таким чином, поведінка\(f\) зовні\(B\) стає неактуальною, і тому ми можемо довільно перевизначити\(f\) на\(-B .\) Наприклад, якщо\(p \notin B\) але\(\lim _{x \rightarrow p, x \in B} f(x)=q\) існує, ми можемо визначити,\(f(p)=q,\) таким чином, роблячи\(f\) відносно безперервним в\(p(\text { over } B) .\) Ми також можемо замінити\((S, \rho)\) на \((B, \rho)(\text { if } p \in B),\)або\(f\) обмежити,\(B,\) тобто замінити\(f\) функцією,\(g : B \rightarrow\left(T, \rho^{\prime}\right)\) визначеною\(g(x)=f(x)\) for\(x \in B\) (коротко,\(g=f\) на\(B )\).
Особливо важливим випадком є
\[A \subseteq S \subseteq E^{*}, \text{ e.g., } S=E^{1}.\]
Тоді нерівності визначаються\(S,\) таким чином, ми можемо прийняти
\[B=\{x \in A | x<p\} \text{ (points in } A, \text{ preceding } p).\]
Потім, пишемо\(G_{q}\) для\(G_{q}(\varepsilon)\) і\(a=p-\delta,\) отримуємо з формули\((2)\)
\[\left(\forall G_{q}\right)(\exists a<p)(\forall x \in A | a<x<p) \quad f(x) \in G_{q}.\]
Якщо\((5)\) тримає, ми називаємо\(q\) лівий ліміт\(f\) at\(p\) і пишемо
\["f(x) \rightarrow q \text{ as } x \rightarrow p^{-}" \quad\left(" x \text { tends to } p \text{ from the left}^{\prime}\right).\]
Якщо, крім того,\(q=f(p),\) ми говоримо, що\(f\) залишається безперервним на\(p .\) Аналогічно, приймаючи
\[B=\{x \in A | x>p\},\]
ми отримуємо правильні межі та безперервність. пишемо
\[f(x) \rightarrow q \text{ as } x \rightarrow p^{+}\]
iff\(q\) - це права межа\(f\) at\(p,\) тобто, якщо\((5)\) утримується з усіма нерівностями, зворотними.
Якщо множина\(B\) в питанні кластерів\(p,\) на відносній межі (якщо така є) є унікальною. Потім позначаємо ліву і праву межу, відповідно, по\(f\left(p^{-}\right)\) і\(f\left(p^{+}\right),\) і пишемо
\[\lim _{x \rightarrow p^{-}} f(x)=f\left(p^{-}\right) \text{ and } \lim _{x \rightarrow p^{+}} f(x)=f\left(p^{+}\right).\]
З попереднім позначенням, якщо\(f(x) \rightarrow q\) як\(x \rightarrow p\) над контуром,\(B,\)\(D,\) а також над тим\(f(x) \rightarrow q\), як\(x \rightarrow p\) закінчено\(B \cup D\).
Отже, якщо\(D_{f} \subseteq E^{*}\) і у\(p \in E^{*},\) нас є
\[q=\lim _{x \rightarrow p} f(x) \text{ iff } q=f\left(p^{-}\right)=f\left(p^{+}\right) . \quad(\text { Exercise! })\]
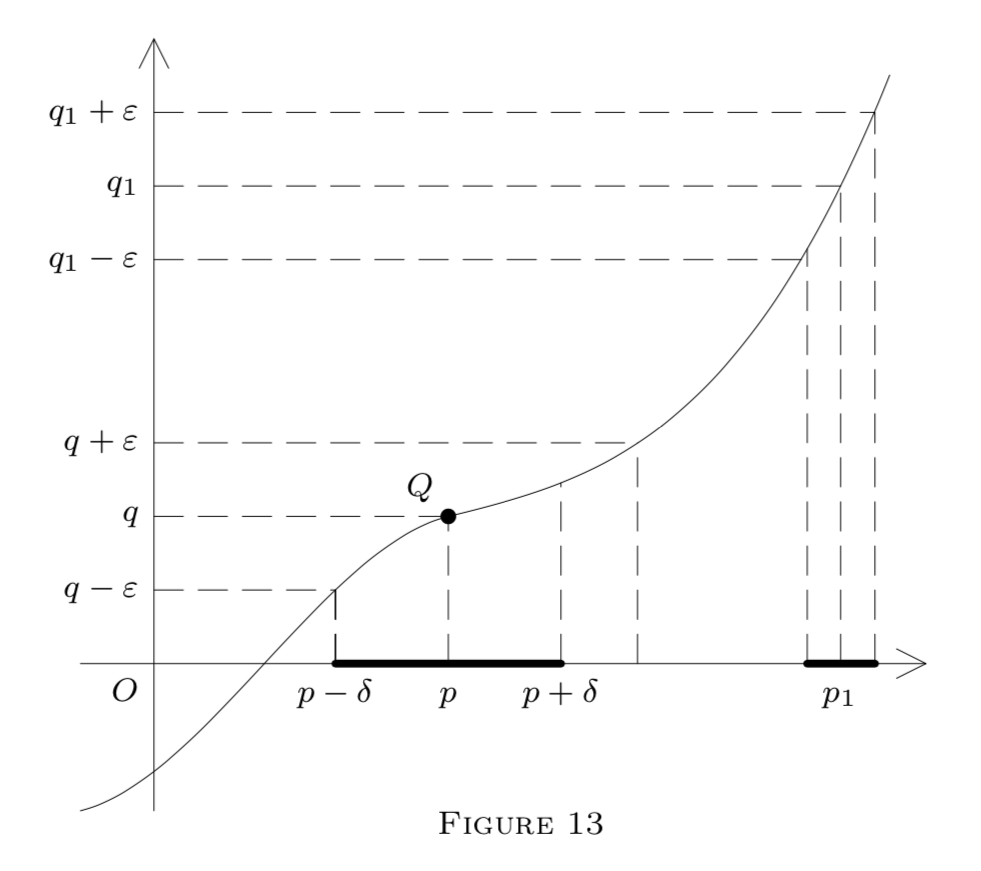
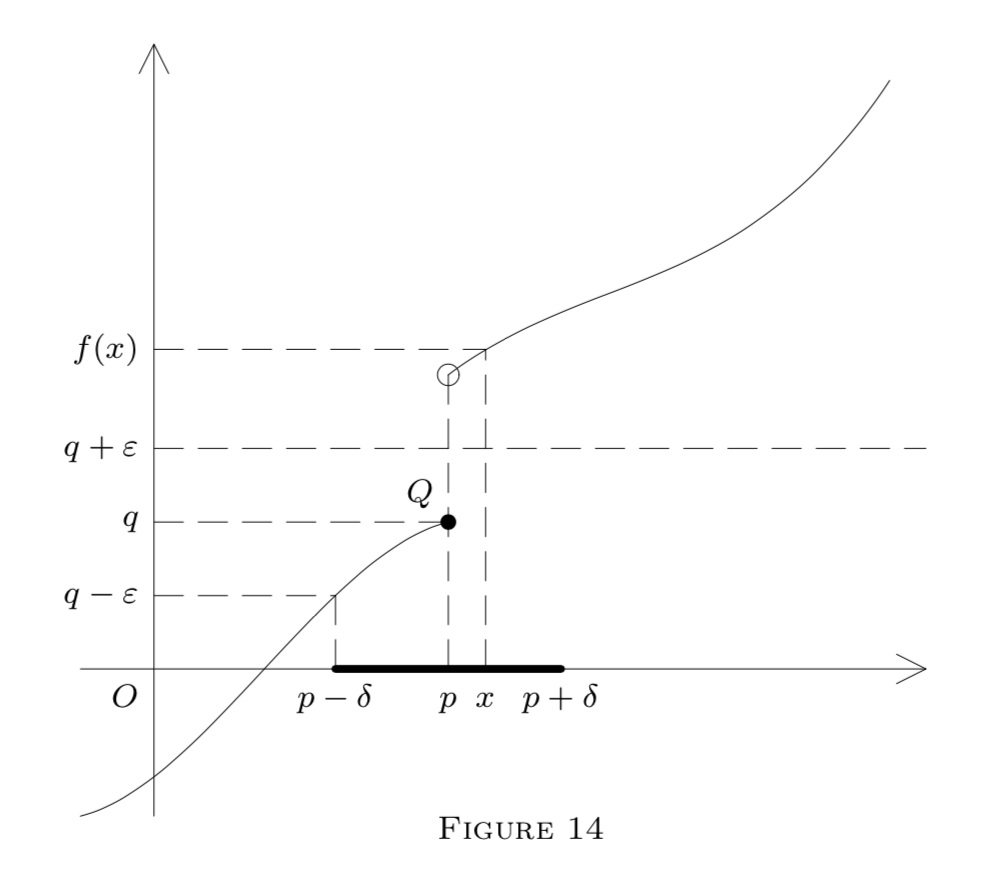
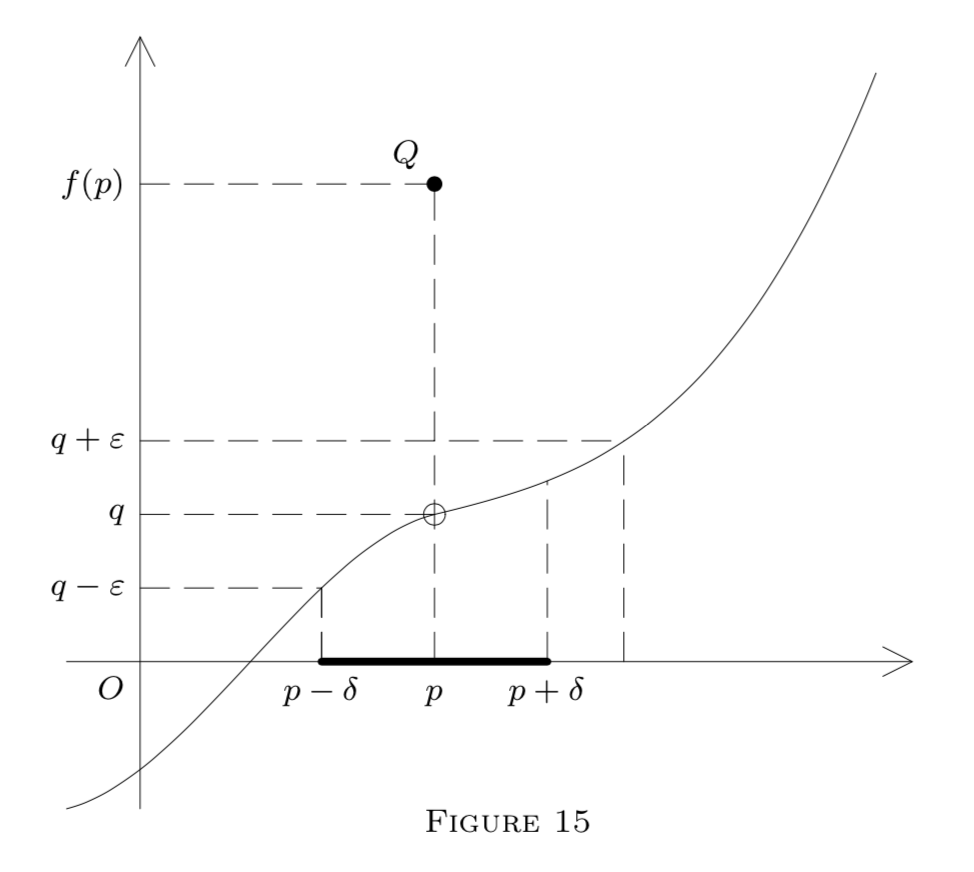
Тепер ми проілюструємо наші визначення діаграмою в\(E^{2}\) представленні функції\(f : E^{1} \rightarrow E^{1}\) за її графіком, тобто вказує\((x, y)\) такі, що\(y=f(x)\).
Тут
\[G_{q}(\varepsilon)=(q-\varepsilon, q+\varepsilon)\]
інтервал на\(y\) -осі. Пунктирні лінії показують, як побудувати інтервал
\[(p-\delta, p+\delta)=G_{p}\]
на\(x\) -осі, задовольняючи формулу\((1)\) в\(13,\) формулах малюнка\((5)\) та\((6)\) на малюнку\(14,\) або\((2)\) формулі\(15 .\) на\(Q\) малюнку Точка на кожній діаграмі належить до графіка; тобто,\(Q=(p, f(p)) .\) На малюнку\(13, f\) є безперервним при\(p(\text { and also at }\) \(p_{1}\)). Однак він є лише лівим безперервним на\(p\) малюнку,\(14,\) і це переривчастий на\(p\) малюнку,\(15,\) хоча\(f\left(p^{-}\right)\) і\(f\left(p^{+}\right)\) існує. (Чому?)
(а)\(f : A \rightarrow T\) Дозволяти бути постійною на\(B \subseteq A ;\) тобто
\[f(x)=q \text{ for a fixed } q \in T \text{ and all } x \in B.\]
Потім\(f\) є відносно безперервним на\(B,\) і\(f(x) \rightarrow q\) як\(x \rightarrow p\)\(B,\) на кожному\(p .\) (дано\(\varepsilon>0,\) взяти довільний\(\delta>0\). Тоді
\[\left(\forall x \in B \cap G_{\neg p}(\delta)\right) \quad f(x)=q \in G_{q}(\varepsilon),\]
як потрібно; аналогічно для безперервності.)
(b) Нехай\(f\) буде карта\(i\) ідентичності на\(A \subset(S, \rho) ;\) тобто,
\[(\forall x \in A) \quad f(x)=x.\]
Потім, дано\(\varepsilon>0,\) взяти,\(\delta=\varepsilon\) щоб отримати, для\(p \in A\),
\[\left(\forall x \in A \cap G_{p}(\delta)\right) \quad \rho(f(x), f(p))=\rho(x, p)<\delta=\varepsilon.\]
Таким чином, шляхом\((1), f\) є безперервним при будь-якому\(p \in A,\) звідси на\(A\).
(c)\(f : E^{1} \rightarrow E^{1}\) Визначити
\[f(x)=1 \text{ if } x \text{ is rational, and } f(x)=0 \text{ otherwise.}\]
(Це функція Діріхле, названа так на честь Йоганна Петра Густава Лежена Діріхле.)
Яким би маленьким не\(\delta\) був, земна куля
\[G_{p}(\delta)=(p-\delta, p+\delta)\]
(навіть віддалений глобус) містить як раціональні, так і ірраціональні. Таким чином, як\(x\) змінюється протягом\(G_{\neg p}(\delta), f(x)\) бере на себе обидва значення, 0 і\(1,\) багато разів і так виходить з будь-якого\(G_{q}(\varepsilon),\) з\(q \in E^{1}, \varepsilon<\frac{1}{2}\).
Отже, для будь-якої\(q, p \in E^{1},\) формули\((2)\) не вдається, якщо ми\(\varepsilon=\frac{1}{4},\) беремо сказати. Таким чином, не\(f\) має обмежень ні в якому\(p \in E^{1}\) і, отже, є переривчастим скрізь! Однак\(f\) є відносно безперервним на\(R\) множині всіх раціональних прикладу\((\mathrm{a})\).
(d) Визначити\(f : E^{1} \rightarrow E^{1}\) за
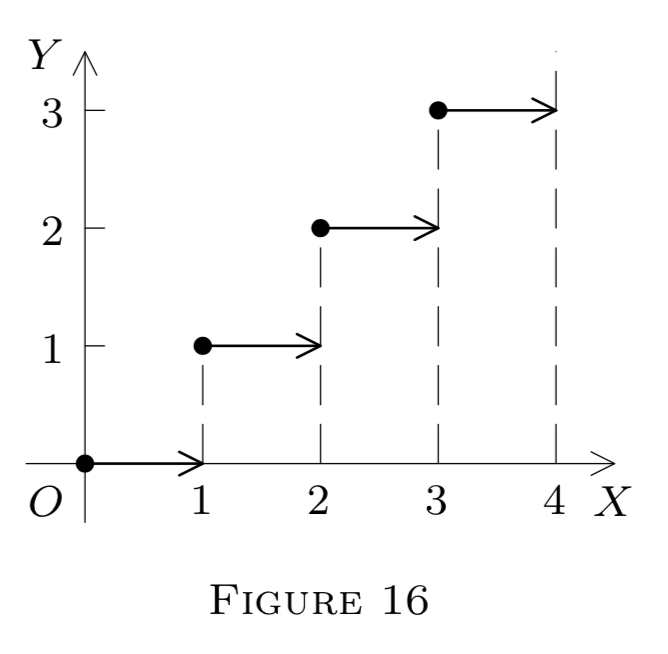
\[f(x)=[x](=\text { the integral part of } x ; \text { see Chapter } 2, §10).\]
Таким чином,\(f(x)=0\)\(x \in[0,1), f(x)=1\) для\(x \in[1,2),\) і т.д. потім\(f\) переривчастий при\(p\) якщо\(p\) є цілим числом (чому?) але безперервно при будь-якому іншому\(p\left(\text { restrict } f \text { to a small } G_{p}(\delta) \text { so as to make it constant) }\right.\)
Однак ліві та праві межі існують у кожного,\(p \in E^{1},\) навіть якщо\(p=\)\(n(\text { an integer }) .\) насправді,
\[f(x)=n, x \in(n, n+1)\]
і
\[f(x)=n-1, x \in(n-1, n),\]
отже,\(f\left(n^{+}\right)=n\) і\(f\left(n^{-}\right)=\)\(n-1 ; f\) є правильним безперервним на\(E^{1} .\) Див. Рисунок\(16 .\)
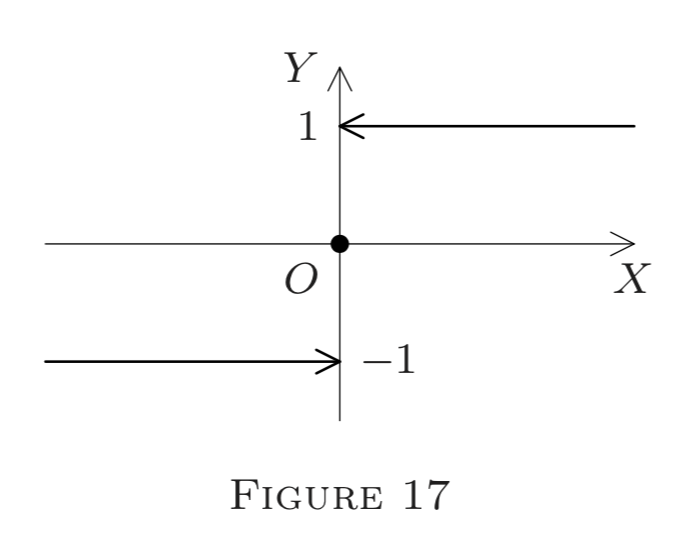
(е) Визначити\(f : E^{1} \rightarrow E^{1}\) за
\[f(x)=\frac{x}{|x|} \text{ if } x \neq 0, \text{ and } f(0)=0.\]
(Це так звана сигнум-функція, часто позначається sgn.)
Потім (рис. 17)\()\)
\[f(x)=-1 \text{ if } x<0\]
і
\[f(x)=1 \text{ if } x>0.\]
Таким чином, як і в (d), ми робимо висновок, що\(f\) є переривчастим в,\(0,\) але безперервно на кожному\(p \neq 0 .\) Також,\(f\left(0^{+}\right)=1\) і\(f\left(0^{-}\right)=-1 .\) Перевизначення\(f(0)=1\) або\(f(0)=-1,\) ми можемо зробити\(f\) право (відповідно, ліворуч) безперервним в\(0,\) але не обидва.
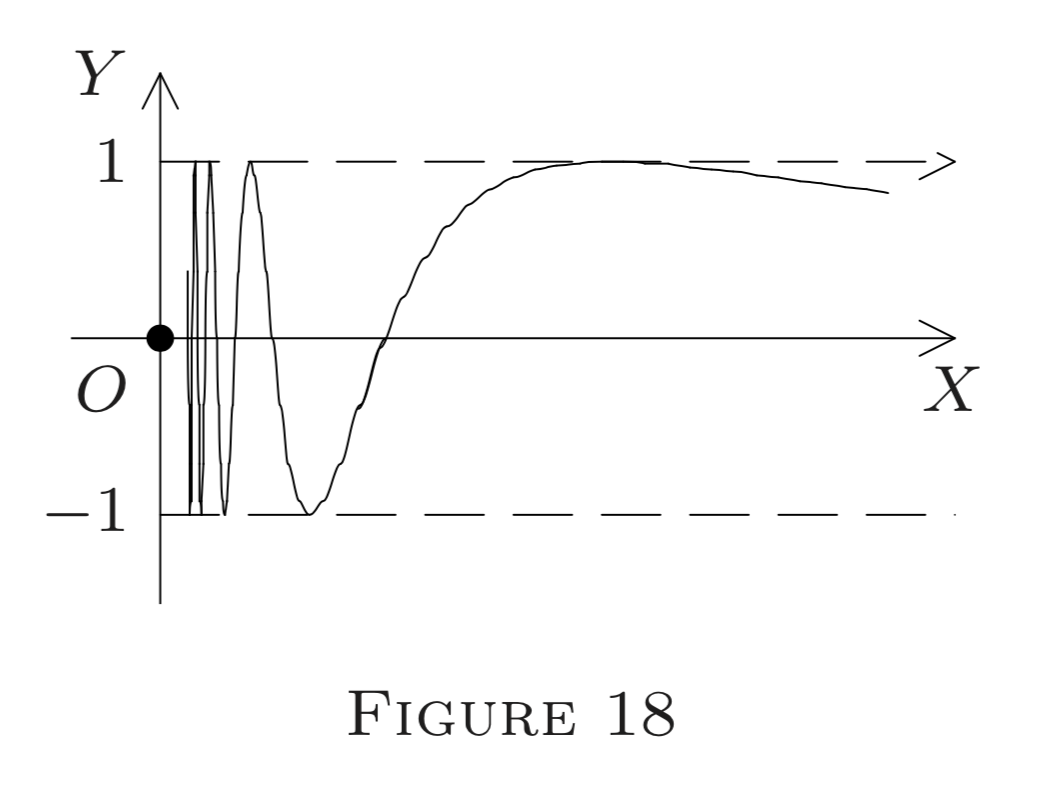
(f) Визначити\(f : E^{1} \rightarrow E^{1}\) за (див. Рис.\()\)
\[f(x)=\sin \frac{1}{x} \text{ if } x \neq 0, \text{ and } f(0)=0.\]
Будь-який глобус\(G_{0}(\delta)\) близько 0 містить точки, в яких, а\(f(x)=1,\) також ті, в яких\(f(x)=-1\) або\(f(x)=0\) (взяти\(x=2 /(n \pi)\) для великих цілих чисел\(n )\); насправді, графік «коливається» нескінченно багато разів між\(-1\) і\(1 .\) Таким чином, тим самим аргументом, що і в не\((\mathrm{c}), f\) має межа в 0 (навіть не лівий або правий межа) і, отже, переривається при\(0 .\) Жодна спроба перевизначення\(f\) при 0 не може відновити навіть ліву або праву безперервність, не кажучи вже про звичайну безперервність, при\(0 .\)
(g) Визначити\(f : E^{2} \rightarrow E^{1} \mathrm{by}\)
\[f(\overline{0})=0 \text{ and } f(\overline{x})=\frac{x_{1} x_{2}}{x_{1}^{2}+x_{2}^{2}} \text{ if } \overline{x}=\left(x_{1}, x_{2}\right) \neq \overline{0}.\]
\(B\)Дозволяти будь-який рядок\(E^{2}\) через\(\overline{0},\) заданий параметрично
\[\overline{x}=t \vec{u}, \quad t \in E^{1}, \vec{u} \text{ fixed (see Chapter 3, §§4-6 ),}\]
так\(x_{1}=t u_{1}\) і\(x_{2}=t u_{2} .\) як легко видно, для\(\overline{x} \in B, f(\overline{x})=f(\overline{u})\) (постійний) якщо\(\overline{x} \neq \overline{0} .\) Звідси
\[\left(\forall \overline{x} \in B \cap G_{\neg \overline{0}}(\delta)\right) \quad f(\overline{x})=f(\overline{u}),\]
тобто,\(\rho(f(\overline{x}), f(\overline{u}))=0<\varepsilon,\) для будь-якого\(\varepsilon>0\) видаленого глобуса о\(\overline{0}\).
До того\(\left(2^{\prime}\right),\) часу,\(f(\overline{x}) \rightarrow f(\overline{u})\) як і\(\overline{x} \rightarrow \overline{0}\) над шляхом\(B .\) Таким чином,\(f\) має відносну\(f(\overline{u})\) межу\(\overline{0},\) над будь-якою лінією,\(\overline{x}=t \overline{u},\) але ця межа відрізняється для різних варіантів,\(\overline{u},\) тобто для різних рядків через\(\overline{0} .\) Немає звичайної межі на\(\overline{0}\) існує (чому?) ; навіть не\(f\) є відносно безперервним\(\overline{0}\) над лінією,\(\overline{x}=t \vec{u}\) якщо тільки\(f(\overline{u})=0\) (що відбувається лише в тому випадку, якщо лінія є однією з координатних осей (чому?)).
