11.2: Формули та кола відстані та середини
- Page ID
- 59815
До кінця цього розділу ви зможете:
- Використовуйте формулу відстані
- Використовуйте формулу середньої точки
- Запишіть рівняння кола в стандартному вигляді
- Графік кола
Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.
- Знайти довжину гіпотенузи прямокутного трикутника, катети якого\(12\) і\(16\) дюйми.
Якщо ви пропустили цю проблему, перегляньте приклад 2.34. - Фактор:\(x^{2}-18 x+81\).
Якщо ви пропустили цю проблему, перегляньте приклад 6.24. - Вирішіть, заповнивши квадрат:\(x^{2}-12 x-12=0\).
Якщо ви пропустили цю проблему, перегляньте приклад 9.22.
У цьому розділі ми розглянемо конічні перерізи, які зазвичай називають конічними, та їх властивості. Коніки - це криві, які виходять з площини, що перетинає подвійний конус - два конуси, розміщені точка-точка. Кожну половинку подвійного конуса називають ворсом.
Є чотири конуси: коло, парабола, еліпс і гіпербола. На наступному малюнку показано, як площина, що перетинає подвійний конус, призводить до кожної кривої.
Кожна з кривих має безліч додатків, які впливають на ваше повсякденне життя, від мобільного телефону до акустики та навігаційних систем. У цьому розділі ми розглянемо властивості кола.
Використовуйте формулу відстані
Ми використовували теорему Піфагора, щоб знайти довжини сторін прямокутного трикутника. Тут ми знову будемо використовувати цю теорему, щоб знайти відстані на прямокутній системі координат. Знайшовши відстань на прямокутній системі координат, ми можемо встановити зв'язок між геометрією конічного конуса та алгеброю, що відкриває світ можливостей для застосування.
Нашим першим кроком є розробка формули для пошуку відстаней між точками прямокутної системи координат. Ми побудуємо точки і створимо прямокутний трикутник так само, як ми робили, коли ми знайшли нахил у графіках і функціях. Потім ми зробимо це на крок далі і використовуємо теорему Піфагора, щоб знайти довжину гіпотенузи трикутника - це відстань між точками.
Використовуйте прямокутну систему координат, щоб знайти відстань між точками\((6,4)\) і\((2,1)\).
Рішення
| Помітьте дві точки. З'єднайте дві точки лінією. Намалюйте прямокутний трикутник так, ніби ви збираєтеся знайти нахил. |
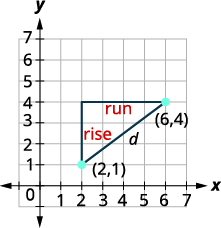
|
| Знайдіть довжину кожної ноги. |
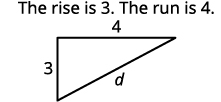
|
| Використовуйте теорему Піфагора\(d\), щоб знайти відстань між двома точками. | \(a^{2}+b^{2}=c^{2}\) |
| Підставляємо в значеннях. | \(3^{2}+4^{2}=d^{2}\) |
| Спростити. | \(9+16=d^{2}\) |
| \(25=d^{2}\) | |
| Використовуйте властивість «Квадратний корінь». | \(d=5\quad\cancel{d=-5}\) |
| Оскільки відстань,\(d\) є позитивною, ми можемо усунути\(d=-5\). | Відстань між точками\((6,4)\) і\((2,1)\) є\(5\). |
Використовуйте прямокутну систему координат, щоб знайти відстань між точками\((6,1)\) і\((2,-2)\).
- Відповідь
-
\(d=5\)
Використовуйте прямокутну систему координат, щоб знайти відстань між точками\((5,3)\) і\((-3,-3)\).
- Відповідь
-
\(d=10\)
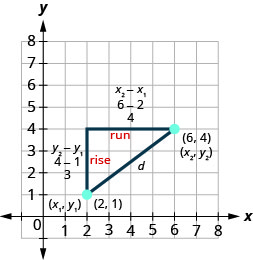
Метод, який ми використовували в останньому прикладі, призводить нас до формули, щоб знайти відстань між двома точками\(\left(x_{1}, y_{1}\right)\) і\(\left(x_{2}, y_{2}\right)\).
Коли ми знайшли довжину горизонтальної ноги, ми віднімаємо\(6−2\) яка є\(x_{2}-x_{1}\).
Коли ми знайшли довжину вертикальної ноги, ми віднімаємо\(4−1\) яка є\(y_{2}-y_{1}\).
Якщо трикутник був у іншому положенні, ми, можливо, віднімали\(x_{1}-x_{2}\) або\(y_{1}-y_{2}\). Вирази\(x_{2}-x_{1}\) і\(x_{1}-x_{2}\) варіюються тільки в знак отриманого числа. Щоб отримати позитивне значення - оскільки відстань позитивна - ми можемо використовувати абсолютне значення. Так що узагальнити скажемо\(\left|x_{2}-x_{1}\right|\) і\(\left|y_{2}-y_{1}\right|\).
У теоремі Піфагора підставляємо загальні вирази,\(\left|x_{2}-x_{1}\right|\)\(\left|y_{2}-y_{1}\right|\) а не числа.
\(\begin{array}{l c}{} & {a^{2}+b^{2}=c^{2}} \\ {\text {Substitute in the values. }}&{(|x_{2}-x_{1}|)^{2}+(|y_{2}-y_{1}|)^{2}=d^{2}} \\ {\text{Squaring the expressions makes}}&{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}=d^{2}} \\ \text{them positive, so we eliminate} \\\text{the absolute value bars.}\\ {\text{Use the Square Root Property.}}&{d=\pm\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}\\ {\text{Distance is positive, so eliminate}}&{d=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}\\\text{the negative value.}\end{array}\)
Це формула відстані, яку ми використовуємо, щоб знайти відстань\(d\) між двома точками\((x_{1},y_{1})\) і\((x_{2}, y_{2})\).
Формула відстані
Відстань\(d\) між двома точками\((x_{1},y_{1})\) і\((x_{2}, y_{2})\)
\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
Використовуйте формулу відстані, щоб знайти відстань між точками\((-5,-3)\) і\((7,2)\).
Рішення:
Напишіть формулу відстані.
\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
Позначте точки\(\left( \begin{array}{c}{x_{1}, y_{1}} \\ {-5,-3}\end{array}\right)\),\(\left( \begin{array}{l}{x_{2}, y_{2}} \\ {7,2}\end{array}\right)\) і підставляйте.
\(d=\sqrt{(7-(-5))^{2}+(2-(-3))^{2}}\)
Спростити.
\(d=\sqrt{12^{2}+5^{2}}\)
\(d=\sqrt{144+25}\)
\(d=\sqrt{169}\)
\(d=13\)
Відповідь:
\(d=13\)
Використовуйте формулу відстані, щоб знайти відстань між точками\((-4,-5)\) і\((5,7)\).
- Відповідь
-
\(d=15\)
Використовуйте формулу відстані, щоб знайти відстань між точками\((-2,-5)\) і\((-14,-10)\).
- Відповідь
-
\(d=13\)
Використовуйте формулу відстані, щоб знайти відстань між точками\((10,−4)\) і\((−1,5)\). Напишіть відповідь у точному вигляді, а потім знайдіть десяткове наближення, округлене до найближчої десятої, якщо потрібно.
Рішення:
Напишіть формулу відстані.
\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
Позначте точки\(\left( \begin{array}{c}{x_{1}, y_{1}} \\ {10,-4}\end{array}\right)\),\(\left( \begin{array}{c}{x_{2}, y_{2}} \\ {-1,5}\end{array}\right)\) і підставляйте.
\(d=\sqrt{(-1-10)^{2}+(5-(-4))^{2}}\)
Спростити.
\(d=\sqrt{(-11)^{2}+9^{2}}\)
\(d=\sqrt{121+81}\)
\(d=\sqrt{202}\)
Оскільки\(202\) це не ідеальний квадрат, ми можемо залишити відповідь у точному вигляді або знайти десяткове наближення.
\(d=\sqrt{202}\)
або
\(d \approx 14.2\)
Використовуйте формулу відстані, щоб знайти відстань між точками\((−4,−5)\) і\((3,4)\). Напишіть відповідь у точному вигляді, а потім знайдіть десяткове наближення, округлене до найближчої десятої, якщо потрібно.
- Відповідь
-
\(d=\sqrt{130}, d \approx 11.4\)
Використовуйте формулу відстані, щоб знайти відстань між точками\((−2,−5)\) і\((−3,−4)\). Напишіть відповідь у точному вигляді, а потім знайдіть десяткове наближення, округлене до найближчої десятої, якщо потрібно.
- Відповідь
-
\(d=\sqrt{2}, d \approx 1.4\)
Використовуйте формулу середньої точки
Часто корисно мати можливість знайти середню точку сегмента. Наприклад, якщо у вас є кінцеві точки діаметра кола, ви можете знайти центр кола, який є середньою точкою діаметра. Щоб знайти середню точку відрізка лінії, ми знаходимо середнє значення\(x\) -координат та середнє значення\(y\) -координат кінцевих точок.
Формула середньої точки
Середина відрізка лінії, кінцевими точками якого є дві точки\(\left(x_{1}, y_{1}\right)\) і\(\left(x_{2}, y_{2}\right)\)
\(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)
Щоб знайти середню точку відрізка лінії, ми знаходимо середнє значення\(x\) -координат та середнє значення\(y\) -координат кінцевих точок.
Скористайтеся формулою середньої точки, щоб знайти середину відрізків ліній, кінцевими точками яких є\((−5,−4)\) і\((7,2)\). Покладіть кінцеві точки та середину на прямокутній системі координат.
Рішення:
| Напишіть формулу середньої точки. | \(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\) |
| Позначте точки,\(\left( \begin{array}{c}{x_{1}, y_{1}} \\ {-5,-4}\end{array}\right), \left( \begin{array}{l}{x_{2}, y_{2}} \\ {7,2}\end{array}\right)\) і підставляйте. | \(\left(\frac{-5+7}{2}, \frac{-4+2}{2}\right)\) |
| Спростити. | \(\left(\frac{2}{2}, \frac{-2}{2}\right)\) |
|
\((1,-1)\) Середина відрізка - це точка \((1,-1)\). |
|
| Побудуйте кінцеві та середні точки. |
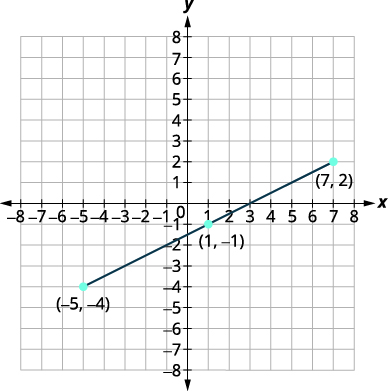
|
Скористайтеся формулою середньої точки, щоб знайти середину відрізків ліній, кінцевими точками яких є\((−3,−5)\) і\((5,7)\). Покладіть кінцеві точки та середину на прямокутній системі координат.
- Відповідь
-
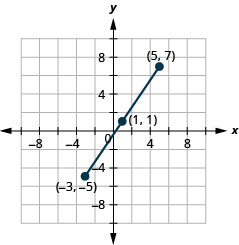
Малюнок 11.1.7
Скористайтеся формулою середньої точки, щоб знайти середину відрізків ліній, кінцевими точками яких є\((−2,−5)\) і\((6,−1)\). Покладіть кінцеві точки та середину на прямокутній системі координат.
- Відповідь
-
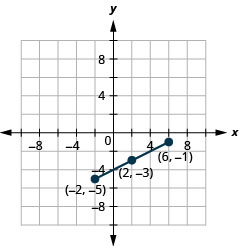
Малюнок 11.1.8
Як формула відстані, так і формула середньої точки залежать від двох точок,\(\left(x_{1}, y_{1}\right)\) і\(\left(x_{2}, y_{2}\right)\). Легко переплутати, яка формула вимагає додавання, а яка віднімання координат. Якщо ми пам'ятаємо, звідки беруться формули, може бути простіше запам'ятати формули.
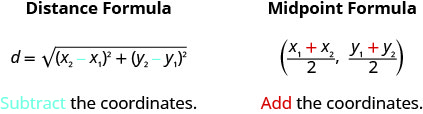
Запишіть рівняння кола в стандартній формі
Як ми вже згадували, наша мета полягає в тому, щоб з'єднати геометрію конічного конуса з алгеброю. Використовуючи координатну площину, ми можемо зробити це легко.
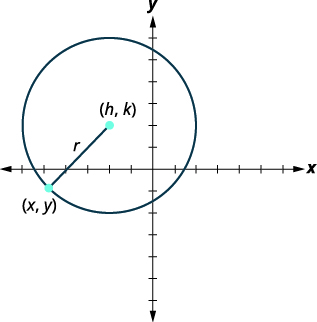
Ми визначаємо коло як усі точки на площині, які є фіксованою відстанню від заданої точки в площині. Задана точка називається центром\((h,k)\), а фіксована відстань називається \(r\)радіусом кола.
Коло - це всі точки на площині, які є фіксованою відстанню від заданої точки в площині. Задана точка називається центром\((h,k)\), а фіксована відстань називається \(r\)радіусом кола.
Дивимося на коло в прямокутній системі координат. Радіус - це відстань від центру\((h,k)\),, до точки на колі,\((x,y)\). |
|
| Щоб вивести рівняння кола, ми можемо використовувати формулу відстані з точками\((h,k)\),\((x,y)\) і відстань,\(r\). |
\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\) |
| Підставляємо значення. | \(r=\sqrt{(x-h)^{2}+(y-k)^{2}}\) |
| Квадрат з обох сторін. | \(r^{2}=(x-h)^{2}+(y-k)^{2}\) |
Це стандартна форма рівняння кола з центром\((h,k)\), і радіусом,\(r\).
Стандартна форма рівняння кола з центром\((h,k)\), і радіусом\(r\),
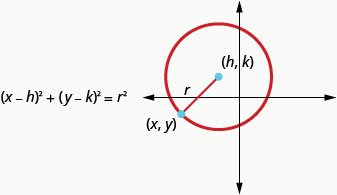
Запишіть стандартну форму рівняння кола з радіусом\(3\) і центром\((0,0)\).
Рішення:
| Використовуйте стандартну форму рівняння кола | \((x-h)^{2}+(y-k)^{2}=r^{2}\) |
| Підставляємо в значення\(r=3, h=0\), і\(k=0\). | \((x-0)^{2}+(y-0)^{2}=3^{2}\) |
 |
|
| Спростити. | \(x^{2}+y^{2}=9\) |
Запишіть стандартну форму рівняння кола з радіусом\(6\) і центром\((0,0)\).
- Відповідь
-
\(x^{2}+y^{2}=36\)
Запишіть стандартну форму рівняння кола з радіусом\(8\) і центром\((0,0)\).
- Відповідь
-
\(x^{2}+y^{2}=64\)
В останньому прикладі центр був\((0,0)\). Зверніть увагу, що сталося з рівнянням. Всякий раз\((0,0)\), коли центр є, стандартна форма стає\(x^{2}+y^{2}=r^{2}\).
Запишіть стандартну форму рівняння кола з радіусом\(2\) і центром\((−1,3)\).
Рішення:
| Використовуйте стандартну форму рівняння кола. | \((x-h)^{2}+(y-k)^{2}=r^{2}\) |
| Підставляємо в значеннях. | \((x-(-1))^{2}+(y-3)^{2}=2^{2}\) |
 |
|
| Спростити. | \((x+1)^{2}+(y-3)^{2}=4\) |
Запишіть стандартну форму рівняння кола з радіусом\(7\) і центром\((2,−4)\).
- Відповідь
-
\((x-2)^{2}+(y+4)^{2}=49\)
Запишіть стандартну форму рівняння кола з радіусом\(9\) і центром\((−3,−5)\).
- Відповідь
-
\((x+3)^{2}+(y+5)^{2}=81\)
У наступному прикладі радіус не задано. Для обчислення радіуса використовуємо формулу відстані з двома заданими точками.
Запишіть стандартну форму рівняння кола з центром\((2,4)\), який також містить точку\((−2,1)\).
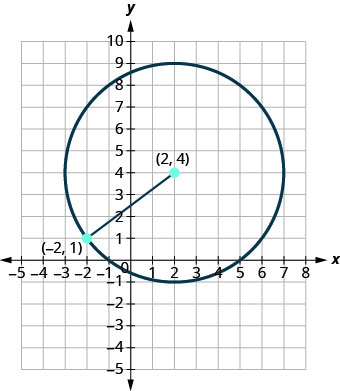
Рішення:
Радіус - це відстань від центру до будь-якої точки на колі, тому ми можемо використовувати формулу відстані для її обчислення. Ми будемо використовувати центр\((2,4)\) і точку\((−2,1)\)
Використовуйте формулу відстані, щоб знайти радіус.
\(r=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
Підставляємо значення. \(\left( \begin{array}{l}{x_{1}, y_{1}} \\ {2,4}\end{array}\right), \left( \begin{array}{c}{x_{2}, y_{2}} \\ {-2,1}\end{array}\right)\)
\(r=\sqrt{(-2-2)^{2}+(1-4)^{2}}\)
Спростити.
\(r=\sqrt{(-4)^{2}+(-3)^{2}}\)
\(r=\sqrt{16+9}\)
\(r=\sqrt{25}\)
\(r=5\)
Тепер, коли ми знаємо радіус і центр\((2,4)\), ми можемо використовувати стандартну форму рівняння кола, щоб знайти рівняння.\(r=5\)
Використовуйте стандартну форму рівняння кола.
\((x-h)^{2}+(y-k)^{2}=r^{2}\)
Підставляємо в значеннях.
\((x-2)^{2}+(y-4)^{2}=5^{2}\)
Спростити.
\((x-2)^{2}+(y-4)^{2}=25\)
Запишіть стандартну форму рівняння кола з центром\((2,1)\), який також містить точку\((−2,−2)\).
- Відповідь
-
\((x-2)^{2}+(y-1)^{2}=25\)
Запишіть стандартну форму рівняння кола з центром\((7,1)\), який також містить точку\((−1,−5)\).
- Відповідь
-
\((x-7)^{2}+(y-1)^{2}=100\)
Графік кола
Будь-яке рівняння виду\((x-h)^{2}+(y-k)^{2}=r^{2}\) є стандартною формою рівняння кола з центром\((h,k)\), і радіусом,\(r\). Потім ми можемо намалювати коло на прямокутній системі координат.
Зверніть увагу, що стандартна форма вимагає віднімання з\(x\) і\(y\). У наступному прикладі рівняння має\(x+2\), тому нам потрібно переписати додавання як віднімання негативу.
Знайдіть центр і радіус, потім намалюйте графік кола:\((x+2)^{2}+(y-1)^{2}=9\).
Рішення:
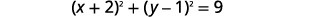 |
|
|
Використовуйте стандартну форму рівняння кола. Визначте центр,\((h,k)\) і радіус,\(r\). |
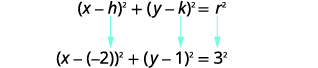 |
| Центр:\((-2,1)\) радіус:\(3\) | |
| Графік кола. | 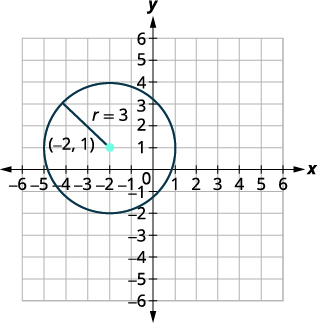 |
- Знайдіть центр і радіус, потім
- Графік кола:\((x-3)^{2}+(y+4)^{2}=4\).
- Відповідь
-
- Коло по центру\((3,-4)\) з радіусом\(2\).
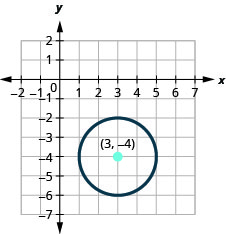
Малюнок 11.1.19
- Знайдіть центр і радіус, потім
- Графік кола:\((x-3)^{2}+(y-1)^{2}=16\).
- Відповідь
-
- Коло по центру\((3,1)\) з радіусом\(4\).
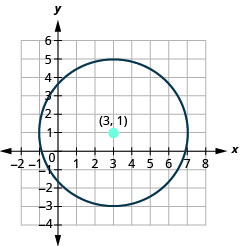
Малюнок 11.1.20
Щоб знайти центр і радіус, ми повинні написати рівняння в стандартному вигляді. У наступному прикладі ми повинні спочатку отримати коефіцієнт\(x^{2}, y^{2}\) бути одиницею.
Знайдіть центр і радіус, а потім графік кола,\(4 x^{2}+4 y^{2}=64\).
Рішення:
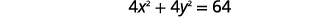 |
|
| Розділіть кожну сторону на\(4\). | 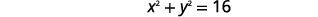 |
| Використовуйте стандартну форму рівняння кола. Визначте центр,\((h,k)\) і радіус,\(r\). |
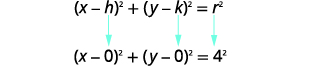 |
| Центр:\((0,0)\) радіус:\(4\) | |
| Графік кола. | 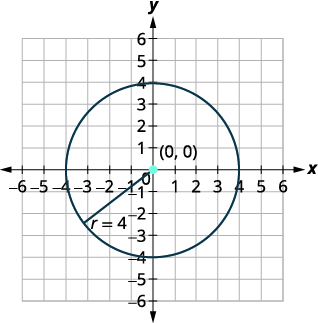 |
- Знайдіть центр і радіус, потім
- Графік кола:\(3 x^{2}+3 y^{2}=27\)
- Відповідь
-
- Коло по центру\((0,0)\) з радіусом\(3\).
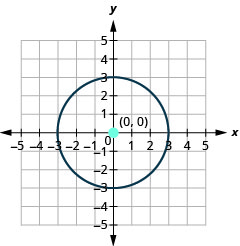
Малюнок 11.1.25
- Знайдіть центр і радіус, потім
- Графік кола:\(5 x^{2}+5 y^{2}=125\)
- Відповідь
-
- Коло по центру\((0,0)\) з радіусом\(5\).
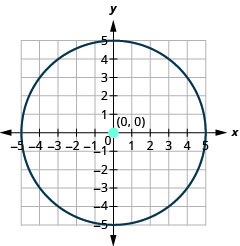
Малюнок 11.1.26
Якщо розгорнути рівняння з прикладу 11.1.8\((x+2)^{2}+(y-1)^{2}=9\), рівняння кола виглядає зовсім інакше.
\((x+2)^{2}+(y-1)^{2}=9\)
Квадратні двочлени.
\(x^{2}+4 x+4+y^{2}-2 y+1=9\)
Впорядкуйте терміни в порядку зменшення ступеня, і отримайте нуль праворуч
\(x^{2}+y^{2}+4 x-2 y-4=0\)
Така форма рівняння називається загальною формою рівняння кола.
Загальна форма рівняння кола дорівнює
\(x^{2}+y^{2}+a x+b y+c=0\)
Якщо нам дано рівняння в загальному вигляді, ми можемо змінити його на стандартну форму, заповнивши квадрати в обох\(x\) і\(y\). Тоді ми можемо намалювати коло, використовуючи його центр і радіус.
- Знайдіть центр і радіус, потім
- Графік кола:\(x^{2}+y^{2}-4 x-6 y+4=0\)
Рішення:
Нам потрібно переписати цю загальну форму в стандартну форму, щоб знайти центр і радіус.
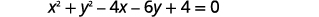
|
|
| Згрупуйте\(x\) -терміни і\(y\) -терміни. Зберіть константи з правого боку. |
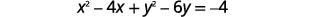
|
| Завершіть квадрати. |
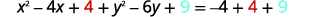
|
| Перепишіть як біноміальні квадрати. |
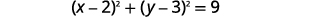
|
| Визначте центр і радіус. | Центр:\((2,3)\) радіус:\(3\) |
| Графік кола. |
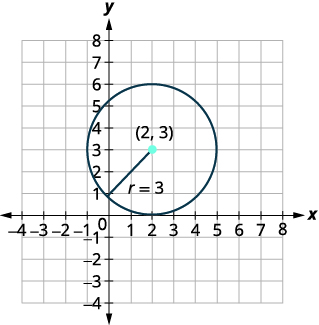
|
- Знайдіть центр і радіус, потім
- Графік кола:\(x^{2}+y^{2}-6 x-8 y+9=0\).
- Відповідь
-
- Коло по центру\((3,4)\) з радіусом\(4\).
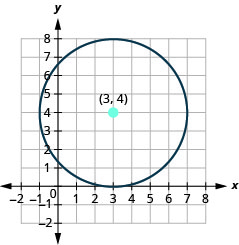
Малюнок 11.1.32
- Знайдіть центр і радіус, потім
- Графік кола:\(x^{2}+y^{2}+6 x-2 y+1=0\)
- Відповідь
-
- Коло по центру\((-3,1)\) з радіусом\(3\).
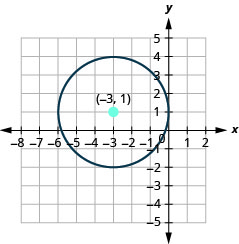
Малюнок 11.1.33
У наступному прикладі є\(y\) -термін і a\(y^{2}\) -термін. Але зверніть увагу, що немає\(x\) -термін, тільки\(x^{2}\) -термін. Ми бачили це раніше і знаємо, що\(h\) це означає\(0\). Нам потрібно буде заповнити квадрат для\(y\) термінів, але не для\(x\) термінів.
- Знайдіть центр і радіус, потім
- Графік кола:\(x^{2}+y^{2}+8 y=0\)
Рішення:
Нам потрібно переписати цю загальну форму в стандартну форму, щоб знайти центр і радіус.
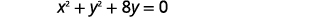 |
|
| Згрупуйте\(x\) -терміни і\(y\) -терміни. | 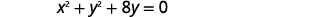 |
| Немає констант для збору з правого боку. | |
| Завершіть квадрат для\(y^{2}+8y\). | 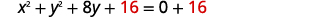 |
| Перепишіть як біноміальні квадрати. | 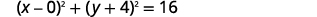 |
| Визначте центр і радіус. | Центр:\((0,-4)\) радіус:\(4\) |
| Графік кола. | 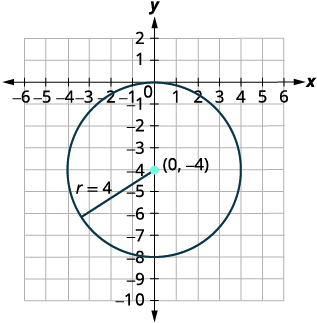 |
- Знайдіть центр і радіус, потім
- Графік кола:\(x^{2}+y^{2}-2 x-3=0\).
- Відповідь
-
- Коло по центру\((-1,0)\) з радіусом\(2\).
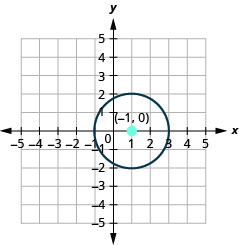
Малюнок 11.1.39
- Знайдіть центр і радіус, потім
- Графік кола:\(x^{2}+y^{2}-12 y+11=0\).
- Відповідь
-
- Коло по центру\((0,6)\) з радіусом\(5\).
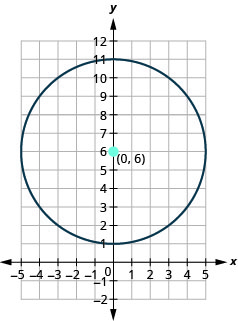
Малюнок 11.1.40
Отримайте доступ до цих онлайн-ресурсів для отримання додаткових інструкцій та практики за допомогою формул відстані та середньої точки та графічних кіл.
- Формули та кола відстань-середина
- Пошук відстані та середини між двома точками
- Завершення квадрата для написання рівняння у стандартній формі кола
Ключові концепції
- Відстань формула: відстань\(d\) між двома точками\(\left(x_{1}, y_{1}\right)\) і\(\left(x_{2}, y_{2}\right)\)
\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
- середина формули: середина відрізка лінії, кінцеві точки якої дві точки\(\left(x_{1}, y_{1}\right)\) і\(\left(x_{2}, y_{2}\right)\)
\(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)
Щоб знайти середню точку відрізка лінії, ми знаходимо середнє значення\(x\) -координат та середнє значення\(y\) -координат кінцевих точок. - Коло: Коло - це всі точки на площині, які є фіксованою відстанню від фіксованої точки на площині. Задана точка називається центром\((h,k)\), а фіксована відстань називається \(r\)радіусом кола.
- Стандартна форма рівняння кола: стандартна форма рівняння кола з центром\((h,k)\), і радіусом\(r\)
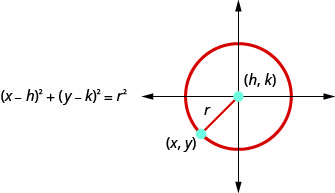
- Загальна форма рівняння кола: загальна форма рівняння кола
\(x^{2}+y^{2}+a x+b y+c=0\)
Глосарій
- коло
- Коло - це всі точки в площині, які є фіксованою відстанню від фіксованої точки в площині.
