9.9: Вирішити квадратичні нерівності

Last updated
Save as PDF

Page ID: 59682

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

До кінця цього розділу ви зможете:

Розв'язувати квадратичні нерівності графічно
Розв'язувати квадратичні нерівності алгебраїчно

Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.

Вирішити:$2x−3=0$.
Якщо ви пропустили цю проблему, перегляньте приклад 2.2.
Вирішити:$2y^{2}+y=15$.
Якщо ви пропустили цю проблему, перегляньте приклад 6.45.
Вирішити$\frac{1}{x^{2}+2 x-8}>0$
Якщо ви пропустили цю проблему, перегляньте приклад 7.56.

Раніше ми навчилися вирішувати лінійні нерівності та раціональні нерівності. Деякі методи, які ми використовували для їх вирішення, були однаковими, а деякі - різними. Зараз ми навчимося вирішувати нерівності, які мають квадратичний вираз. Ми будемо використовувати деякі методи розв'язування лінійних і раціональних нерівностей, а також квадратичні рівняння. Розв'яжемо квадратичні нерівності двома шляхами — графічно і алгебраїчно.

Розв'язувати квадратичні нерівності графічно

Квадратне рівняння знаходиться в стандартній формі, коли записано як$ax^{2}+bx+c=0$. Якщо замінити знак рівності знаком нерівності, то маємо квадратичну нерівність в стандартній формі.

Визначення$\PageIndex{1}$: Quadratic Inequality

Квадратична нерівність - це нерівність, яка містить квадратичний вираз. Записується стандартна форма квадратичної нерівності:

$\begin{array}{ll}{a x^{2}+b x+c<0} & {a x^{2}+b x+c \leq 0} \\ {a x^{2}+b x+c>0} & {a x^{2}+b x+c \geq 0}\end{array}$

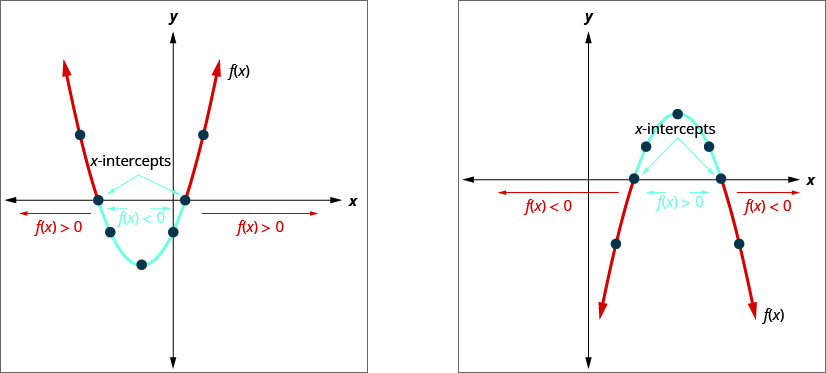
Графік квадратичної функції$f(x)=a x^{2}+b x+c=0$ - парабола. Коли ми запитуємо, коли є$a x^{2}+b x+c<0$, ми запитуємо, коли є$f(x)<0$. Ми хочемо знати, коли парабола знаходиться нижче$x$ -осі.

Коли ми запитуємо, коли є$a x^{2}+b x+c>0$, ми запитуємо, коли є$f(x)>0$. Ми хочемо знати, коли парабола знаходиться над$y$ -віссю.

Перший графік - це парабола, звернена вгору, f або x, на координатній площині x y. Ліворуч від функції f з x більше 0. Між x-перехопленнями f з x менше 0. Праворуч від функції f з x більше 0. Другий графік - це парабола, спрямована вниз, f або x, на координатній площині x y. Ліворуч від функції f з x менше 0. Між x-перехопленнями f з x більше 0. Праворуч від функції f з x менше 0. — Малюнок 9.8.1

Приклад$\PageIndex{1}$: How to Solve a Quadratic Inequality Graphically

$x^{2}−6x+8<0$Вирішуйте графічно. Запишіть рішення в інтервальних позначеннях.

Рішення:

Крок 1: Запишіть квадратичну нерівність у стандартній формі.

Нерівність знаходиться в стандартній формі.

$x^{2}-6 x+8<0$

Крок 2: Графік функції за$f(x)=a x^{2}+b x+c$ допомогою властивостей або перетворень.

Ми будемо графувати, використовуючи властивості.

$f(x)=x^{2}-6 x+8$

Подивіться$a$ на рівняння.

$\color{red}{a=1, b=-6, c=8}$

$f(x)=x^{2}-6 x+8$

$a$Оскільки позитивна, парабола відкривається вгору.

Парабола відкривається вгору.

$f(x)=x^{2}-6 x+8$

Віссю симетрії є лінія$x=-\frac{b}{2 a}$.

Вісь симетрії

$x=-\frac{b}{2 a}$

$\begin{array}{l}{x=-\frac{(-6)}{2 \cdot 1}} \\ {x=3}\end{array}$

Віссю симетрії є лінія$x=3$.

Вершина знаходиться на осі симетрії. $x=3$Підставляємо в функцію.

Вершина

$\begin{array}{l}{f(x)=x^{2}-6 x+8} \\ {f(3)=(\color{red}{3}\color{black}{)}^{2}-6(\color{red}{3}\color{black}{)}+8} \\ {f(3)=-1}\end{array}$

Вершина є$(3,-1)$.

знаходимо$f(0)$

$y$-перехопити

$\begin{array}{l}{f(x)=x^{2}-6 x+8} \\ {f(0)=(\color{red}{0}\color{black}{)}^{2}-6(\color{red}{0}\color{black}{)}+8} \\ {f(0)=8}\end{array}$

$y$-Перехоплення є$(0.8)$.

Використовуємо вісь симетрії, щоб знайти точку, симетричну$y$ -перехоплення. $y$-Перехоплення - це$3$ одиниці зліва від осі симетрії,$x=3$. Точка$3$ одиниць праворуч від осі симетрії має$x=6$.

Точка симетрична до$y$ -перехоплення

Справа в тому$(6,8)$.

Вирішуємо$f(x)=0$.

$x$-перехоплює

Ми можемо вирішити це квадратне рівняння шляхом факторингу.

$\begin{aligned} f(x) &=x^{2}-6 x+8 \\ \color{red}{0} &\color{black}{=}x^{2}-6 x+8 \\ \color{red}{0} &\color{black}{=}(x-2)(x-4) \\ x &=2 \text { or } x=4 \end{aligned}$

$x$-перехоплює є$(2,0)$ і$(4,0)$.

Ми графуємо вершину, перехоплює і точку симетричну до$y$ -перехоплення. З'єднуємо ці$5$ точки, щоб накидати параболу.

Крок 3: Визначте рішення з графіка.

$x^{2}-6 x+8<0$

Нерівність запитує значення$x$, які роблять функцію меншою, ніж$0$. Які значення$x$ роблять параболу нижче$x$ -осі.

Ми не включаємо цінності$2$,$4$ так як нерівність менше, ніж тільки.

Рішення, в інтервальних позначеннях, є$(2,4)$.

Вправа$\PageIndex{1}$

$x^{2}+2 x-8<0$Вирішуйте графічно
Запишіть рішення в інтервальних позначеннях

Відповідь

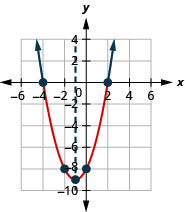
$На цьому малюнку показана парабола, що відкривається вгору, на координатній площині x y. Він має вершину (від'ємний 2, від'ємний 9), y-перехоплення (0, 8), а вісь симетрії показана при x дорівнює негативному 2.$
Малюнок 9.8.4
$(-4,2)$

Вправа$\PageIndex{2}$

$x^{2}-8 x+12 \geq 0$Вирішуйте графічно
Запишіть рішення в інтервальних позначеннях

Відповідь

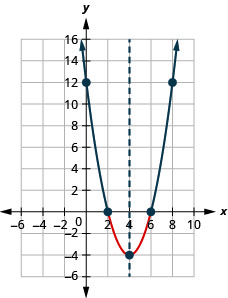
$На цьому малюнку показана парабола, що відкривається вгору, на координатній площині x y. Він має вершину (4, від'ємний 4) та x-перехоплення (2, 0) та (6, 0).$
Малюнок 9.8.5
$(-\infty, 2] \cup[6, \infty)$

Перерахуємо кроки, які потрібно зробити для графічного розв'язання квадратичної нерівності.

Розв'язувати квадратичну нерівність графічно

Запишіть квадратичну нерівність в стандартній формі.
Графік функції$f(x)=ax^{2}+bx+c$.
Визначте рішення по графіку.

В останньому прикладі парабола відкрилася вгору і в наступному прикладі відкривається вниз. В обох випадках ми шукаємо частину параболи, яка знаходиться нижче$x$ -осі, але зауважте, як положення параболи впливає на рішення.

Приклад$\PageIndex{2}$

$-x^{2}-8 x-12 \leq 0$Вирішуйте графічно. Запишіть рішення в інтервальних позначеннях.

Рішення:

Таблиця 9.8.1
Квадратична нерівність у стандартній формі.	$-x^{2}-8 x-12 \leq 0$
Графік функції $f(x)=-x^{2}-8 x-12$	Парабола відкривається вниз. $.$ Малюнок 9.8.6
Знайдіть лінію симетрії.	$\begin{array}{l}{x=-\frac{b}{2 a}} \\ {x=-\frac{-8}{2(-1)}} \\ {x=-4}\end{array}$
Знайдіть вершину.	$\begin{aligned} f(x) &=-x^{2}-8 x-12 \\ f(-4) &=-(-4)^{2}-8(-4)-12 \\ f(-4) &=-16+32-12 \\ & f(-4)=4 \end{aligned}$ Вершина$(-4,4)$
Знайдіть$x$ -перехоплення. Нехай$f(x)=0$.	$\begin{aligned} f(x) &=-x^{2}-8 x-12 \\ 0 &=-x^{2}-8 x-12 \end{aligned}$
Фактор: Використовуйте властивість нульового продукту.	$\begin{array}{l}{0=-1(x+6)(x+2)} \\ {x=-6 \quad x=-2}\end{array}$
Графік параболи.	$x$-перехоплює$(-6,0), (-2.0)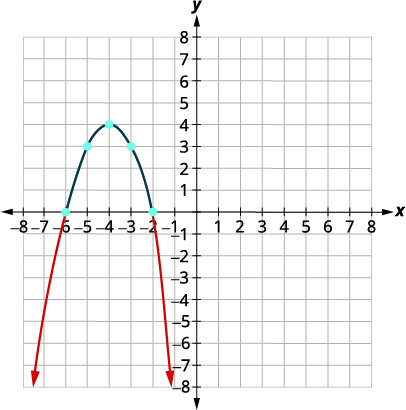$ $.$ Малюнок 9.8.7
Визначте рішення по графіку. Ми включаємо$x$ -перехоплення, оскільки нерівність «менше або дорівнює».	$(-\infty,-6] \cup[-2, \infty)$

Вправа$\PageIndex{3}$

$-x^{2}-6 x-5>0$Вирішуйте графічно
Запишіть рішення в інтервальних позначеннях

Відповідь

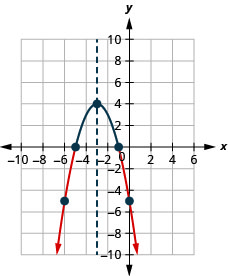
$Парабола, спрямована вниз, на координатній площині x y. Він має вершину (від'ємний 3, 4), y-перехоплення в (0, від'ємний 5), а вісь симетрії, показана при x, дорівнює негативному 3.$
Малюнок 9.8.8
$(-5,-1)$

Вправа$\PageIndex{4}$

$−x^{2}+10x−16≤0$Вирішуйте графічно
Запишіть рішення в інтервальних позначеннях

Відповідь

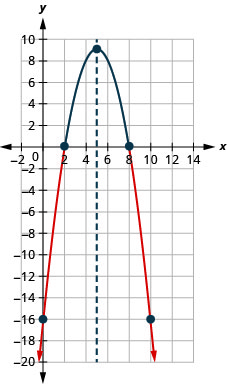
$Парабола, спрямована вниз, на координатній площині x y. Він має вершину (5, 9), y-перехоплення в (0, від'ємний 16), а вісь симетрії x дорівнює 5.$
Малюнок 9.8.9
$(-\infty, 2] \cup[8, \infty)$

Алгебраїчно розв'язувати квадратичні нерівності

Алгебраїчний метод, який ми будемо використовувати, дуже схожий на метод, який ми використовували для вирішення раціональних нерівностей. Ми знайдемо критичні точки для нерівності, які будуть розв'язками пов'язаного квадратного рівняння. Запам'ятати поліноміальний вираз можна змінювати знаки тільки там, де вираз дорівнює нулю.

Ми будемо використовувати критичні точки, щоб розділити числову лінію на інтервали, а потім визначити, чи буде квадратичний вираз позитивним або негативним в інтервалі. Потім ми визначаємо рішення для нерівності.

Приклад$\PageIndex{3}$: How to Solve Quadratic Inequalities Algebraically

Вирішити$x^{2}-x-12 \geq 0$ алгебраїчно. Запишіть рішення в інтервальних позначеннях.

Рішення:

Таблиця 9.8.2
Крок 1: Запишіть квадратичну нерівність у стандартній формі.	Нерівність знаходиться в стандартній формі.	$x^{2}-x-12 \geq 0$
Крок 2: Визначте критичні точки - рішення відповідного квадратного рівняння.	Змініть знак нерівності на знак рівності, а потім вирішіть рівняння.	$\begin{array}{c}{x^{2}-x-12=0} \\ {(x+3)(x-4)=0} \\ {x+3=0 \quad x-4=0} \\ {x=-3 \quad x=4}\end{array}$
Крок 3: Використовуйте критичні точки, щоб розділити числову лінію на інтервали.	$4$Використовувати$-3$ і розділити числову лінію на інтервали.	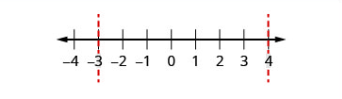$Знімок екрана (4) .png$
Крок 4: Над числовим рядком покажіть знак кожного квадратичного виразу, використовуючи контрольні точки з кожного інтервалу, заміненого вихідною нерівністю.	Тест: $x=-5$ $x=0$ $x=5$	$\begin{array}{ccc}{x^{2}-x-12} & {x^{2}-x-12} & {x^{2}-x-12} \\ {(-5)^{2}-(-5)-12} & {0^{2}-0-12} & {5^{2}-5-12} \\ {18} & {-12} & {8}\end{array}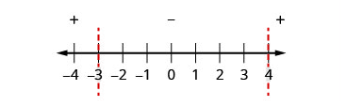$ $Знімок екрана (5) .png$ Малюнок 9.8.11
Крок 5: Визначте інтервали, де нерівність правильна. Запишіть рішення в інтервальних позначеннях.	$x^{2}-x-12 \geq 0$ Нерівність є позитивною в першому і останньому інтервалах і дорівнює$0$ в точках$-4,3$.	Рішення, в інтервальних позначеннях, є$(-\infty,-3] \cup[4, \infty)$.

Вправа$\PageIndex{5}$

Вирішити$x^{2}+2x−8≥0$ алгебраїчно. Запишіть рішення в інтервальних позначеннях.

Відповідь: $(-\infty,-4] \cup[2, \infty)$

Вправа$\PageIndex{6}$

Вирішити$x^{2}−2x−15≤0$ алгебраїчно. Запишіть рішення в інтервальних позначеннях.

Відповідь: $[-3,5]$

У цьому прикладі, оскільки$x^{2}−x−12$ фактори виразу приємно, ми також можемо знайти знак у кожному інтервалі так само, як ми робили, коли ми вирішували раціональні нерівності. Знаходимо ознаку кожного з факторів, а потім і ознака продукту. Наш номер рядка хотів би це:

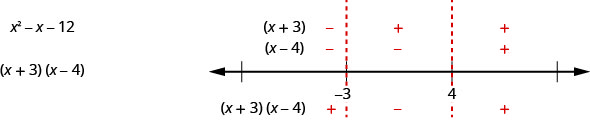
На малюнку показано вираз x у квадраті мінус х мінус 12, врахований на величину x плюс 3 рази кількість x мінус 4. На зображенні показано цифрову лінію із пунктирними лініями на від'ємних 3 і 4. Він показує ознаки кількості х плюс 3 як негативний, позитивний, позитивний, а знаки кількості х мінус 4 - негативними, негативними, позитивними. Під цифровим рядком він показує кількість х плюс 3 рази кількість х мінус 4 зі знаками позитивний, негативний, позитивний. — Малюнок 9.8.12

Результат такий же, як ми знайшли за допомогою іншого методу.

Ми підсумовуємо кроки тут.

Розв'язувати квадратичну нерівність алгебраїчно

Запишіть квадратичну нерівність в стандартній формі.
Визначте критичні точки — розв'язки відповідного квадратного рівняння.
Використовуйте критичні точки, щоб розділити числову лінію на інтервали.
Над числовим рядком показуємо знак кожного квадратичного виразу, використовуючи контрольні точки з кожного інтервалу, заміщеного у вихідну нерівність.
Визначте інтервали, де нерівність правильна. Запишіть рішення в інтервальних позначеннях.

Приклад$\PageIndex{4}$

Вирішити$x^{2}+6x−7≥0$ алгебраїчно. Запишіть рішення в інтервальних позначеннях.

Рішення:

Таблиця 9.8.3
Запишіть квадратичну нерівність в стандартній формі.	$-x^{2}+6 x-7 \geq 0$
Помножте обидві сторони нерівності на$-1$. Не забудьте змінити знак нерівності.	$x^{2}-6 x+7 \leq 0$
Визначте критичні точки, вирішивши пов'язане квадратне рівняння.	$x^{2}-6 x+7=0$
Напишіть квадратичну формулу.	$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$
Потім підставляємо в значення$a, b, c$.	$x=\frac{-(-6) \pm \sqrt{(-6)^{2}-4 \cdot 1 \cdot(7)}}{2 \cdot 1}$
Спростити.	$x=\frac{6 \pm \sqrt{8}}{2}$
Спростити радикал.	$x=\frac{6 \pm 2 \sqrt{2}}{2}$
Прибрати загальний фактор,$2$.	$\begin{array}{l}{x=\frac{2(3 \pm \sqrt{2})}{2}} \\ {x=3 \pm \sqrt{2}} \\ {x=3+\sqrt{2}} \quad x=3-\sqrt{2} \\ {x \approx 1.6}\quad\quad\:\:\: x\approx 4.4\end{array}$
Використовуйте критичні точки, щоб розділити числову лінію на інтервали. Тестові числа з кожного інтервалу в початковій нерівності.	$.$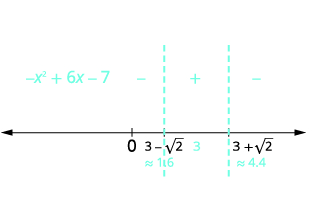
Визначте інтервали, де нерівність правильна. Запишіть рішення в інтервальних позначеннях.	$-x^{2}+6 x-7 \geq 0$в середньому проміжку$[3-\sqrt{2}, 3+\sqrt{2}]$

Вправа$\PageIndex{7}$

Вирішити$−x^{2}+2x+1≥0$ алгебраїчно. Запишіть рішення в інтервальних позначеннях.

Відповідь: $[-1-\sqrt{2},-1+\sqrt{2}]$

Вправа$\PageIndex{8}$

Вирішити$−x^{2}+8x−14<0$ алгебраїчно. Запишіть рішення в інтервальних позначеннях.

Відповідь: $(-\infty, 4-\sqrt{2}) \cup(4+\sqrt{2}, \infty)$

Розв'язки квадратичних нерівностей у кожному з попередніх прикладів були або інтервалом, або об'єднанням двох інтервалів. Це стало результатом того, що в кожному випадку ми знайшли два розв'язки відповідного квадратного рівняння$ax^{2}+bx+c=0$. Потім ці два рішення дали нам або два$x$ - перехоплення для графіка, або дві критичні точки, щоб розділити числову лінію на інтервали.

Це корелює з нашим попереднім обговоренням числа та типу розв'язків квадратного рівняння з використанням дискримінанту.

Для квадратного рівняння виду$ax^{2}+bc+c=0, a≠0$.

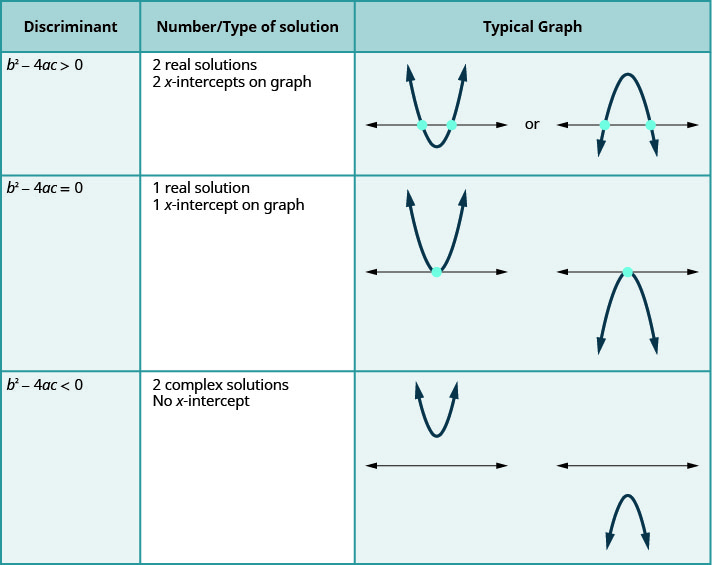
Малюнок являє собою таблицю з 3 стовпцями. Стовпець 1 позначений дискримінантним, стовпець 2 — «Число/тип рішення», а стовпець 3 — Типовий графік. Читання по стовпцях, якщо b у квадраті мінус 4 рази на c більше 0, буде 2 реальних рішення, оскільки на графіку є 2 x перехоплення. Зображення типового графіка - висхідна або низхідна парабола з 2 x-перехопленнями. Якщо дискримінант b у квадраті мінус 4 рази на c дорівнює 0, то існує 1 реальне рішення, оскільки на графіку є 1 x перехоплення. Зображення типового графіка - це парабола, спрямована вгору або вниз, яка має вершину на осі x замість перетину через неї. Якщо дискримінант b у квадраті мінус 4 рази на c менше 0, існує 2 комплексних рішення, оскільки немає перехоплення x. Зображення типового графіка показує параболу, спрямовану вгору або вниз, яка не перетинає вісь x. — Малюнок 9.8.14

Останній рядок таблиці показує нам, коли параболи ніколи не перетинають$x$ вісь -. Використовуючи квадратну формулу для розв'язання квадратного рівняння, радиканд є негативним. Отримуємо два комплексних рішення.

У наступному прикладі розв'язки квадратичної нерівності будуть результатом розв'язання комплексного квадратного рівняння.

Приклад$\PageIndex{5}$

Вирішіть, записуючи будь-яке рішення в інтервальне позначення:

$x^{2}-3 x+4>0$
$x^{2}-3 x+4 \leq 0$

Рішення:

а.

Таблиця 9.8.4
Запишіть квадратичну нерівність в стандартній формі.	$-x^{2}-3 x+4>0$
Визначте критичні точки, вирішивши пов'язане квадратне рівняння.	$x^{2}-3 x+4=0$
Напишіть квадратичну формулу.	$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$
Потім підставляємо в значення$a, b, c$.	$x=\frac{-(-3) \pm \sqrt{(-3)^{2}-4 \cdot 1 \cdot(4)}}{2 \cdot 1}$
Спростити.	$x=\frac{3 \pm \sqrt{-7}}{2}$
Спростити радиканд.	$x=\frac{3 \pm \sqrt{7 i}}{2}$
Складні рішення говорять нам, що парабола не перехоплює$x$ -вісь. Також парабола відкривається вгору. Це говорить нам про те, що парабола повністю вище$x$ -осі.	Комплексні рішення 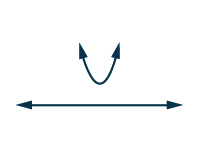$.$ Малюнок 9.8.15

Ми повинні знайти рішення для цього$x^{2}−3x+4>0$. Оскільки для всіх значень$x$ графіка знаходиться вище$x$ -осі, всі значення$x$ роблять нерівність істинною. У інтервальні позначення записуємо$(−∞,∞)$.

b. запишіть квадратичну нерівність в стандартній формі.

$x^{2}-3 x+4 \leq 0$

Визначте критичні точки, вирішивши пов'язане квадратне рівняння.

$x^{2}-3 x+4=0$

Оскільки відповідне квадратне рівняння таке ж, як і в частині (а), парабола буде такою ж. Парабола відкривається вгору і повністю знаходиться вище$x$ -осі - жодна її частина не знаходиться нижче$x$ -осі.

Ми повинні знайти рішення для цього$x^{2}−3x+4≤0$. Оскільки для всіх значень$x$ графіка ніколи не знаходиться нижче$x$ -осі, ніякі значення не$x$ роблять нерівність істинною. Рішення нерівності не існує.

Вправа$\PageIndex{9}$

Розв'яжіть і запишіть будь-яке рішення в інтервальне позначення:

$-x^{2}+2 x-4 \leq 0$
$-x^{2}+2 x-4 \geq 0$

Відповідь

$(-\infty, \infty)$
немає рішення

Вправа$\PageIndex{10}$

Розв'яжіть і запишіть будь-яке рішення в інтервальне позначення:

$x^{2}+3 x+3<0$
$x^{2}+3 x+3>0$

Відповідь

немає рішення
$(-\infty, \infty)$

Ключові поняття

Розв'язувати квадратичну нерівність графічно
1. Запишіть квадратичну нерівність в стандартній формі.
2. Графік функції за$f(x)=ax^{2}+bx+c$ допомогою властивостей або перетворень.
3. Визначте рішення по графіку.
Як розв'язати квадратичну нерівність алгебраїчно
1. Запишіть квадратичну нерівність в стандартній формі.
2. Визначте критичні точки — розв'язки відповідного квадратного рівняння.
3. Використовуйте критичні точки, щоб розділити числову лінію на інтервали.
4. Над числовим рядком показуємо знак кожного квадратичного виразу, використовуючи контрольні точки з кожного інтервалу, заміщеного у вихідну нерівність.
5. Визначте інтервали, де нерівність правильна. Запишіть рішення в інтервальних позначеннях.

Глосарій

квадратична нерівність: Квадратична нерівність - це нерівність, яка містить квадратичний вираз.

Квадратична нерівність у стандартній формі.	\(-x^{2}-8 x-12 \leq 0\)
Графік функції \(f(x)=-x^{2}-8 x-12\)	Парабола відкривається вниз. $.$ Малюнок 9.8.6
Знайдіть лінію симетрії.	\(\begin{array}{l}{x=-\frac{b}{2 a}} \\ {x=-\frac{-8}{2(-1)}} \\ {x=-4}\end{array}\)
Знайдіть вершину.	\(\begin{aligned} f(x) &=-x^{2}-8 x-12 \\ f(-4) &=-(-4)^{2}-8(-4)-12 \\ f(-4) &=-16+32-12 \\ & f(-4)=4 \end{aligned}\) Вершина\((-4,4)\)
Знайдіть\(x\) -перехоплення. Нехай\(f(x)=0\).	\(\begin{aligned} f(x) &=-x^{2}-8 x-12 \\ 0 &=-x^{2}-8 x-12 \end{aligned}\)
Фактор: Використовуйте властивість нульового продукту.	\(\begin{array}{l}{0=-1(x+6)(x+2)} \\ {x=-6 \quad x=-2}\end{array}\)
Графік параболи.	\(x\)-перехоплює\((-6,0), (-2.0)\) $.$ Малюнок 9.8.7
Визначте рішення по графіку. Ми включаємо\(x\) -перехоплення, оскільки нерівність «менше або дорівнює».	\((-\infty,-6] \cup[-2, \infty)\)

Запишіть квадратичну нерівність в стандартній формі.	\(-x^{2}+6 x-7 \geq 0\)
Помножте обидві сторони нерівності на\(-1\). Не забудьте змінити знак нерівності.	\(x^{2}-6 x+7 \leq 0\)
Визначте критичні точки, вирішивши пов'язане квадратне рівняння.	\(x^{2}-6 x+7=0\)
Напишіть квадратичну формулу.	\(x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
Потім підставляємо в значення\(a, b, c\).	\(x=\frac{-(-6) \pm \sqrt{(-6)^{2}-4 \cdot 1 \cdot(7)}}{2 \cdot 1}\)
Спростити.	\(x=\frac{6 \pm \sqrt{8}}{2}\)
Спростити радикал.	\(x=\frac{6 \pm 2 \sqrt{2}}{2}\)
Прибрати загальний фактор,\(2\).	\(\begin{array}{l}{x=\frac{2(3 \pm \sqrt{2})}{2}} \\ {x=3 \pm \sqrt{2}} \\ {x=3+\sqrt{2}} \quad x=3-\sqrt{2} \\ {x \approx 1.6}\quad\quad\:\:\: x\approx 4.4\end{array}\)
Використовуйте критичні точки, щоб розділити числову лінію на інтервали. Тестові числа з кожного інтервалу в початковій нерівності.	$.$
Визначте інтервали, де нерівність правильна. Запишіть рішення в інтервальних позначеннях.	\(-x^{2}+6 x-7 \geq 0\)в середньому проміжку\([3-\sqrt{2}, 3+\sqrt{2}]\)

Запишіть квадратичну нерівність в стандартній формі.	\(-x^{2}-3 x+4>0\)
Визначте критичні точки, вирішивши пов'язане квадратне рівняння.	\(x^{2}-3 x+4=0\)
Напишіть квадратичну формулу.	\(x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
Потім підставляємо в значення\(a, b, c\).	\(x=\frac{-(-3) \pm \sqrt{(-3)^{2}-4 \cdot 1 \cdot(4)}}{2 \cdot 1}\)
Спростити.	\(x=\frac{3 \pm \sqrt{-7}}{2}\)
Спростити радиканд.	\(x=\frac{3 \pm \sqrt{7 i}}{2}\)
Складні рішення говорять нам, що парабола не перехоплює\(x\) -вісь. Також парабола відкривається вгору. Це говорить нам про те, що парабола повністю вище\(x\) -осі.	Комплексні рішення $.$ Малюнок 9.8.15

Визначення\(\PageIndex{1}\): Quadratic Inequality

Приклад\(\PageIndex{1}\): How to Solve a Quadratic Inequality Graphically

Вправа\(\PageIndex{1}\)

Вправа\(\PageIndex{2}\)

Приклад\(\PageIndex{2}\)

Вправа\(\PageIndex{3}\)

Вправа\(\PageIndex{4}\)

Приклад\(\PageIndex{3}\): How to Solve Quadratic Inequalities Algebraically

Вправа\(\PageIndex{5}\)

Вправа\(\PageIndex{6}\)

Приклад\(\PageIndex{4}\)

Вправа\(\PageIndex{7}\)

Вправа\(\PageIndex{8}\)

Приклад\(\PageIndex{5}\)

Вправа\(\PageIndex{9}\)

Вправа\(\PageIndex{10}\)

Крок 1: Запишіть квадратичну нерівність у стандартній формі.	Нерівність знаходиться в стандартній формі.	\(x^{2}-x-12 \geq 0\)
Крок 2: Визначте критичні точки - рішення відповідного квадратного рівняння.	Змініть знак нерівності на знак рівності, а потім вирішіть рівняння.	\(\begin{array}{c}{x^{2}-x-12=0} \\ {(x+3)(x-4)=0} \\ {x+3=0 \quad x-4=0} \\ {x=-3 \quad x=4}\end{array}\)
Крок 3: Використовуйте критичні точки, щоб розділити числову лінію на інтервали.	\(4\)Використовувати\(-3\) і розділити числову лінію на інтервали.	$Знімок екрана (4) .png$
Крок 4: Над числовим рядком покажіть знак кожного квадратичного виразу, використовуючи контрольні точки з кожного інтервалу, заміненого вихідною нерівністю.	Тест: \(x=-5\) \(x=0\) \(x=5\)	\(\begin{array}{ccc}{x^{2}-x-12} & {x^{2}-x-12} & {x^{2}-x-12} \\ {(-5)^{2}-(-5)-12} & {0^{2}-0-12} & {5^{2}-5-12} \\ {18} & {-12} & {8}\end{array}\) $Знімок екрана (5) .png$ Малюнок 9.8.11
Крок 5: Визначте інтервали, де нерівність правильна. Запишіть рішення в інтервальних позначеннях.	\(x^{2}-x-12 \geq 0\) Нерівність є позитивною в першому і останньому інтервалах і дорівнює\(0\) в точках\(-4,3\).	Рішення, в інтервальних позначеннях, є\((-\infty,-3] \cup[4, \infty)\).