8.7: Експоненціальне зростання і занепад

Моделі експоненціального зростання

Згадуючи дослідження в розділі 8.3, ми почали з розробки формули дискретного складного відсотка. Це призвело до іншої формули безперервного складного відсотка,

\(P(t) = P_{0}e^{rt}\), (1)

де\(P_{0}\) - початкова сума (основна сума) і r - річна процентна ставка в десятковій формі. Якщо гроші на банківському рахунку ростуть за річною ставкою r (за рахунок сплати відсотків), а якщо зростання постійно додається на рахунок (тобто відсотки постійно збільшуються), то залишок на рахунку в час t років дорівнює P (t), як це дається формулою (1).

Але ми можемо використовувати той самий аналіз для кількості, відмінної від грошей. Якщо P (t) являє собою кількість деякої кількості в час t років, а якщо P (t) зростає з річною швидкістю r при постійно додається зростанні, то ми можемо зробити висновок таким же чином, що P (t) повинен мати форму

\(P(t) = P_{0}e^{rt}\), (2)

де\(P_{0}\) - початкова сума в момент t = 0, а саме P (0).

Класичним прикладом є розкутий приріст населення. Якщо популяція P (t) певного виду поміщена в хороше середовище, з великою кількістю поживних речовин і простору для зростання, то вона буде рости за формулою (2). Наприклад, розмір бактеріальної культури в чашці Петрі буде дуже уважно слідувати цій формулі, якщо їй забезпечені оптимальні умови життя. Багато інших видів тварин і рослин також виявлять таку поведінку, якщо їх розміщувати в середовищі, в якому у них немає хижаків. Наприклад, коли британці завезли кроликів до Австралії в кінці 18 століття для полювання, популяція кроликів вибухнула, оскільки умови були хорошими для життя і розмноження, а природних хижаків кроликів не було.

ЕКСПОНЕНЦІАЛЬНЕ ЗРОСТАННЯ

Якщо функція P (t) постійно зростає зі швидкістю r > 0, то P (t) має вигляд

\(P(t) = P_{0}e^{rt}\), (3)

де\(P_{0}\) - початкова величина Р (0). У цьому випадку кількість P (t), як кажуть, демонструє експоненціальне зростання, а r - швидкість зростання.

Зауваження 4.

1. Якщо фізична величина (наприклад, популяція) зростає за формулою (3), ми говоримо, що кількість моделюється експоненціальною функцією зростання P (t).
2. Деякі можуть стверджувати, що зростання популяції кроликів, або навіть бактерій, насправді не є безперервним. Адже кролики народжуються по одному, тому популяція фактично росте дискретними шматками. Це, безумовно, вірно, але якщо населення велике, то зростання буде здаватися безперервним. Наприклад, розглянемо світову популяцію людей. У світі так багато людей, що щосекунди відбувається багато нових народжень і смертей. Таким чином, різниця в часі між кожною зміною 1 одиниці населення становить лише крихітну частку секунди, а отже дискретне зростання буде діяти практично так само, як і безперервне зростання. (Це аналогічно майже ідентичним результатам для безперервного складання та дискретного щоденного складання, які ми знайшли в розділі 8.3; складання кожної секунди або мілісекунди було б ще ближче.)
3. Так само використання формули безперервного експоненціального зростання (3) для моделювання дискретних величин іноді призводить до дробових відповідей. В цьому випадку результати потрібно буде округлити, щоб мати сенс. Наприклад, відповідь 224,57 кроликів насправді неможлива, тому відповідь слід округлити до 225.
4. У формулі (3), якщо час вимірюється роками (як ми це робили досі в цьому розділі), то r - річний темп приросту. Однак час можна виміряти в будь-яких зручних одиницях. Застосовується та ж формула, за винятком того, що швидкість зростання r задається в терміні конкретних одиниць часу, що використовуються. Наприклад, якщо час t вимірюється годинами, то r - погодинна швидкість зростання.

   У розділі 8.2 ми показали, що функція виду bt з b > 1 є експоненціальною

функція росту. Так само, якщо A > 0, то більш загальна експоненціальна функція\(Ab^t\) також демонструє експоненціальне зростання, оскільки графік\(Ab^t\) є лише вертикальним масштабуванням графіка\(b^t\). Однак функція експоненціального зростання у формулі (3), здається, відрізняється. Нижче ми покажемо, що функція насправді\(P_{0}e^{rt}\) може бути записана у вигляді\(Ab^t\) з b > 1.

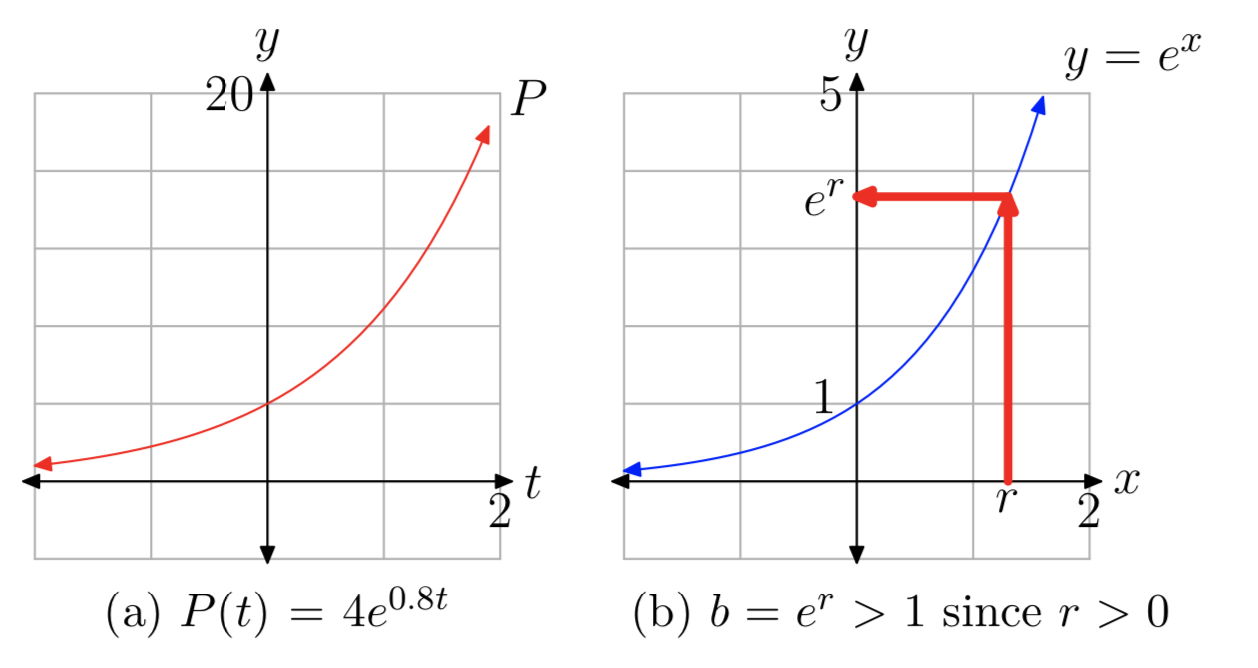
Давайте спочатку розглянемо конкретний приклад. Припустимо\(P(t) = 4e^{0.8t}\). Використовуючи Закони Експонентів, ми можемо переписати P (t) як

\(P(t) = 4e^{0.8t} = 4(e^{0.8})^t\). (5)

Так як\(e^{0.8} \approx 2.22554\), випливає, що

\(P(t) ≈ 4(2.22554)^t\).

Оскільки база\(\approx 2.22554\) більша за 1, це показує, що P (t) є експоненціальною функцією зростання, як показано на малюнку 1 (a)).

Тепер припустимо, що P (t) - це будь-яка функція форми\(P_{0}e^{rt}\) з r > 0. Як і в (5) вище, ми можемо використовувати Закони експонентів для перезапису P (t) як

\(P(t) = P_{0}e^{rt} = P_{0}(e^{r})^t = P_{0}b^t\)с\(b = e^r\).

Щоб довести, що b > 1, розглянемо графік,\(y = e^x\) показаний на малюнку 1 (б). Нагадаємо\(e \approx 2.718\), що, так e > 1, а значить\(y = e^x\) сама по собі експоненціальна крива зростання. Крім того, y-перехоплення є (0,1) з\(e^0 = 1\). Звідси випливає, що\(b = e^r > 1\) починаючи з r > 0 (див. Рис. 1 (б)).

Тому функції виду\(P(t) = P_{0}e^{rt}\) з r > 0 є експоненціальними функціями зростання.

Малюнок 1

Застосування експоненціального зростання

Зараз ми розглянемо роль функцій експоненціального зростання в деяких реальних програмах. У наступних прикладах припустимо, що популяція моделюється експоненціальною функцією зростання, як у формулі (3).

Приклад\(\PageIndex{6}\)

Припустимо, що населення певної країни зростає річними темпами на 2%. Якщо нинішнє населення становить 3 мільйони, яким буде населення через 10 років?

Це майбутня проблема вартості. Якщо вимірювати чисельність населення в мільйоні і раз в роках, то\(P(t) = P_{0}e^{rt}\) з\(P_{0} = 3\) і r = 0,02. Вставивши ці конкретні значення в формулу (3), отримаємо

\(P(t) = 3e^{0.02t}\).

Населення в 10 років становить\(P(10) = 3e^{(0.02)(10)} \approx 3.664208\) мільйон.

Приклад\(\PageIndex{7}\)

У тій же країні, що і в прикладі 6, скільки часу знадобиться населенню, щоб досягти 5 мільйонів?

Як і раніше,

\(P(t) = 3e^{0.02t}\).

Тепер ми хочемо дізнатися, коли майбутнє значення P (t) населення в якийсь час t дорівнюватиме 5 мільйонам. Тому нам потрібно вирішити рівняння P (t) = 5 за час t, що призводить до експоненціального рівняння

\(5 = 3e^{0.02t}\).

Використовуючи процедуру розв'язання експоненціальних рівнянь, представленої в розділі 8.6,

\(5 = 3e^{0.02t}\).

\(\rightarrow \frac{5}{3} = e^{0.02t}\)ізолювати експоненціальну

\(\rightarrow ln(\frac{5}{3}) = ln(e^{0.02t})\)застосувати функцію природного журналу

\(\rightarrow ln(\frac{5}{3}) = 0.02t\)так як\(ln(e^x) = x\)

\(\rightarrow \frac{ln(\frac{5}{3})}{0.02} = t\)ділити

\(\rightarrow t \approx 25.54128\)

Таким чином, знадобиться близько 25,54 років, щоб населення досягло 5 мільйонів.

Популяція бактерій зазвичай вимірюється вагою, як у наступних двох прикладах.

Приклад\(\PageIndex{8}\)

Припустимо, що розмір бактеріальної культури задається функцією

\(P(t) = 100e^{0.15t}\),

де розмір Р (t) вимірюється в грамах і час t вимірюється в годинами. Скільки часу знадобиться, щоб культура подвоїлася в розмірах?

Початковий розмір\(P_{0} = 100\) grams, so we want to know when the future value P (t), в якийсь час t буде дорівнює 200. Тому нам потрібно вирішити рівняння P (t) = 200 за час t, що призводить до експоненціального рівняння

\(200 = 100e^{0.15t}\).

Використовуючи ту ж процедуру, що і в останньому прикладі,

\(200 = 100e^{0.15t}\)

\(\rightarrow 2 = e^{0.15t}\)ізолювати експоненціальну

\(\rightarrow ln(2) = ln(e^{0.15t})\)застосувати функцію природного журналу

\(\rightarrow ln(2) = 0.15t\)так як\(ln(e^x) = x\)

\(\rightarrow \frac{ln(2)}{0.15} = t\)поділ

\(\rightarrow t \approx 4.620981\).

Таким чином, потрібно близько 4,62 години, щоб розмір збільшився вдвічі.

Останній приклад заслуговує додаткового коментаря. Припустимо, що ми почали з 1000 грам замість 100. Тоді для подвоєння в розмірі буде потрібно майбутнє значення в 2000 грам. Тому в цьому випадку нам доведеться вирішити рівняння

\(2000 = 1000e^{0.15t}\).

Але першим кроком є ізоляція експоненціальної, розділивши обидві сторони на 1000, щоб отримати

\(2 = e^{0.15t}\),

і це те ж саме, що і другий рядок рішення в останньому прикладі, тому відповідь буде такою ж. Так само повторення цього аргументу для будь-якої початкової суми призведе до того ж другого рядка, а отже, і тієї ж відповіді. Таким чином, час подвоєння залежить тільки від r, а не від початкової суми\(P_{0}\).

Моделі експоненціального розпаду

Ми спостерігали, що якщо кількість збільшується постійно зі швидкістю r, то вона моделюється за допомогою функції форми\(P(t) = P_{0}e^{rt}\). Але що робити, якщо замість цього кількість зменшується? Хоча ми не будемо представляти деталі тут, аналіз може бути проведений так само, як виведення формули безперервного компаундування в розділі 8.3. Єдина відмінність полягає в тому, що швидкість росту r у формулах має бути замінена на −r, оскільки кількість зменшується. Висновок полягає в тому, що величина моделюється функцією форми\(P(t) = P_{0}e^{−rt}\) замість\(P_{0}e^{rt}\).

ЕКСПОНЕНЦІАЛЬНИЙ РОЗПАД

Якщо функція P (t) постійно зменшується зі швидкістю r > 0, то P (t) має вигляд

\(P(t) = P_{0}e^{−rt}\), (9)

де\(P_{0}\) - початкова величина Р (0). У цьому випадку кількість P (t), як кажуть, проявляє експоненціальний розпад, а r - швидкість розпаду.

У розділі 8.2 ми показали, що функція виду bt з b < 1 є експоненціальною функцією розпаду. Аналогічно, якщо A > 0, то більш загальна експоненціальна функція\(Ab^t\) також проявляє експоненціальний розпад, оскільки графік\(Ab^t\) є лише вертикальним масштабуванням графіка bt. Однак функція експоненціального розпаду у формулі (9) виявляється іншою. Нижче ми покажемо, що функція насправді\(P_{0}e^{−rt}\) може бути записана у вигляді\(Ab^t\) з b < 1.

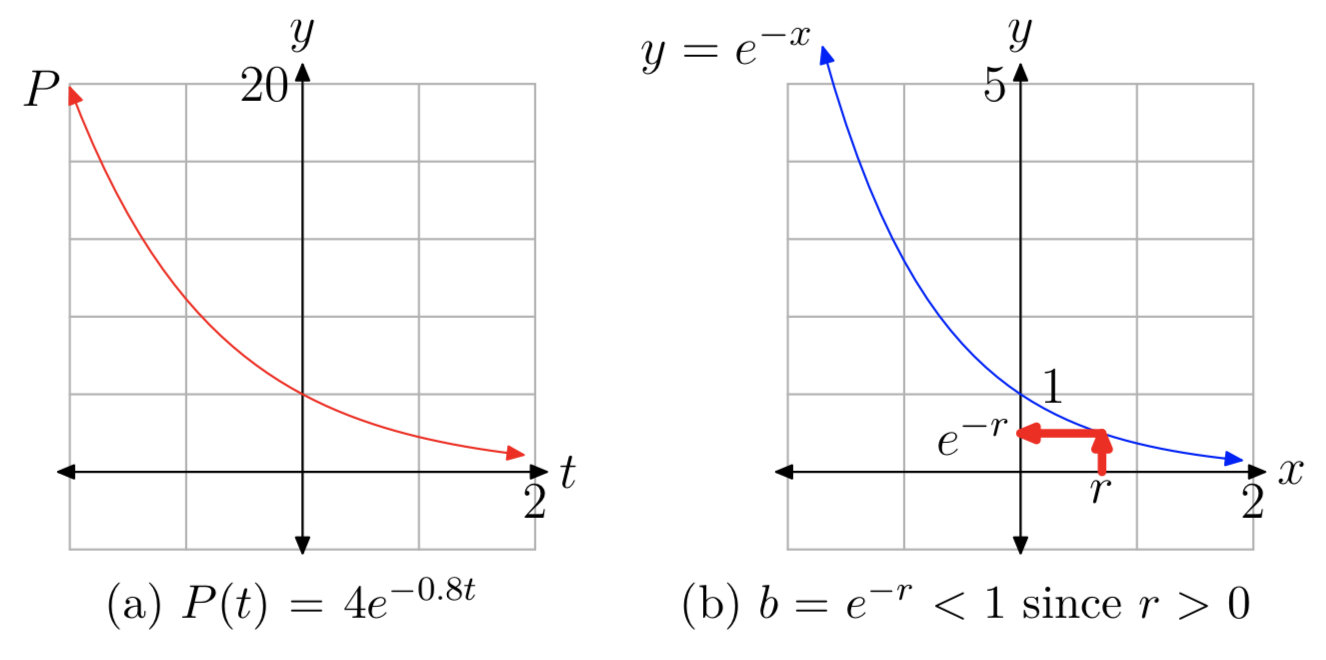
Давайте спочатку розглянемо конкретний приклад. Припустимо\(P(t) = 4e^{−0.8t}\). Використовуючи Закони Експонентів, ми можемо переписати P (t) як

\(P(t) = 4e^{−0.8t} = 4(e^{−0.8})^t\). (10)

Так як\(e^{−0.8} \approx 0.44933\), випливає, що

\(P(t) \approx 4(0.44933)^t\).

Оскільки основа менше 1,\(\approx 0.44933\) це показує, що P (t) є експоненціальною функцією розпаду, як показано на малюнку 2 (а)).

Тепер припустимо, що P (t) - це будь-яка функція форми\(P_{0}e^{−rt}\) з r > 0. Як і в (10) вище, ми можемо використовувати Закони експонентів, щоб переписати P (t) як

\(P(t) = P_{0}e^{−rt} = P_{0}(e^{−r})^t = P_{0}b^t\)с\(b = e^{−r}\).

Щоб довести, що b < 1, розглянемо графік,\(y = e^{−x}\) показаний на малюнку 2 (б). Зараз

\(e^{−x} = (e^{−1})^x =(\frac{1}{e})^x\)

і\(\frac{1}{e} \approx 0.36788 < 1\), так\(y = e^{−x}\) само по собі експоненціальна крива розпаду. (Крім того, ви можете спостерігати, що графік\(y = e^{−x}\) є відображенням графіка\(y = e^x\) поперек осі y.) Крім того, y-перехоплення є (0,1) з\(e^{−0} = 1\). Звідси випливає, що\(b = e^{−r} < 1\) починаючи з r > 0 (див. Рис.

Тому функції виду\(P(t) = P_{0}e^{−rt}\) з r > 0 є експоненціальними функціями розпаду.

Малюнок 2

Застосування експоненціального розпаду

Основним прикладом експоненціального розпаду є радіоактивний розпад. Радіоактивні елементи і ізотопи мимовільно виділяють субатомні частинки, і цей процес поступово змінює речовину в інший ізотоп. Наприклад, радіоактивний ізотоп Уран-238 з часом розпадається в стабільний ізотоп Свинець-206. Це випадковий процес для окремих атомів, але в цілому маса речовини зменшується за формулою експоненціального розпаду (9).

Приклад\(\PageIndex{11}\)

Припустимо, що певний радіоактивний елемент має річну швидкість розпаду 10%. Починаючи з 200 грамової проби елемента, скільки грам залишиться через 3 роки?

Це майбутня проблема вартості. Якщо вимірювати розмір в грамах і час в роках, то\(P(t) = P_{0}e^{−rt}\) з\(P_{0} = 200\) і r = 0,10. Вставивши ці конкретні значення в формулу (9), отримаємо

\(P(t) = 200e^{−0.10t}\).

Кількість в 3 роки -\(P(3) = 200e^{−(0.10)(3)} \approx 148.1636\) грами.

Приклад\(\PageIndex{12}\)

Використовуючи той самий елемент, що і в прикладі 11, якщо конкретний зразок елемента розпадається до 50 грам через 5 років, наскільки великим був вихідний зразок?

Це проблема теперішньої вартості, де невідомою є початкова сума\(P_{0}\). Як і раніше, r = 0. 10, так

\(P(t) = P_{0}e^{−0.10t}\).

Оскільки P (5) = 50, у нас є рівняння

\(50 = P(5) = P_{0}e^{−(0.10)(5)}\).

Це рівняння можна вирішити діленням:

\(\frac{50}{e^{−(0.10)(5)}} = P_{0}\)

Закінчіть, розрахувавши значення лівої сторони, щоб отримати\(P_{0} \approx 82.43606\) грами.

Приклад\(\PageIndex{13}\)

Припустимо, що певний радіоактивний ізотоп має річну швидкість розпаду 5%. Скільки років знадобиться, щоб 100-грамовий зразок розпався до 40 грам?

Використовувати\(P(t) = P_{0}e^{−​​​​​​​rt}\) з\(P_{0} = 100\) and r = 0. 05, так\(P(t) = 100e^{−0.05t}\).

Тепер ми хочемо дізнатися, коли майбутнє значення P (t) розміру вибірки в якийсь час t буде дорівнювати 40. Тому нам потрібно вирішити рівняння P (t) = 40 за час t, що призводить до експоненціального рівняння

\(40 = 100e^{−0.05t}\).

Використовуючи процедуру розв'язання експоненціальних рівнянь, представленої в розділі 8.6,

\(40 = 100e^{−0.05t}\)

\(\rightarrow 0.4 = e^{−0.05t}\)ізолювати експоненціальну

\(\rightarrow ln(0.4) = ln(e^{−0.05t})\)застосувати функцію природного журналу

\(\rightarrow ln(0.4) = −0.05t\)так як\(ln(e^x) = x\)

\(\rightarrow \frac{ln(0.4)}{−0.05} = t\)поділ

\(\rightarrow t \approx 18.32581\).

Таким чином, знадобиться приблизно 18, 33 роки, щоб зразок розпався до 40 грам.

Раніше ми бачили, що експоненціальні процеси зростання мають фіксований час подвоєння. Аналогічно, експоненціальні процеси розпаду мають фіксований період напіврозпаду, час, в якому одна половина початкової кількості розпадається.

Приклад\(\PageIndex{14}\)

Використовуючи той же елемент, що і в прикладі 13, що таке період напіврозпаду елемента?

Як і раніше, r = 0,05, так

\(P(t) = P_{0}e^{−0.05t}\).

Початковий розмір -\(P_{0}\) грами, тому ми хочемо знати, коли майбутнє значення P (t) в якийсь час t буде дорівнювати половині початкової кількості,\(\frac{P_{0}}{2}\). Тому нам потрібно вирішити рівняння\(P(t) = \frac{P_{0}}{2}\) за час t, що призводить до експоненціального рівняння

\(\frac{P_{0}}{2} = P_{0}e^{−0.05t}\).

Використовуючи ту ж процедуру, що і в останньому прикладі,

\(\frac{P_{0}}{2} = P_{0}e^{−0.05t}\)

\(\rightarrow \frac{1}{2} = e^{−0.05t}\)ізолювати експоненціальну

\(\rightarrow ln(\frac{1}{2}) = ln(e^{−0.05t})\)застосувати функцію природного журналу

\(\rightarrow ln(\frac{1}{2}) = −0.05t\)так як\(ln(e^x) = x\)

\(\rightarrow \frac{ln(\frac{1}{2})}{−0.05} = t\)поділ

\(\rightarrow t \approx 13.86294\)

Таким чином, період напіврозпаду становить приблизно 13.86 років.

Процес радіоактивного розпаду також становить основу методики датування вуглець-14. Атмосфера Землі містить крихітну кількість радіоактивного ізотопу вуглецю-14, а тому рослини і тварини також містять деяку кількість вуглецю-14 завдяки своїй взаємодії з атмосферою. Однак ця взаємодія закінчується, коли рослина або тварина гине, тому вуглець-14 починає розпадатися (швидкість розпаду становить 0,012%). Порівнюючи кількість вуглецю-14 в кістці, наприклад, з нормальною кількістю в живій тварині, вчені можуть обчислити вік кістки.

Приклад\(\PageIndex{15}\)

Припустимо, що в фрагменті кістки залишається лише 1,5% від нормальної кількості вуглецю-14. Скільки років кістки?

Використовувати\(P(t) = P_{0}e^{−rt}\) з r = 0.00012, так

\(P(t) = P_{0}e^{−0.00012t}\).

Початковий розмір -\(P_{0}\) грами, тому ми хочемо знати, коли майбутнє значення P (t) в якийсь час t буде дорівнювати 1,5% від початкової кількості,\(0.015P_{0}\). Тому нам потрібно вирішити рівняння\(P(t) = 0.015P_{0}\) за час t, що призводить до експоненціального рівняння

\(0.015P_{0} = P_{0}e^{−0.00012t}\).

Використовуючи ту саму процедуру, що і в прикладі 14,

\(0.015P_{0} = P_{0}e^{−0.00012t}\)

\(\rightarrow 0.015 = e^{−0.00012t}\)ізолювати експоненціальну

\(\rightarrow ln(0.015) = ln(e^{−0.00012t})\)застосувати функцію природного журналу

\(\rightarrow ln(0.015) = −0.00012t\)так як\(ln(e^x) = x\)

\(\rightarrow \frac{ln(0.015)}{−0.00012} = t\)поділ

\(\rightarrow t \approx 34998\)

Таким чином, кістки приблизно 34998 років.

Хоча техніка вуглецю-14 працює лише на рослині та тварині, існують інші подібні методи датування, використовуючи інші радіоактивні ізотопи, які використовуються на сьогоднішній день гірські породи та інші неорганічні речовини.

Вправа

Вправа\(\PageIndex{1}\)

Припустимо, що населення певного містечка зростає річними темпами на 6%. Якщо населення в даний час становить 5000, що це буде через 7 років? Округляйте відповідь до найближчого цілого числа.

Відповідь

7610 осіб

Вправа\(\PageIndex{2}\)

Припустимо, що населення певного містечка зростає річними темпами на 5%. Якщо населення в даний час становить 2000, скільки років знадобиться, щоб воно подвоїлося? Округлите свою відповідь до найближчої сотої.

Вправа\(\PageIndex{3}\)

Припустимо, що певний радіоактивний ізотоп має річну швидкість розпаду 7,2%. Скільки років знадобиться, щоб 227 грамова проба розпалася до 93 грам? Округлите свою відповідь до найближчої сотої.

Відповідь

12. 39 років

Вправа\(\PageIndex{4}\)

Припустимо, що певний радіоактивний ізотоп має річну швидкість розпаду 6,8%. Скільки років знадобиться, щоб 399 грамова проба розпалася до 157 грам? Округлите свою відповідь до найближчої сотої.

Вправа\(\PageIndex{5}\)

Припустимо, що населення певного містечка зростає річними темпами на 8%. Якщо населення в даний час становить 4000, скільки років знадобиться, щоб воно подвоїлося? Округлите свою відповідь до найближчої сотої.

Відповідь

8. 66 років

Вправа\(\PageIndex{6}\)

Припустимо, що певний радіоактивний ізотоп має річну швидкість розпаду 19,2%. Починаючи з зразка 443 грам, скільки грам залишиться через 9 років? Округлите свою відповідь до найближчої сотої.

Вправа\(\PageIndex{7}\)

Припустимо, що певний радіоактивний ізотоп має річну швидкість розпаду 17,4%. Що таке період напіврозпаду (в роках) ізотопу? Округлите свою відповідь до найближчої сотої.

Відповідь

3. 98 років

Вправа\(\PageIndex{8}\)

Припустимо, що населення певного містечка зростає річними темпами на 7%. Якщо населення в даний час становить 8000, скільки років знадобиться, щоб воно досягло 18 000? Округлите свою відповідь до найближчої сотої.

Вправа\(\PageIndex{9}\)

Припустимо, що певний радіоактивний ізотоп має річну швидкість розпаду 17,3%. Починаючи з 214 грамової проби, скільки грам залишиться через 5 років? Округлите свою відповідь до найближчої сотої.

Відповідь

90. 11г

Вправа\(\PageIndex{10}\)

Припустимо, що населення певного містечка зростає річними темпами на 7%. Якщо населення зросте до 2000 за 7 років, якою була вихідна популяція? Округляйте відповідь до найближчого цілого числа.

Вправа\(\PageIndex{11}\)

Припустимо, що населення певного містечка зростає річними темпами на 3%. Якщо населення в даний час становить 3000, скільки років знадобиться, щоб воно подвоїлося? Округлите свою відповідь до найближчої сотої.

Відповідь

23. 10 років

Вправа\(\PageIndex{12}\)

Припустимо, що певний радіоактивний ізотоп має річну швидкість розпаду 12,5%. Починаючи з 127 грамової проби, скільки грам залишиться через 6 років? Округлите свою відповідь до найближчої сотої.

Вправа\(\PageIndex{13}\)

Припустимо, що певний радіоактивний ізотоп має річну швидкість розпаду 13,1%. Припустимо, що певний радіоактивний ізотоп має річну швидкість розпаду 13,1%

Відповідь

141. 10 г

Вправа\(\PageIndex{14}\)

Припустимо, що населення певного містечка зростає річними темпами на 2%. Якщо населення зросте до 9 000 за 4 роки, якою була первісна популяція? Округляйте відповідь до найближчого цілого числа.

Вправа\(\PageIndex{15}\)

Припустимо, що населення певного містечка зростає річними темпами на 2%. Якщо населення в даний час становить 7000, скільки років знадобиться, щоб воно подвоїлося? Округлите свою відповідь до найближчої сотої.

Відповідь

34. 66 років

Вправа\(\PageIndex{16}\)

Припустимо, що певний радіоактивний ізотоп має річну швидкість розпаду 5,3%. Скільки років знадобиться, щоб 217 грамова проба розпалася до 84 грам? Округлите свою відповідь до найближчої сотої.

Вправа\(\PageIndex{17}\)

Припустимо, що певний радіоактивний ізотоп має річну швидкість розпаду 18,7%. Скільки років знадобиться, щоб 324 грамова проба розпалася до 163 грам? Округлите свою відповідь до найближчої сотої.

Відповідь

3. 67 років

Вправа\(\PageIndex{18}\)

Припустимо, що населення певного містечка зростає річними темпами на 8%. Якщо населення в даний час становить 8000, скільки років знадобиться, щоб воно досягло 18 000? Округлите свою відповідь до найближчої сотої.

Вправа\(\PageIndex{19}\)

Припустимо, що певний радіоактивний ізотоп має річну швидкість розпаду 2,3%. Якщо конкретний зразок розпадається до 25 грам через 8 років, наскільки великим (у грамах) був вихідний зразок? Округлите свою відповідь до найближчої сотої.

Відповідь

30. 0,5 г

Вправа\(\PageIndex{20}\)

Припустимо, що населення певного містечка зростає річними темпами на 4%. Якщо населення в даний час становить 7000, скільки років знадобиться, щоб воно досягло 17 000? Округлите свою відповідь до найближчої сотої.

Вправа\(\PageIndex{21}\)

Припустимо, що певний радіоактивний ізотоп має річну швидкість розпаду 9,8%. Якщо конкретний зразок розпадається до 11 грам через 6 років, наскільки великим (у грамах) був вихідний зразок? Округлите свою відповідь до найближчої сотої.

Відповідь

19. 80 г

Вправа\(\PageIndex{22}\)

Припустимо, що населення певного містечка зростає річними темпами на 5%. Якщо населення зросте до 6000 за 3 роки, якою була первісна популяція? Округляйте відповідь до найближчого цілого числа.

Вправа\(\PageIndex{23}\)

Припустимо, що населення певного містечка зростає річними темпами на 8%. Якщо населення в даний час становить 6000, що це буде через 5 років? Округляйте відповідь до найближчого цілого числа.

Відповідь

8 951 осіб

Вправа\(\PageIndex{24}\)

Припустимо, що певний радіоактивний ізотоп має річну швидкість розпаду 15,8%. Що таке період напіврозпаду (в роках) ізотопу? Округлите свою відповідь до найближчої сотої.

Вправа\(\PageIndex{25}\)

Припустимо, що населення певного містечка зростає річними темпами на 9%. Якщо населення зросте до 7000 за 5 років, якою була первісна популяція? Округляйте відповідь до найближчого цілого числа.

Відповідь

8 951 осіб

Вправа\(\PageIndex{26}\)

Припустимо, що певний радіоактивний ізотоп має річну швидкість розпаду 18,6%. Якщо конкретний зразок розпадається до 41 грама через 3 роки, наскільки великим (у грамах) був вихідний зразок? Округлите свою відповідь до найближчої сотої.

Вправа\(\PageIndex{27}\)

Припустимо, що певний радіоактивний ізотоп має річну швидкість розпаду 5,2%. Що таке період напіврозпаду (в роках) ізотопу? Округлите свою відповідь до найближчої сотої.

Відповідь

13. 33 років

Вправа\(\PageIndex{28}\)

Припустимо, що певний радіоактивний ізотоп має річну швидкість розпаду 6,5%. Що таке період напіврозпаду (в роках) ізотопу? Округлите свою відповідь до найближчої сотої.

Вправа\(\PageIndex{29}\)

Припустимо, що населення певного містечка зростає річними темпами на 8%. Якщо населення в даний час становить 2000, скільки років знадобиться, щоб воно досягло 7000? Округлите свою відповідь до найближчої сотої.

Відповідь

15. 66 років

Вправа\(\PageIndex{30}\)

Припустимо, що певний радіоактивний ізотоп має річну швидкість розпаду 3,7%. Якщо конкретний зразок розпадається до 47 грам через 8 років, наскільки великим (у грамах) був вихідний зразок? Округлите свою відповідь до найближчої сотої.

Вправа\(\PageIndex{31}\)

Припустимо, що населення певного містечка зростає річними темпами на 6%. Якщо населення в даний час становить 7 000, що це буде через 7 років? Округляйте відповідь до найближчого цілого числа.

Відповідь

10 654 осіб

Вправа\(\PageIndex{32}\)

Припустимо, що населення певного містечка зростає річними темпами на 4%. Якщо населення в даний час становить 1000, що це буде через 3 роки? Округляйте відповідь до найближчого цілого числа.

У вправах 33 - 40 використовують той факт, що швидкість розпаду вуглецю-14 становить 0,012%. Округліть відповідь до найближчого року.

Вправа\(\PageIndex{33}\)

Припустимо, що в фрагменті кістки залишається всього 8,6% від нормальної кількості вуглецю-14. Скільки років кістки?

Відповідь

20 45 років

Вправа\(\PageIndex{34}\)

Припустимо, що в фрагменті кістки залишається всього 5,2% від нормальної кількості вуглецю-14. Скільки років кістки?

Вправа\(\PageIndex{35}\)

Припустимо, що 90,1% від нормальної кількості вуглецю-14 залишається в шматку дерева. Скільки років деревині?

Відповідь

869 років

Вправа\(\PageIndex{36}\)

Припустимо, що 83,6% від нормальної кількості вуглецю-14 залишається в шматку тканини. Скільки років тканині?

Вправа\(\PageIndex{37}\)

Припустимо, що в фрагменті кістки залишається лише 6,2% від нормальної кількості вуглецю-14. Скільки років кістки?

Відповідь

23 172 років

Вправа\(\PageIndex{38}\)

Припустимо, що в фрагменті кістки залишається лише 1,3% від нормальної кількості вуглецю-14. Скільки років кістки?

Вправа\(\PageIndex{39}\)

Припустимо, що 96,7% від нормальної кількості вуглецю-14 залишається в шматку тканини. Скільки років тканині?

Відповідь

280 років

Вправа\(\PageIndex{40}\)

Припустимо, що 84,9% від нормальної кількості вуглецю-14 залишається в шматку дерева. Скільки років деревині?

​​​​​​​