4.4: Застосування лінійних систем

Last updated
Save as PDF

Page ID: 58254

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Налаштуйте та вирішуйте програми, що включають відносини між числами.
Налаштовуйте та вирішуйте додатки, що включають відсотки та гроші.
Налаштуйте та вирішуйте проблеми суміші.
Налаштуйте та вирішуйте проблеми рівномірного руху (задачі відстані).

Проблеми, пов'язані з відносинами між реальними числами

Тепер у нас є методи, необхідні для вирішення лінійних систем. З цієї причини ми більше не обмежуємося використанням однієї змінної при налаштуванні рівнянь, які моделюють додатки. Якщо перевести додаток в математичну установку за допомогою двох змінних, то нам потрібно сформувати лінійну систему з двома рівняннями.

Приклад$\PageIndex{1}$

Сума двох чисел є$40$ і їх різниця дорівнює$8$. Знайдіть цифри.

Рішення:

Визначте змінні:

$x$Дозволяти представляти одне з невідомих чисел.

$y$Дозволяти представляти інше невідоме число.

Налаштуйте рівняння:

При використанні двох змінних нам потрібно встановити два рівняння. Перша ключова фраза «сума двох чисел є$40$» перекладається наступним чином:

$x+y=40$

А друга ключова фраза, «різниця є»$8$, веде нас до другого рівняння:

$x-y=8$

Тому наша алгебраїчна установка складається з наступної системи:

$\left\{\begin{aligned} x+y&=40 \\ x-y&=8 \end{aligned}\right.$

Вирішити :

Вирішити отриману систему ми можемо будь-яким методом на наш вибір. Тут ми вибираємо вирішити шляхом усунення. Додавання рівнянь разом усуває змінну$y$.

$\begin{aligned} x\color{red}{+y}&=40 \\ \underline{+\quad x\color{red}{-y}}&\underline{=8} \\ 2x&=48 \\ x&=24 \end{aligned}$

Після того, як ми маємо$x$, назад замінюємо, щоб знайти$y$.

$\begin{aligned} x+y&=40 \\ \color{OliveGreen}{24}\color{black}{+y}&=40 \\ 24+y\color{Cerulean}{-24}&=40\color{Cerulean}{-24} \\ y&=16 \end{aligned}$

Перевірка:

Сума двох чисел повинна бути$42$ і їх різниця$8$.

$\begin{aligned} 24+16&=40 \\ 24-16&=8 \end{aligned}$

Відповідь:

Два числа -$24$ і$16$.

Приклад$\PageIndex{2}$

Сума$9$ разів більша кількість і в два рази менша$6$. Різниця$3$ разів більша і менша$7$. Знайдіть цифри.

Рішення:

Почніть з присвоєння змінних більшому і меншому числу.

$x$Дозволяти представляти більшу кількість.

$y$Дозволяти представляти меншу кількість.

Перше речення описує суму, а друге речення описує різницю.

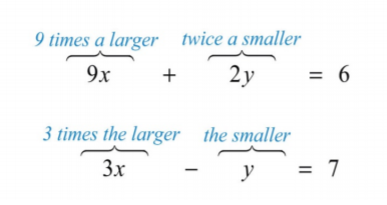Знімок екрана (416) .png — Малюнок$\PageIndex{1}$

Це призводить до наступної системи:

$\left\{\begin{aligned} 9x+2y&=6\\3x-y&=7 \end{aligned}\right.$

Вирішити за допомогою методу усунення. Друге рівняння множимо на$2$ і складаємо.

$\left\{\begin{aligned} 9x+2y&=6 \\ 3x-y&=7 \end{aligned}\right. \stackrel{\times 2}{\Rightarrow} \left\{\begin{aligned} 9x+2y&=6\\ 6x-2y&=14 \end{aligned}\right.$

$\begin{aligned} 9x\color{red}{+2y}&=6\\ \underline{+\quad 6x\color{red}{-2y}}&\underline{=14} \\ 15x&=20 \\ x&=\frac{20}{15} \\ x&=\frac{4}{3} \end{aligned}$

Назад замінник знайти$y$.

Відповідь:

Чим більше число$\frac{4}{3}$ і тим менше число$−3$.

Вправа$\PageIndex{1}$

Сума двох чисел дорівнює$3$. Коли вдвічі менше число віднімається з$6$ разів, тим більший результат$22$. Знайдіть цифри.

Відповідь: Два числа -$−\frac{1}{2}$ і$\frac{7}{2}$.

Проблеми з відсотками та грошима

У цьому розділі проблеми з відсотками та грошима повинні здатися знайомими. Різниця полягає в тому, що ми будемо використовувати дві змінні при налаштуванні алгебраїчних рівнянь.

Приклад$\PageIndex{3}$

Рулон$32$ купюр містить лише $$5$ купюри та $$10$ купюри. Якщо значення рулону дорівнює $$220$, то скільки кожної купюри в рулоні?

Рішення:

Почніть з ідентифікації змінних.

$x$Дозволяти представляти кількість $$5$ купюр.

$y$Дозволяти представляти кількість $$10$ купюр.

При використанні двох змінних нам потрібно встановити два рівняння. Перше рівняння створюється з того, що є$32$ купюри.

$x+y=32$

Друге рівняння підсумовує значення кожної купюри: загальна величина дорівнює $$220$.

$$5\cdot x+$ $$10\cdot y=$ $$220$

Представте обидва рівняння як систему; це наша алгебраїчна установка.

$\left\{\begin{aligned} x+y&=32 \\ 5x+10y&=220 \end{aligned}\right.$

Тут ми вирішили вирішити шляхом ліквідації, хоча заміна працювала б так само добре. Усунути$x$ шляхом множення першого рівняння на$−5$.

Тепер складіть рівняння разом:

Після того$y$, як ми маємо, кількість $$10$ купюр, назад замінити, щоб знайти$x$.

$\begin{aligned} x+y&=32 \\ x+\color{OliveGreen}{12}&=32 \\ x+12\color{Cerulean}{-12}&=32\color{Cerulean}{-12} \\ x&=20 \end{aligned}$

Відповідь:

Є двадцять $$5$ купюр і дванадцять $$10$ купюр. Чек залишається на зчитувач.

Приклад$\PageIndex{4}$

Всього в два рахунки$6,300$ було вкладено $. Частина була інвестована в компакт-диск під$4\frac{1}{2}$% річної процентної ставки, а частина була вкладена в фонд грошового ринку під$3\frac{3}{4}$% річної процентної ставки. Якщо загальний простий відсоток за один рік склав $$267.75$, то скільки було вкладено в кожен рахунок?

Рішення:

Дозвольте$x$ представляти суму вкладеного в$4\frac{1}{2}$%$=4.5$%$=0.045$

Дозвольте$y$ представляти суму вкладеного в$3\frac{3}{4}$%$=3.75$%$=0.0375$

Загальна сума на обох рахунках може бути виражена у вигляді

$x+y=6,300$

Щоб встановити друге рівняння, використовуйте той факт, що сумарний відсоток склав $$267.75$. Нагадаємо, що відсотки за один рік - це процентна ставка в рази більше основної суми$(I=prt=pr⋅1=pr)$. Використовуйте це, щоб додати відсотки в обох облікових записах. Обов'язково використовуйте десяткові еквіваленти для процентних ставок, заданих у відсотках.

$\begin{array}{ccccc}{\color{Cerulean}{interest\:from\:the\:CD}}&{\color{Cerulean}{+}}&{\color{Cerulean}{interest\:from\:the\:fund}}&{\color{Cerulean}{=}}&{\color{Cerulean}{total\:interest}}\\{0.045x}&{+}&{0.375y}&{=}&{267.75} \end{array}$

Ці два рівняння разом утворюють наступну лінійну систему:

$\left\{\begin{aligned} x+y&=6,300 \\ 0.045x+0.0375y&=267.75 \end{aligned}\right.$

Усунути$y$ шляхом множення першого рівняння на$−0.0375$.

$\left\{\begin{aligned} x+y&=6,300 \\ 0.045x+0.0375y&=267.75 \end{aligned}\right. \stackrel{\times (-0.0375)}{\Rightarrow} \left\{\begin{aligned} -0.0375x-0.0375y&=-236.25 \\ 0.045x+0.0375y&=267.75 \end{aligned}\right.$

Далі складіть рівняння разом, щоб усунути змінну$y$.

$\begin{aligned} -0.0375x\color{red}{-0.0375y}&=-236.25 \\ \underline{+\quad 0.045x\color{red}{+0.0375y}}&\underline{=267.75} \\ 0.0075x&=31.5 \\ \frac{0.0075x}{\color{Cerulean}{0.0075}}&=\frac{31.5}{\color{Cerulean}{0.0075}} \\ x&=4,200 \end{aligned}$

Замінник назад.

$\begin{aligned} x+y&=6,300 \\ \color{OliveGreen}{4,200}\color{black}{+y}&=6,300 \\ 4,200+y\color{Cerulean}{-4,200}&=6,300\color{Cerulean}{-4,200} \\ y&=2,100 \end{aligned}$

Відповідь:

$$4,200$ було інвестовано під$4\frac{1}{2}$%, а $$2,100$ було інвестовано під$3\frac{3}{4}$%

На даний момент ми повинні мати можливість вирішувати ці типи проблем двома способами: з однією змінною, а тепер з двома змінними. Налаштування проблем зі словами з двома змінними часто спрощує весь процес, особливо коли відносини між змінними не настільки зрозумілі.

Вправа$\PageIndex{2}$

У перший день дводенної зустрічі були придбані$10$ кави та$10$ пончики на загальну суму $$20.00$. Оскільки ніхто не пив каву і всі пончики були з'їдені, наступного дня були придбані лише$2$ кави та$14$ пончики на загальну суму $$13.00$. Скільки коштувала кожна кава і кожен пончик?

Відповідь: Кава: $$1.25$; пончик: $$0.75$

Проблеми сумішей

Проблеми з сумішшю часто включають відсоток і деяку загальну суму. Важливо розмежувати ці два типи величин. Наприклад, якщо проблема говорить про те, що ємність$20$ -унція заповнена$2$% сольовим (сольовим) розчином, то це означає, що ємність заповнюється сумішшю солі і води наступним чином:

Таблиця$\PageIndex{1}$
	Відсоток	Сума
Сіль	$2$%$=0.02$	$0.02(20$унцій)$=0.4$ унцій
Вода	$98$%$=0.98$	$0.98(20$унцій)$=19.6$ унцій

Іншими словами, множимо відсоток на загальну суму, щоб отримати кількість кожної частини суміші.

Приклад$\PageIndex{5}$

$2$% сольовий розчин повинен бути об'єднаний і змішаний$5$ з% сольовим розчином для отримання$72$ унцій сольового розчину$2.5$%. Скільки потрібно кожного?

Рішення:

$x$Дозволяти представляти кількість необхідного сольового розчину$2$%.

$y$Дозволяти представляти кількість необхідного сольового розчину$5$%.

Загальна кількість сольового розчину, необхідного -$72$ унції. Це призводить до одного рівняння,

$x+y=72$

Друге рівняння додає кількість солі в правильних відсотках. Кількість солі отримують шляхом множення в процентному співвідношенні на кількість, де змінні$x$ і$y$ представляють кількості розчинів.

$\begin{array}{ccccc}{\color{Cerulean}{salt\:in2\%\:solution}}&{\color{Cerulean}{+}}&{\color{Cerulean}{salt\:in\:5\%\:solution}}&{\color{Cerulean}{=}}&{\color{Cerulean}{salt\:in\:the\:end\:solution}}\\{0.02x}&{+}&{0.05y}&{=}&{0.025(72)}\end{array}$

Вирішити.

$\left\{\begin{aligned} x+y&=72 \\ 0.02x+0.05y&=0.025(72) \end{aligned}\right. \stackrel{\times (-0.02)}{\Rightarrow} \left\{\begin{aligned} -0.02x-0.02y&=-1.44 \\ 0.02x+0.05y&=1.8 \end{aligned}\right.$

$\begin{aligned} \color{red}{-0.02x}\color{black}{-0.02y}&=-1.44 \\ \underline{+\quad\color{red}{0.02x}\color{black}{+0.05y}}&\underline{=1.8} \\ 0.03y&=0.36 \\ \frac{0.03y}{\color{Cerulean}{0.03}}&=\frac{0.36}{\color{Cerulean}{0.03}} \\ y&=12 \end{aligned}$

Замінник назад.

$\begin{aligned} x+y&=72 \\ x+\color{OliveGreen}{12}&=72 \\ x+12\color{Cerulean}{-12}&=72\color{Cerulean}{-12} \\ x&=60 \end{aligned}$

Відповідь:

Нам потрібні$60$ унції$2$% сольового розчину і$12$ унції$5$% сольового розчину.

Приклад$\PageIndex{6}$

$50$% спиртовий розчин змішують з$10$% спиртовим розчином для створення$8$ -унційної суміші з$32$% спиртового розчину. Скільки потрібно кожного?

Рішення:

$x$Дозволяти представляти кількість необхідного$50$% спиртового розчину.

$y$Дозволяти представляти кількість необхідного$10$% спиртового розчину.

Загальна кількість суміші повинна складати$8$ унції.

$x+y=8$

Друге рівняння додає кількість спирту з кожного розчину в правильних відсотках. Кількість алкоголю в кінцевому результаті$32$ становить%$8$ унцій, або$0.032(8)$.

$\begin{array}{ccccc}{\color{Cerulean}{alcohol\:in\:50\%\:solution}}&{\color{Cerulean}{+}}&{\color{Cerulean}{alcohol\:in\:10\%\:solution}}&{\color{Cerulean}{=}}&{\color{Cerulean}{alcohol\:in\:the\:end\:solution}}\\{0.50x}&{+}&{0.10y}&{=}&{0.32(8)}\end{array}$

Тепер ми можемо сформувати систему з двох лінійних рівнянь і двох змінних наступним чином:

$\left\{\begin{aligned} x+y&=8 \\ 0.50x+0.10y&=0.32(8) \end{aligned}\right.$

У цьому прикладі помножте друге рівняння на,$100$ щоб усунути десяткові числа. Крім того, помножте перше рівняння на,$−10$ щоб вирівняти змінну$y$ для усунення.

$\begin{array}{c|c} {Equation\:1:}&{Equation\:2:}\\{\color{Cerulean}{-10}\color{black}{(x+y)=}\color{Cerulean}{-10}\color{black}{(8)}}&{\color{Cerulean}{100}\:\color{black}{0.50x+0.10y=}\color{Cerulean}{100}\color{black}{(0.32)(8)}}\\{-10x-10y=-80}&{50x+10y=256} \end{array}$

Отримуємо наступну еквівалентну систему:

Додайте рівняння, а потім вирішіть для$x$:

Замінник назад.

$\begin{aligned} x+y&=8 \\ \color{OliveGreen}{4.4}\color{black}{+y}&=8 \\ 4.4+y\color{Cerulean}{-4.4}&=8\color{Cerulean}{-4.4} \\ x&=3.6 \end{aligned}$

Відповідь:

Для отримання$8$ унцій спиртової суміші$32$% нам потрібно змішати$4.4$ унції$50$% спиртового розчину і$3.6$ унції$10$% розчину.

Вправа$\PageIndex{3}$

Концентрат антифризу$70$% змішують з водою для отримання$5$ галонної суміші, що містить$28$% антифризу. Скільки потрібно води і концентрату антифризу?

Відповідь: Нам потрібно змішати$3$ галони води з$2$ галонами концентрату антифризу.

Проблеми рівномірного руху (задачі відстані)

Нагадаємо, що пройдена відстань дорівнює середньому показнику часу, що пройшов з цією швидкістю,$D=r⋅t$.

Ці проблеми рівномірного руху зазвичай мають багато даних, тому це допомагає спочатку організувати ці дані в діаграмі, а потім налаштувати лінійну систему. У цьому розділі пропонується використовувати дві змінні.

Приклад$\PageIndex{7}$

Виконавчий проїхав загалом$8$ години і$1,930$ милі на машині та літаку. Під'їжджаючи до аеропорту на машині, вона набирала в середньому$60$ кілометри на годину. У повітрі літак в середньому становив$350$ милі на годину. Скільки часу їй знадобилося, щоб доїхати до аеропорту?

Рішення:

Нас просять знайти час, який потрібен їй, щоб доїхати до аеропорту; це вказує на те, що час - невідома кількість.

Нехай$x$ уявляють час, який знадобився, щоб доїхати до аеропорту.

Нехай$y$ уявляють собою час, проведений в повітрі.

Знімок екрана (417) .png — Малюнок$\PageIndex{2}$

Використовуйте формулу$D=r⋅t$, щоб заповнити невідомі відстані.

$\color{Cerulean}{Distance\:traveled\:in\:the\:car:}\quad\color{black}{D=r\cdot t=60\cdot x}$

$\color{Cerulean}{Distance\:traveled\:in\:the\:air:}\quad\color{black}{D=r\cdot t=350\cdot y}$

Знімок екрана (418) .png — Малюнок$\PageIndex{3}$

Стовпець відстані та стовпчик часу діаграми допомагають нам налаштувати наступну лінійну систему.

Знімок екрана (419) .png — Малюнок$\PageIndex{4}$

$\left\{\begin{aligned} x+y&=8 &\color{Cerulean}{\leftarrow\:total\:time\:traveled} \\ 6-x+350y&=1,930 &\color{Cerulean}{\leftarrow\:total\:distance\:traveled} \end{aligned}\right.$

Вирішити.

Тепер назад замінюємо, щоб знайти час, який знадобився, щоб доїхати до аеропорту$x$:

$\begin{aligned} x+y&=8 \\ x+\color{OliveGreen}{5}&=8 \\ x&=3 \end{aligned}$

Відповідь:

Їй знадобилися$3$ години, щоб доїхати до аеропорту.

Не завжди так, що час - це невідома кількість. Уважно прочитайте проблему та визначте, що вас попросять знайти; це визначає ваші змінні.

Приклад$\PageIndex{8}$

Літаючи з вітром, літак проїжджав$1,365$ милі за$3$ годинами. Потім літак повернувся проти вітру і проїхав ще$870$ милі за$2$ години. Знайти швидкість літака і швидкість вітру.

Рішення:

Явної залежності між швидкістю літака і швидкістю вітру немає. З цієї причини використовуйте дві змінні наступним чином:

$x$Дозволяти представляти швидкість літака.

Нехай$w$ представляють швидкість вітру.

Використовуйте наступну діаграму, щоб упорядкувати дані:

Скріншот (420) .png — Малюнок$\PageIndex{5}$

З вітром загальна швидкість літака становить$x+w$. Літаючи проти вітру, загальна швидкість дорівнює$x−w$.

Знімок екрана (421) .png — Малюнок$\PageIndex{6}$

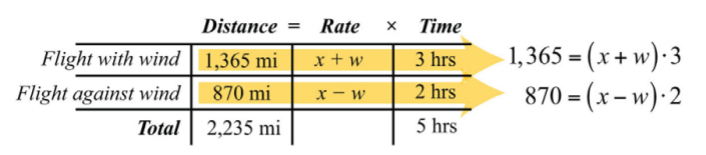
Використовуйте рядки діаграми разом з формулою$D=r⋅t$ для побудови лінійної системи, яка моделює цю задачу. Подбайте про те, щоб згрупувати величини, що представляють норму в дужках.

Знімок екрана (422) .png — Малюнок$\PageIndex{7}$

$\left\{\begin{aligned} 1,365&=(x+w)\cdot 3 &\color{Cerulean}{\leftarrow\:distance\:traveled\:with\:the\:wind} \\ 870&=(x-w)\cdot 2 &\color{Cerulean}{\leftarrow\:distance\:traveled\:against\:the\:wind} \end{aligned}\right.$

Якщо розділити обидві сторони першого рівняння на$3$ і обидві сторони другого рівняння на$2$, то отримаємо наступну еквівалентну систему:

$\left\{\begin{aligned} 1,365&=(x+w)\cdot 3 \\ 870&=(x-w)\cdot 2 \end{aligned}\right. \begin{aligned} &\stackrel{\div 3}{\Rightarrow} \\ &\stackrel{\div 2}{\Rightarrow} \end{aligned} \left\{\begin{aligned} 455&=x+w \\ 435&=x-w \end{aligned}\right.$

$\begin{aligned} x\color{red}{+w}&=455 \\ \underline{+\quad x\color{red}{-w}}&\underline{=435} \\ 2x&=890 \\ \frac{2x}{\color{Cerulean}{2}}&=\frac{890}{\color{Cerulean}{2}} \\ x&=455 \end{aligned}$

Замінник назад.

$\begin{aligned} x+w&=455 \\ \color{OliveGreen}{455}\color{black}{+w}&=455 \\ w&=10 \end{aligned}$

Відповідь:

Швидкість літака -$445$ милі на годину, а швидкість вітру -$10$ милі на годину.

Вправа$\PageIndex{4}$

Човен проїхав$24$ милі вниз за течією за$2$ годинами. Зворотна поїздка, яка була проти течії, зайняла в два рази більше часу. Які швидкості човна і течії?

Відповідь: Швидкість човна -$9$ милі на годину, а швидкість течії -$3$ милі на годину.

Ключові виноси

Використовуйте дві змінні як засіб для спрощення алгебраїчної установки додатків, де зв'язок між невідомими незрозумілий.
Уважно прочитайте проблему кілька разів. Якщо використовуються дві змінні, то пам'ятайте, що для вирішення задачі потрібно встановити два лінійних рівняння.
Обов'язково відповісти на питання у формі пропозиції і включити правильні одиниці для відповіді.

Вправа$\PageIndex{5}$ Applications Involving Numbers

Налаштуйте лінійну систему і вирішуйте.

Сума двох цілих чисел дорівнює$54$ і їх різниця дорівнює$10$. Знайти цілі числа.
Сума двох цілих чисел дорівнює$50$ і їх різниця дорівнює$24$. Знайти цілі числа.
Сума двох натуральних чисел дорівнює$32$. Коли менше ціле число віднімається з подвоєного більшого, результат буде$40$. Знайдіть два цілих числа.
Сума двох натуральних чисел дорівнює$48$. Коли двічі менше ціле число віднімається від більшого, результат є$12$. Знайдіть два цілих числа.
Сума двох цілих чисел дорівнює$74$. Чим$26$ більше, ніж в два рази, тим менше. Знайдіть два цілих числа.
Сума двох цілих чисел дорівнює$45$. Чим більше$3$ менше, ніж в три рази, тим менше. Знайдіть два цілих числа.
Сума двох чисел дорівнює нулю. Коли$4$ раз менше число додається в$8$ рази більше, результат є$1$. Знайдіть два числа.
Сума більшого числа і$4$ разів меншого числа дорівнює$5$. Коли$8$ раз менше віднімається з удвічі більше, результат є$−2$. Знайдіть цифри.
Сума$12$ разів більша кількість і$11$ разів менше$−36$. Різниця$12$ разів більша і$7$ рази менша$36$. Знайдіть цифри.
Сума$4$ разів більша кількість і$3$ разів менше$7$. Різниця$8$ разів більша і$6$ рази менша$10$. Знайдіть цифри.

Відповідь

1. Цілими числами є$22$ і$32$.

3. Цілими числами є$8$ і$24$.

5. Цілими числами є$16$ і$58$.

7. Два числа -$−\frac{1}{4}$ і$\frac{1}{4}$.

9. Чим менше число$−4$ і тим більше$\frac{2}{3}$.

Вправа$\PageIndex{6}$ Interest and Money Problems

Налаштуйте лінійну систему і вирішуйте.

Доларів$7,000$ основної суми інвестується в два рахунки, один заробляє$3$% відсотків, а інший заробляє$7$% відсотків. Якщо сумарні відсотки за рік складають $$262$, то скільки вкладено в кожен рахунок?
Мері має загальну економію $$12,500$ на двох різних рахунках компакт-дисків. Один компакт-диск заробляє$4.4$% відсотків, а інший заробляє$3.2$% відсотків. Якщо її сумарний відсоток за рік становить $$463$, то скільки у неї на кожному CD-рахунку?
Sally $$1,800$ заощадження знаходиться на двох рахунках. Один рахунок заробляє$6$% річних відсотків, а інший заробляє$3$%. Її загальний відсоток за рік становить $$93$. Скільки у неї в кожному обліковому записі?
Джо має два ощадні рахунки на загальну суму $$4,500$. Один рахунок заробляє$3\frac{3}{4}$% річних відсотків, а інший заробляє$2\frac{5}{8}$%. Якщо його сумарний відсоток за рік становить $$141.75$, то скільки коштує на кожному рахунку?
Millicent$10,000$ інвестував $ на два рахунки. За рік вона заробляє на $$535$ більше відсотків зі свого$7$% пайового фонду, ніж зі свого$4$% CD. Скільки у неї в кожному обліковому записі?
Малий бізнес$85,000$ інвестував $ на два рахунки. Якщо рахунок заробляє$3$% річних відсотків заробляє $$825$ більше відсотків, ніж рахунок заробляє$4.5$% річних відсотків, то скільки вкладається в кожен рахунок?
Джеррі заробив в цілому $$284$ в простих відсотках з двох окремих рахунків. На рахунок, який заробляє$6$% відсотків, Джеррі вклав $$1,000$ більш ніж в два рази більше суми, яку він вклав в рахунок, заробляючи$4$%. Скільки він вклав в кожен рахунок?
Джеймс заробив загальну суму $$68.25$ в простих відсотках з двох окремих рахунків. На рахунок, який заробляє$2.6$% відсотків, Джеймс вклав половину стільки ж, скільки він зробив на іншому рахунку, який заробив$5.2$%. Скільки він вклав в кожен рахунок?
Касовий апарат містить$10$ купюри $ і $$20$ купюри загальною вартістю $$340$. Якщо є$23$ купюри загальні, то скільки кожного містить реєстр?
Джон зміг придбати піцу за $$10.80$ з чвертями і копійками. Якщо він використовує$60$ монети, щоб купити піцу, то скільки з них у нього було?
Денніс скосив сусідський газон для баночки з копійками і нікелями. Завершивши завдання, він порахував монети і виявив, що їх було$4$ менше, ніж в два рази більше копійок, ніж нікелів. Загальна вартість всіх монет - $$6.60$. Скільки у нього було кожної монети?
Дві сім'ї купили квитки на великий футбольний матч. Одна сім'я замовила$2$ дорослі квитки та$3$ дитячі квитки на загальну суму $$26.00$. Інша сім'я замовила$3$ дорослі квитки і$4$ дитячі квитки на загальну суму $$37.00$. Скільки коштував кожен дорослий квиток?
Двоє друзів знайшли сорочки та шорти у продажу на блошиному ринку. Один купив$5$ сорочки та$3$ шорти на загальну суму $$51.00$. Інший купив$3$ сорочки та$7$ шорти на загальну суму $$80.00$. Скільки коштувала кожна сорочка і кожна пара шортів?
У понеділок Джо купив$10$ чашки кави і$5$ пончики для свого офісу за ціною $$16.50$. Виявляється, пончики були більш популярними, ніж кава. Тому у вівторок він купив$5$ чашки кави і$10$ пончики на загальну суму $$14.25$. Скільки коштувала кожна чашка кави?

Відповідь

1. $$5,700$$3$ в% і $$1,300$ при$7$%

3. $$1,300$$6$ в% і $$500$ при$3$%

5. $$8,500$$7$ в% і $$1,500$ при$4$%

7. $$1,400$$4$ в% і $$3,800$ при$6$%

9. $12$десятки і$11$ двадцяті

11. $52$копійки і$28$ нікельси

13. Сорочки: $$4.50$; шорти: $$9.50$

Вправа$\PageIndex{7}$ Mixture Problems

Налаштуйте лінійну систему і вирішуйте.

$15$% розчин кислоти повинен бути змішаний з$25$% -ним розчином кислоти для отримання$12$ галонів$20$% розчину кислоти. Скільки потрібно кожного?
Один спиртовий розчин містить$12$% спирту, а інший містить$26$% спирту. Скільки з кожного слід змішати разом, щоб отримати$5$ галони$14.8$% спиртового розчину?
Медсестра бажає отримати$40$ унції сольового розчину$1.2$%. Скільки$1$% сольового розчину вона повинна змішати з$2$% сольовим розчином для досягнення бажаного результату?
Клієнт замовив$20$ фунти добрив, що містить$15$% азоту. Щоб заповнити замовлення замовника, скільки$30$ запасів азотних добрив потрібно змішати з$10$% азотних добрив?
Клієнт замовив$2$ фунти змішаного арахісового продукту, що містить$15$% кешью. Інвентар складається лише з двох сумішей, що містять$10$$30$% і% кешью. Скільки кожного типу потрібно змішати, щоб заповнити замовлення?
Скільки фунтів чистого арахісу потрібно поєднувати$20$ з% арахісовою сумішшю, щоб$10$ отримати фунти арахісової суміші$32$%?
Скільки чистячої рідини з$20$% вмістом спирту, необхідно змішати з водою, щоб отримати суміш$24$ -унція$10$ з% вмістом спирту?
Хімік бажає створити розчин$32$ -унція з вмістом кислоти$12$%. Він використовує два типи вихідних розчинів, один з вмістом кислоти$30$%, а інший з вмістом кислоти$10$%. Скільки кожного йому потрібно?
Концентрований миючий розчин, що містить$50$% аміаку, змішують з іншим розчином, що містить$10$% аміаку. Скільки з кожного змішується, щоб отримати$8$ унції формули очищення аміаку$32$%?
$50$% концентрат фруктового соку можна придбати оптом. Кращий смак досягається при змішуванні води з концентратом таким чином, щоб отримати$12$% суміші фруктових соків. Скільки води і концентрату потрібно для приготування фруктового напою$50$ -унція?
$75$% концентрат антифризу змішують з водою для отримання$6$ галонів$25$% розчину антифризу. Скільки потрібно води?
Чистий цукор повинен бути змішаний з фруктовим салатом, що містить$10$% цукру для отримання$48$ унцій салату, що містить$16$% цукру. Скільки потрібно чистого цукру?

Відповідь

1. $6$галонів кожного

3. $32$унції$1$% сольового розчину і$8$ унції$2$% сольового розчину

5. $1.5$фунти$10$ змішування% кешью та$0.5$ фунтів суміші кешью$30$%

7. $12$унцій чистячої рідини

9. $4.4$унції$50$% розчину аміаку і$3.6$ унції$10$% розчину аміаку

11. $4$галонів

Вправа$\PageIndex{8}$ Uniform Motion Problems

Налаштуйте лінійну систему і вирішуйте.

Літак в середньому$460$ милі на годину в поїздці з вітром за ним і$345$ милями на годину на зворотній поїздці проти вітру. Якщо загальна поїздка туди і назад зайняла$7$ години, то скільки часу літак витратив на кожен відрізок поїздки?
Дві ноги$330$ -милі поїздки зайняли$5$ години. Середня швидкість для першого етапу поїздки становила$70$ милі на годину, а середня швидкість для другого етапу поїздки склала$60$ милі на годину. Скільки часу займала кожна нога поїздки?
Виконавчий подорожував$1,200$ милями, частина на вертольоті і частина на приватному літаку. Реактивний літак в середньому$320$ милі на годину в той час як вертоліт в середньому$80$ милі на годину. Якщо загальна поїздка зайняла$4\frac{1}{2}$ години, то скільки часу вона провела в приватному літаку?
Джо взяв два автобуси на$463$ -мильну поїздку від Сан-Хосе до Сан-Дієго. Перший автобус усереднював$50$ милі на годину, а другий автобус зміг усереднити$64$ милі на годину. Якщо загальна поїздка зайняла$8$ години, то скільки часу було проведено в кожному автобусі?
Біллі катався на каное вниз за течією до загального магазину із середньою швидкістю$9$ миль на годину. Його середня швидкість катання на каное назад вгору за течією становила$4$ милі на годину. Якщо загальна поїздка зайняла$6\frac{1}{2}$ години, то скільки часу знадобилося Біллі, щоб повернутися в зворотну поїздку?
Два брати проїхали$2,793$ кілометри від Лос-Анджелеса до Нью-Йорка. Один з братів, проїжджаючи вдень, зміг скласти середні$70$ кілометри на годину, а інший, проїжджаючи вночі, зміг усереднити$53$ кілометри на годину. Якщо загальна поїздка зайняла$45$ години, то скільки годин керував кожен брат?
Човен проїхав$24$ милі вниз за течією за$2$ годинами. Поїздка назад зайняла в два рази більше часу. Якою була швидкість човна і течія?
Вертоліт, що летить з вітром, може проїхати$525$ милі за$5$ годинами. На зворотну поїздку, проти вітру, піде$7$ години. Які швидкості вертольота і вітру?
Човен може проїхати$42$ милі з течією нижче за течією за$3$ годинами. Повертаючись вгору за течією проти течії, човен може проїхати лише$33$ милі за$3$ годинами. Знайти швидкість струму.
Легкий літак, що летить з вітром, може проїхати$180$ милі за$1\frac{1}{2}$ годинами. Літак може пролетіти однакову відстань проти вітру за$2$ годинами. Знайти швидкість вітру.

Відповідь

1. Літак летів$3$ годинами з вітром і$4$ годинами проти вітру.

3. $3.5$годин

5. $4.5$годин

7. Човен:$9$ милі на годину; струм:$3$ милі на годину

9. $1.5$миль на годину

Вправа$\PageIndex{9}$ Discussion Board

Складіть числову або грошову задачу, яку можна вирішити за допомогою власної системи рівнянь і поділіться нею на дошці обговорень.
Складіть задачу суміші, яку можна вирішити за допомогою власної системи рівнянь і поділіться нею на дошці обговорень.
Складіть задачу рівномірного руху, яку можна вирішити за допомогою власної системи рівнянь і поділіться нею на дискусійній дошці

Відповідь

1. Відповіді можуть відрізнятися

3. Відповіді можуть відрізнятися

	Відсоток	Сума
Сіль	\(2\)%\(=0.02\)	\(0.02(20\)унцій)\(=0.4\) унцій
Вода	\(98\)%\(=0.98\)	\(0.98(20\)унцій)\(=19.6\) унцій